高扬程两级双吸离心泵时序效应研究

叶长亮，王福军，2，李怀成，李震昙，宋青松

（1.中国农业大学 水利与土木工程学院，北京 100083；2.北京市供水管网系统安全与节能工程技术研究中心，北京 100083；3.上海连成集团有限公司，上海 201812）

1 研究背景

双进口两级双吸离心泵为两侧吸入中间压出，分布在左右两侧对称布置的首级叶轮为单吸式，中间的第二级叶轮为双吸式，首级与第二级叶轮之间采用过渡流道连接。该泵不但继承了双吸离心泵流量大的特点，还突出了高扬程的特点，目前被长距离调水工程、高扬程灌溉提水工程所广泛采用［1-2］。如云南省玉溪三湖生态保护水资源配置工程、山西夹马口引黄工程和西范引黄工程等均采用了这种泵型，单泵扬程均在150 m以上。

在对多级泵进行装配时，第一级叶轮与导叶之间、导叶与第二级叶轮之间，以及后续类似组合都存在周向相对位置问题，当各个相位角发生改变时，水泵的性能也会随之发生变化，这一现象被称为时序效应。国内外学者在涡轮、压缩机等领域对时序效应进行了较广泛研究。BEHR等［3］针对一台高压涡轮的动叶与动叶和静叶与静叶的时序效应进行了试验研究，结果表明时序效应对效率有一定的影响，原因在于，调整动叶片的周向位置会导致上游叶片所产生的尾迹冲击到下游叶片，从而对下游动叶片的气动性能产生影响。BOHN等［4］采用数值模拟方法对一台两级轴流透平的第二个静叶时序位置进行了优化，得到了一个效率最高的静叶时序位置。

相对于气力机械而言，水力机械中水的黏性较大，上游部件尾缘更易形成较大尾迹涡［5］，在其进入下游部件后，进一步发展、混合，形成新的漩涡，从而影响下游部件水力性能，引起水压脉动。对于单级离心泵而言，现有的研究以导叶与蜗壳之间的时序效应为主，刘厚林等［6］研究了导叶与隔舌不同时序位置时对泵扬程、效率的影响，Jiang等［7］分析了导叶不同时序位置对离心泵内隔舌处压力脉动和叶轮径向力等非定常特性的影响。Wang等［8］对一台环形蜗壳离心泵的时序效应展开CFD分析，结果表明，时序效应对叶轮与导叶动静干涉引起的压力脉动影响较大，对蜗壳的压力脉动强度影响较为明显。Tan等［9］研究了五级节段式离心泵首级叶轮与第二级叶轮之间的时序效应，采用了叶轮相位不交错，对称交错，只交错第一级叶轮以及只交错后两级叶轮的几种方案，测试了多级泵干涉较为强烈首级叶轮出口和第二级叶轮出口的压力脉动，通过采用SSTk-ω数值模拟得到对称交错对于压力脉动改善较为明显。

双进口两级双吸离心泵相较于普通多级泵而言，第二级叶轮为双吸叶轮，双吸叶轮与单吸叶轮由于结构上的差异必将导致不同的时序效应。目前对双进口两级双吸离心泵时序效应的研究还是空白，对如何旋转两级叶轮的相对位置还缺少科学依据。为此，本文针对一台黄河沿岸提水灌溉泵站普遍使用的两级双吸离心泵，通过试验研究和数值计算相结合的手段，分析4种不同相位角方案下的时序效应问题，提出这类泵型的最优相位编排方案。

2 计算模型

2.1 研究对象本文研究对象是山西西范灌区引黄工程一级泵站所采用的双进口两级双吸离心泵，主要参数见表1。

数值模拟的计算域包括两侧的吸水室、首级单吸叶轮和过渡流道以及第二级双吸叶轮和压水室部分。为使得到稳定的流场，对两侧吸水室进口和压水室出口从法兰处分别延长进出口直径的2倍。整体计算域如图1所示。

图1 两级双吸离心泵整体计算域

表1 离心泵参数

2.2 网格划分与数值方法网格划分是数值模拟中较为关键的一步，网格的质量的好坏直接影响着计算精度。相比结构网格，非结构化网格生成速度快，对于复杂结构的几何模型具有良好的适用性［10-11］，考虑到双进口两级双吸离心泵结构的复杂性，因此本文采用ICEM软件对离心泵进行全流场非结构网格划分，并对壁面进行边界层加密。采用SSTk-ω湍流模型进行数值计算，该模型及算法对于旋转流动、强逆压梯度的边界层流动、流动分离和二次流均具有很好的流动线形［12-13］。离散格式采用高阶，在进水管进口设置总压进口边界条件，在出水管出口设置质量流量边界条件。定常计算动静交界面采用冻结转子法［14］，近壁区采用适应性较好的automatic函数［15］。对数值模拟进行网格无关性检查［16-17］，如图2所示，最终确定网格数约为643万。

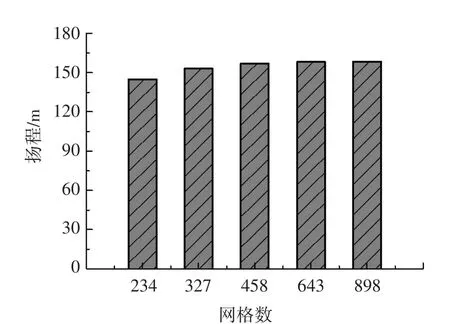
图2 网格无关性分析（×104）

以定常计算结果作为非定常计算的初始条件，叶轮与其相邻过流部件的交界面设置为瞬态冻结转子。时间步长为2.222×10-4s，即叶轮旋转1°的时间，计算得出库朗数小于20，收敛性和稳定性较好。叶轮旋转10个周期，选取第10个周期的结果用于分析。

2.3 叶轮相位与监测点布置根据时序位置的不同，本文定义了4种方案，分别为：（1）周向位置一字型排列，相位角为0°；（2）首级叶轮与第二级叶轮交错15°；（3）首级叶轮与第二级叶轮对称交错，相位角为30°；（4）首级叶轮与第二级叶轮交错45°。4种方案如图3所示。

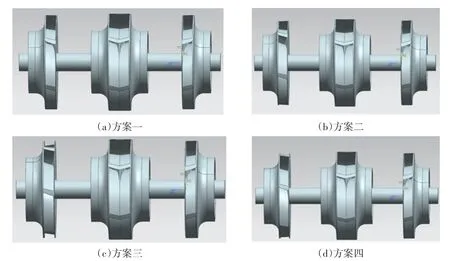
图3 4种方案下的叶轮相对周向位置

为监测离心泵内部压力脉动情况，设置的监测点如图4所示。监测点1位于吸水室隔舌处附近（图4（a））。监测点2、3、4分别位于过渡流道入口隔舌处、流道外径最大处以及流道出口处（图4（b））；监测点5、6位于过渡流道桥接流道的进出口处（图4（c））；监测点7、8、9位于过渡流道反流道的进口处（图4（d）），最大转弯处以及出口处。监测点10、11、13分别位于压水室隔舌处、最高处、以及出口处（图4（e））。

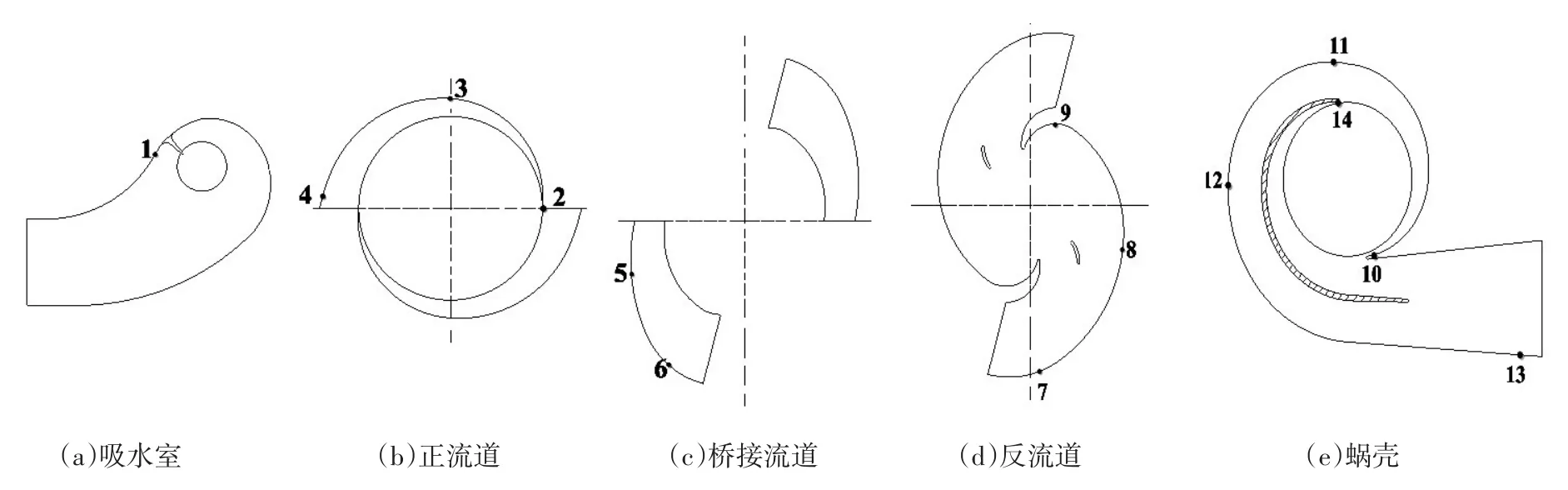
图4 压力脉动监测点的分布

为了直观反映压力脉动的幅度，以便进行不同对象或不同位置间压力脉动大小的比较，本文引入压力系数Cp这一参数。常用的压力系数计算公式［18-19］如公式（1）所示，式中Δp为压力与其平均值之差，u为叶轮出口圆周速度，ρ为流体密度，D为叶轮出口直径，n为离心泵额定转速，对于泵的第一级和第二级，压力系数的分母值将根据其不同的叶轮出口直径分别计算。

在CFD计算中，径向力计算式［20-21］如下，F为径向力合力，Fx与Fy分别表示x、y方向径向力，A1与A2分别表示叶轮进、出口过流面积，Vr为叶轮某一节点处流体质点的径向速度，Vx与Vy分别表示x、y方向分速度，ω为旋转角速度，θ为流体质点初始角度，t为时间，ρ为流体密度，p压力。式中右边前两项表示叶轮内的动量通量；第三项表示叶轮内部流体动量变化引起的力，最后一项表示叶轮出口产生的压力，由于叶轮进口垂直于主轴，因此产生的力被忽略。

3 外特性分析

为了给数值计算提供依据，对所研究的双进口两级双吸离心泵进行了外特性试验研究，试验是在上海连成集团有限公司水泵试验台进行。试验系统回路见图5，包括循环水池、试验用双进口两级双吸离心泵、泵入口管线、泵出口管线、压力传感器、流量计、调节阀，以及其它检测、记录、分析、控制等辅助系统。试验台上安装的两级双吸离心泵见图6。该试验装置综合测量误差为±0.5%。

图7给出了叶轮周向位置一字型排列，即相位角为0°时，水泵外特性曲线的数值模拟与试验结果对比。在额定工况上，数值计算扬程为158.72 m，试验扬程为161.41 m，扬程数值计算与试验相对误差为1.7%；数值计算效率为86.2%，试验效率为88.03%，效率数值计算与试验相对误差为2.1%。据此结果可以认为，数值模拟值与试验结果基本一致，数值计算结果有较高可信度。

图6 测试用的双进口两级双吸离心泵

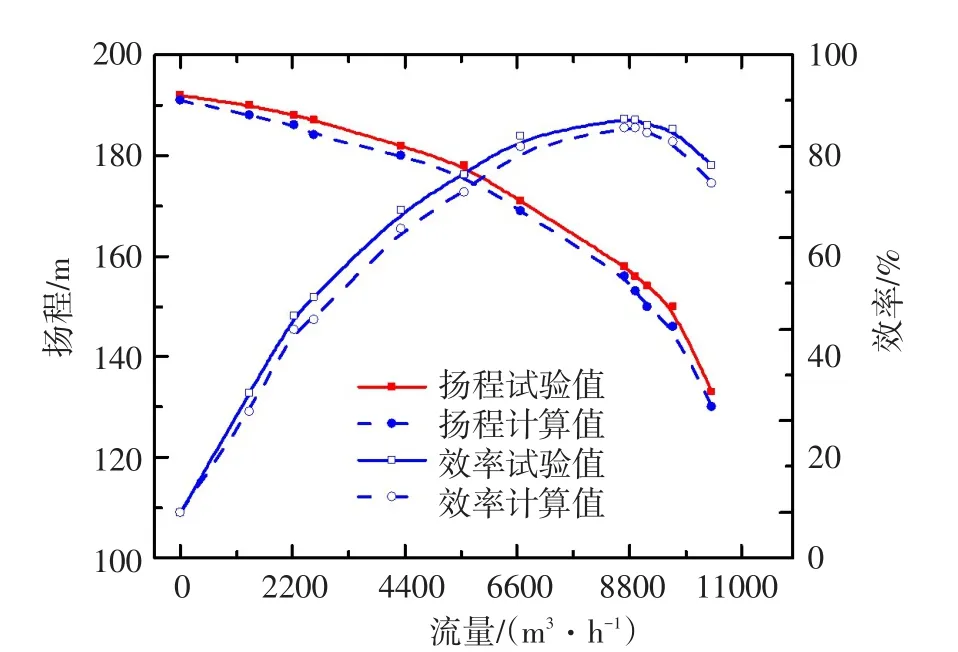
图7 方案一泵性能曲线试验与模拟对比

图8给出了数值计算得出的4种方案下水泵扬程-流量关系曲线和水泵效率-流量关系曲线。从图中可以看出，4种方案下的扬程和效率相差并不大，其中在设计工况下，4种方案对应的扬程分别为158.72、159.31、160.82和159.27 m；4种方案对应的效率分别为86.20%、86.43%、87.03%和86.29%；设计工况下方案三对应的扬程最高，该方案比方案一、二、四的扬程分别高0.96%、0.95%和1%。设计工况下方案三对应的效率最高，该方案比方案一、二、四的效率分别高0.96%、0.95%和1%。该结果说明不同方案的外特性整体趋势一致，数值差别不大。

图8 4种方案下水泵外特性计算结果对比

4 压力脉动特性分析

4.1 吸水室压力脉动特性分析通过对吸水室各个部位的压力脉动进行对比分析发现，隔舌附近区域为吸水室压力脉动最大区域，图9给出了设计工况下4种方案对应的吸水室隔舌处监测点压力脉动主频分布情况。可以看出，4种方案下的主频均为1倍叶频（75 Hz），主频幅值分别为0.017、0.018、0.015和0.017，变化率在5%以内，这说明叶轮相位对吸水室压力脉动的影响不明显。

图9 设计工况下监测点1压力脉动频域

4.2 过渡流道压力脉动特性分析选取过渡流道入口隔舌处、流道外径最大处以及流道出口处3个位置的监测点，对4种方案设计工况下的压力脉动特性进行分析发现，监测点主频发生了一定变化，但均为叶频的倍数。图10可以看出，叶轮相位对正流道内压力脉动特性产生了影响，其中在过渡流道隔舌处相对明显。4种方案下脉动主频幅值分别为0.054、0.02645、0.01675和0.02742；方案三对应的脉动主频幅值最小，比方案一、二、四分别小69%、37%和39%。

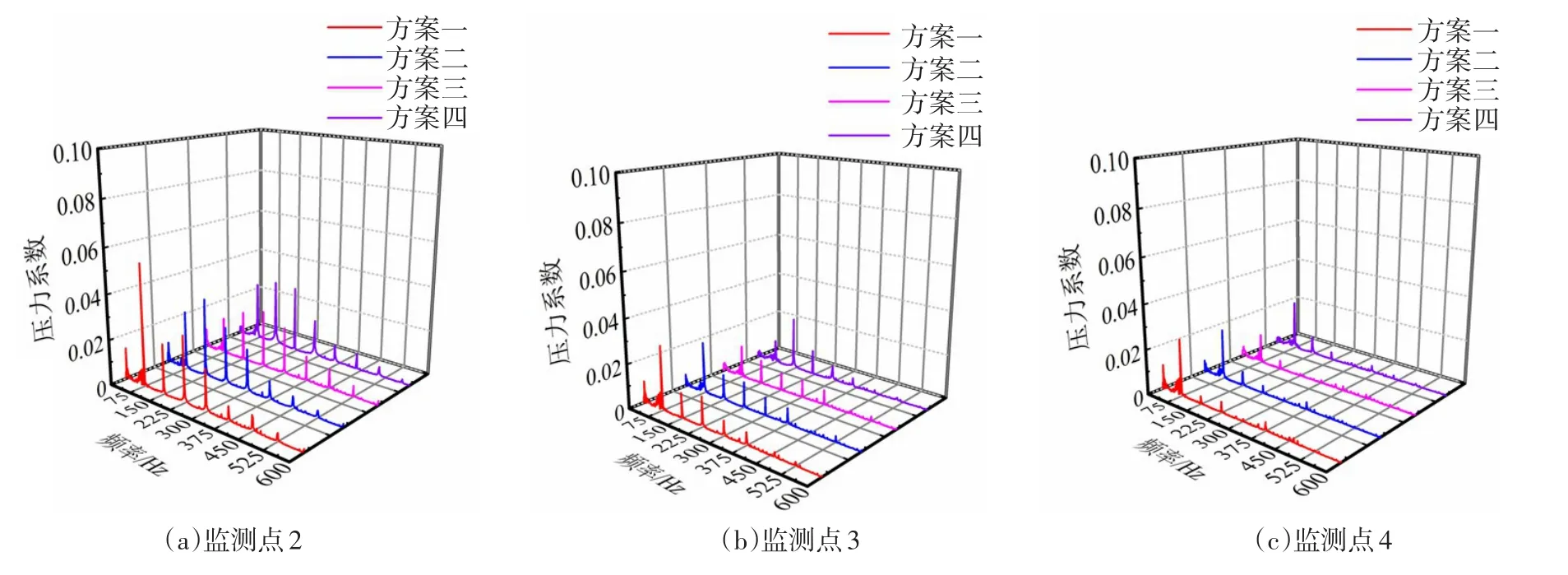
图10 设计工况下正流道监测点压力脉动频域

压力脉动的本质为压力随时间的变化，因此压力的变化能直观地反映叶轮相位对压力脉动的影响。设计工况下同一时刻首级叶轮出口静压分布如图11所示。可以看到，截面内的压力分布受叶轮相位的影响较大。方案二、四压力分布不均匀，压力梯度也相对较大。这主要是由于叶轮位置的变化导致从叶轮流出的液流方向发生了改变，液流在隔舌部位与壁面发生剧烈撞击形成漩涡，从而导致截面内压力分布不均匀，形成较大的压力梯度。

图11 设计工况下首级叶轮出口静压分布

过渡流道正流道隔舌处受到动静干涉影响较大，进一步对比4种方案该位置在3种典型工况下的压力脉动特性，如图12所示。4种方案的主频幅值都表现出在小流量工况下最大，设计工况下最小的特点。叶轮相位的改变对于该位置处压力脉动影响在小流量工况下更为显著，4种方案对应脉动的主频幅值分别为0.0743、0.04477、0.03374和0.04264。其中，方案三对应的主频脉动幅值分别比方案一、二、四低55%、22%、21%。

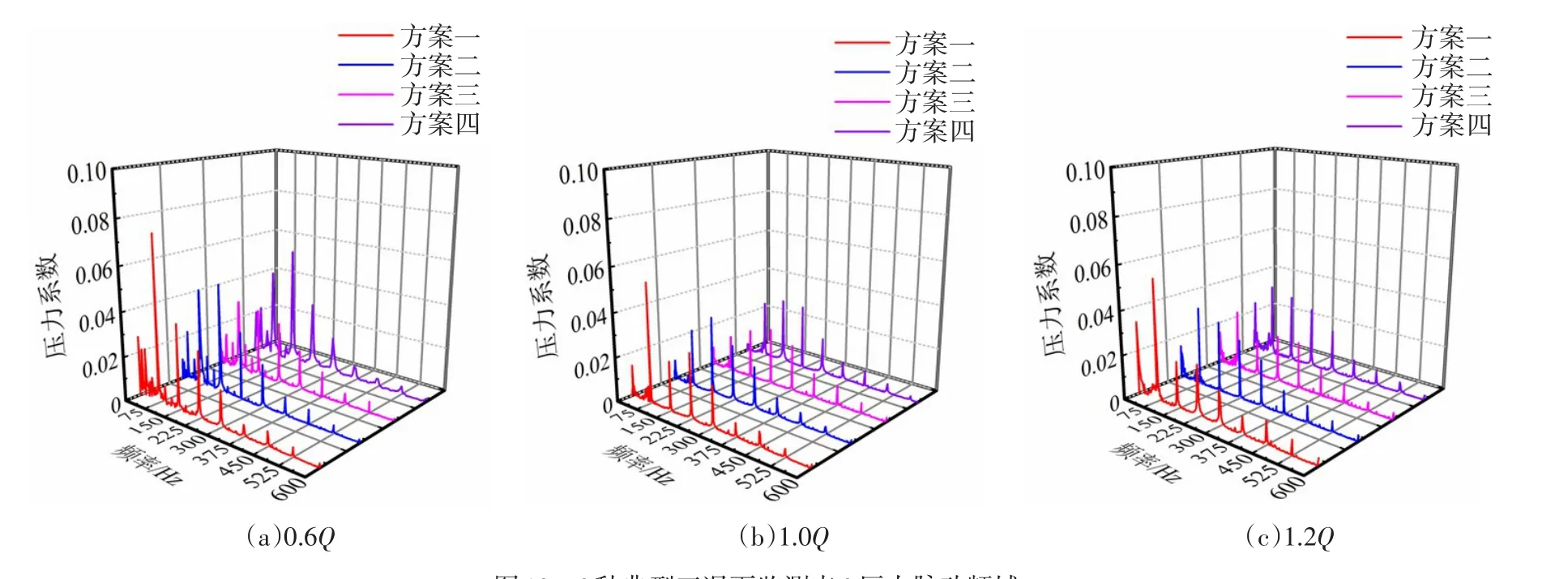
图12 3种典型工况下监测点2压力脉动频域

射流-尾迹结构能较好的体现叶片出口边的流态。设计工况下4种方案首级叶轮出口边的相对速度分布如图13所示。分析可知，4种方案首级叶轮的出口边射流-尾迹结构明显，4种方案最大相对速度分别为30、29、23.5和34.2 m/s。相比于方案一、二、四，方案三首级叶轮出口边相对速度的变化幅度明显较小，表明方案三对叶轮的速度三角形有影响，对于二次流有一定的改善作用。

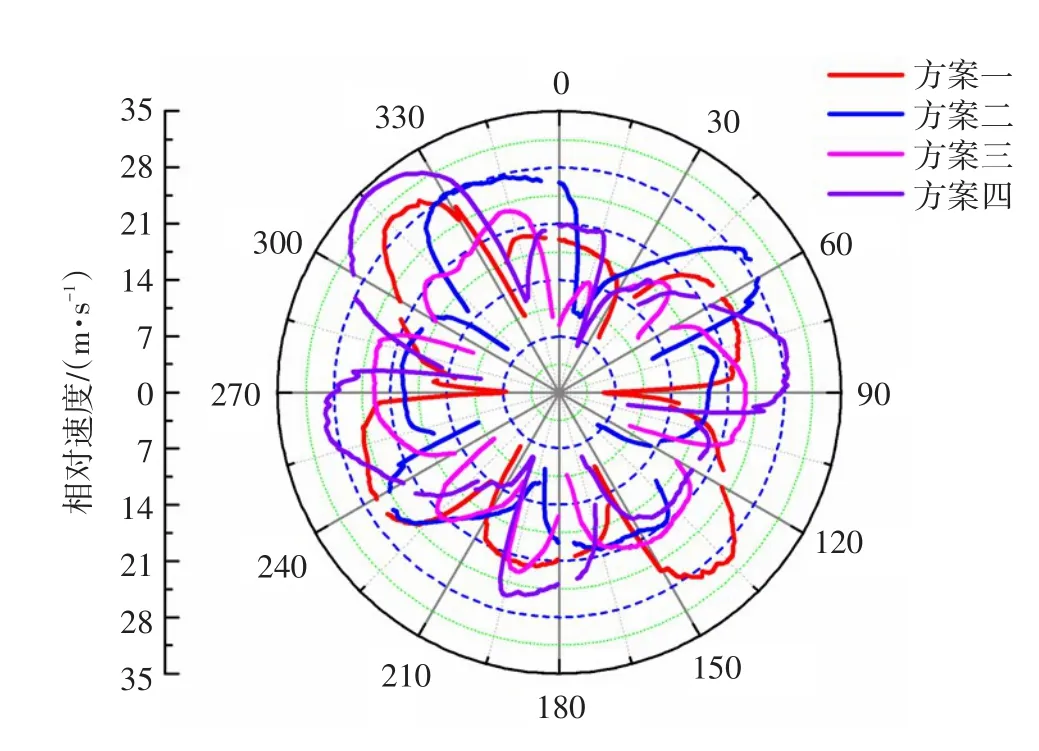
图13 设计工况下4种方案叶轮出口圆周速度分布

图14（a）为设计工况下桥接流道内进口监测点5的压力脉动频域图，可以看出，叶轮相位的改变影响了桥接流道内的压力脉动主频幅值。在桥接流道进口处，4种方案对应脉动主频幅值分别为0.02406、002198、0.01405、0.02205。方案三脉动的主频幅值分别比方案一、二、四要小42%，33%和36%。图14（b）为设计工况下反流道内出口监测点9的压力脉动频域图。4种方案下反流道内主频未发生变化，均为一倍叶频（75Hz）。叶轮相位的改变影响了反流道内压力脉动主频幅值，在反流道出口处，4种方案对应的主频幅值分别为0.02017、0.02048、0.01334和0.0193。其中，方案三对应的主频脉动幅值分别比方案一、二、四要小34%、35%和33%。

图14 设计工况下监测点压力脉动频域图

进一步观察4种方案在设计工况下反流道内的流态，如图15所示。反流道为双螺旋结构，由于桥接流道空间扭曲，因此水流流经桥接流道进入反流道出现一定的漩涡。4种方案均存在漩涡并伴随明显的低速区，其中，4种方案下反流道在同一时刻的小于6 m/s的低速区占比分别为48%、45%、35%及38%；方案一、二在进口处出现了明显的漩涡区，方案三、四进口处漩涡区较小；这说明叶轮相位的变化对于反流道的流态影响较大，进而对压力脉动产生影响。通过对过渡流道正流道，反流道以及桥接流道的压力脉动研究可以发现，时序效应对过渡流道压力脉动影响较大。

4.3 压水室压力脉动特性分析图16为3种典型工况4种方案的压水室隔舌处的压力脉动频域图，可以看出，4种方案该区域脉动主频幅值都表现出在小流量工况下最大，设计工况下最小的特点。叶轮相位的改变对于该位置处压力脉动影响在小流量工况下更为显著，4种方案对应脉动的主频幅值分别为0.0743、0.04477、0.03374和0.04264。其中，方案三对应的主频脉动幅值分别比方案一、二、四减小50%、33%和40%。

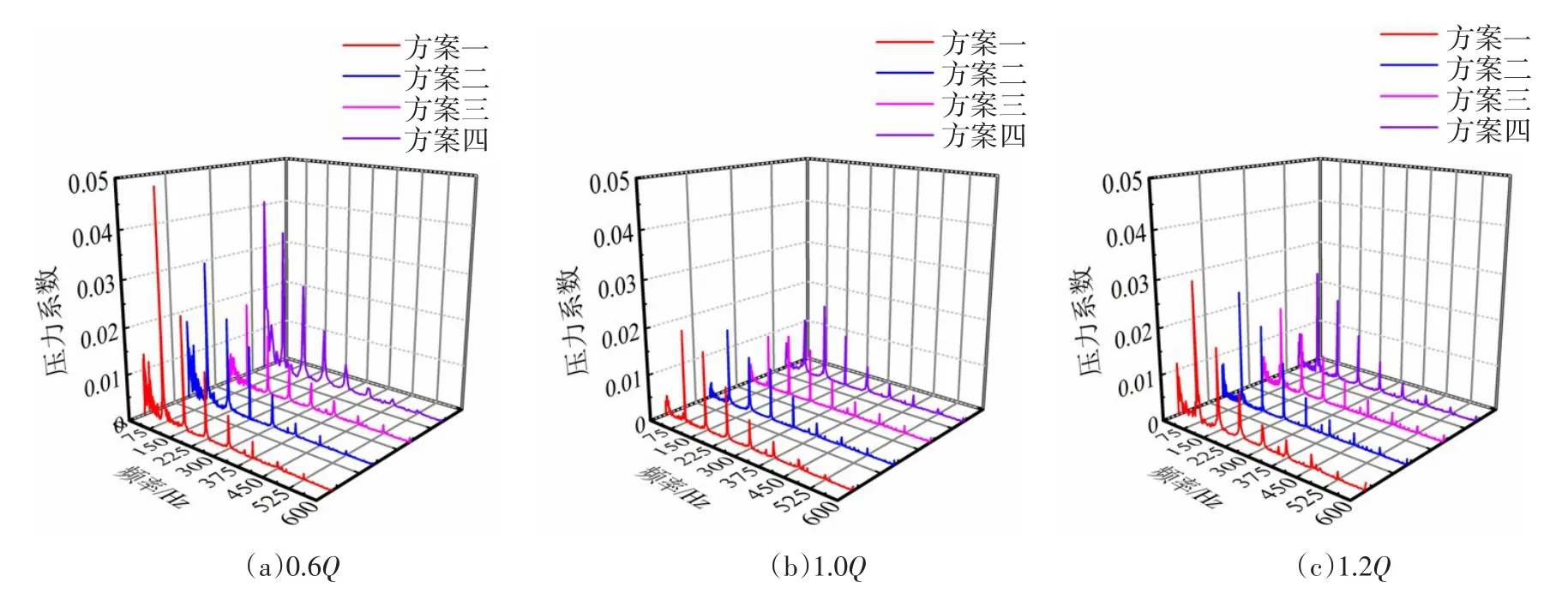
图16 3种典型工况下监测点10压力脉动频域图

设计工况下第二级叶轮出口处静压分布如图17所示，可以发现4种方案叶轮出口都存在明显的射流-尾迹的流动现象，由于采用双吸叶轮，叶轮出口流动具有明显的对称性。由于压水室隔舌的压力脉动受射流-尾迹的影响，又存在动静干涉的作用，压力脉动能量幅值较大；相较方案一、二、四，方案三叶轮出口压力梯度相对较小，因此对应压力脉动的主频幅值也较小。

图17 设计工况下第二级叶轮出口静压分布

5 径向力特性分析

图18为3种典型工况下作用在首级叶轮径向力矢量分布，图中某一点的矢量坐标代表某一时刻径向力的大小和方向。可以看出，不同工况下，4种方案叶轮上所受径向力分布相似，叶轮所受径向力分布周期性均很明显，周期与叶片数有关且呈近似六角形分布。在叶轮一个旋转周期内，不同工况下叶轮上所受径向力大小和方向随时间变化而发生变化；设计工况和大流量工况下，叶轮所受径向力方向均匀分布在4个象限，小流量工况下叶轮所受到径向力变化剧烈，这可能是由于小流量工况下，叶片与隔舌之间的动静干涉作用增强。

图18 3种典型工况下首级叶轮径向力矢量分布

矢量力反映受力方向和力的变化分布范围，采用极坐标能直观反映径向力的大小。图19为3种典型工况下首级叶轮径向力大小分布。通过对径向力绝对值大小分析发现，4种方案对应的首级叶轮径向力均在设计工况下最小，小流量工况下最大。在小流量与大流量工况下，3种工况下方案三在4个象限分布的均匀性较好且径向力较小。

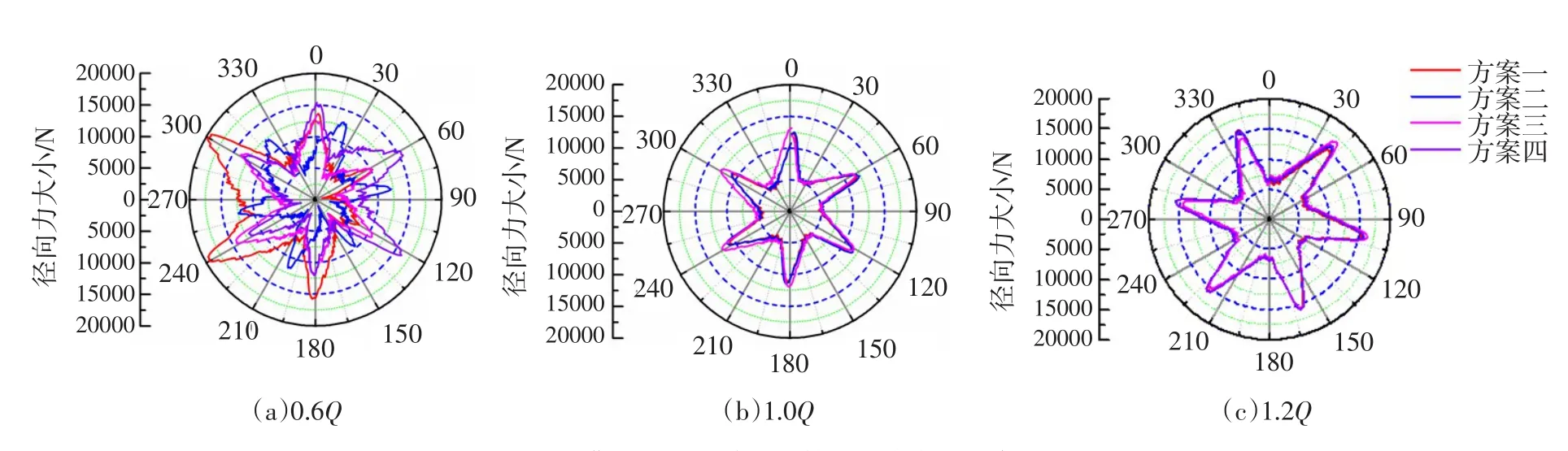
图19 3种典型工况下首级叶轮径向力大小分布

图20为3种典型工况下第二级叶轮径向力矢量分布图，可以看出相较于首级叶轮，第二级叶轮的径向力分布规律性较差，这与水流经过过渡流道后的流态变差有关。3种工况下，在一个旋转周期内，4种方案的第二级叶轮所受径向力的大小和方向随时间而发生剧烈变化；4种方案的第二级叶轮径向力都表现为设计工况下最小；其中方案三对应的第二级叶轮在4个象限分布的均匀性较好且径向力较小。通过对离心泵的两级叶轮径向力分析，可以看出，叶轮相位的变化影响两级叶轮的径向力特性。

叶轮出口处压力分布的不稳定会引起径向力的产生，旋转叶轮内的流动不对称造成径向力不平衡。结合图21可以发现叶轮出口处存在射流-尾迹的流动现象。这种现象使随时间变化的动态径向力会让水力机械内部流动变得不稳定。内部流动的不对称主要是由于叶片与正流道的水力作用明显，由于动静干涉对叶轮内部区域的流动产生明显的扰动，使叶轮内部流场出现不对称的现象，作用在叶轮叶片上的压力不均匀、不对称，导致在非定常条件下叶轮受的径向力出现不稳定的变化。方案

图20 3种典型工况下第二级叶轮径向力矢量分布

三叶片出口的静压分布要相对均匀，压力梯度较小，这说明叶轮相位影响了叶轮出口流动的均匀性进而影响了径向力的大小。

图21 设计工况下正流道中截面静压分布

6 结论

本文采用SSTk-ω湍流模型针对一台两级叶轮均为6叶片的双进口两级双吸离心泵时序效应特性进行了研究，详细分析了相位分别为0°、15°、30°及45°等4种方案下的泵内压力脉动特性和径向力变化情况，得出以下结论。

（1）时序效应对离心泵外特性影响较小，不同叶轮相位对应的效率和扬程之间差距小于2%。

（2）时序效应对离心泵压力脉动特性有较明显影响，对过渡流道和压水室的影响大于其他部位。在过渡流道的正流道隔舌处，30°方案下的脉动主频幅值分别比0°、15°、45°方案减少70%、38%和40%。在压水室隔舌处，30°方案下的脉动主频幅值分别比0°、15°、45°减少31%、18%和22%。叶轮相位的变化使从叶轮流出的液流方向发生了改变，从而导致泵内压力分布产生变化进而影响泵内压力脉动特性。

（3）时序效应对离心泵径向力有较大影响。4种方案下离心泵径向力均呈周期性变化规律，即六角形分布，且径向力的大小和方向随时间的变化而变化。3种工况下，30°方案的动静干涉对叶轮内部区域的流动扰动影响最小，叶轮内部流场比较对称，作用在叶轮叶片上的压力相对均匀，叶轮所受到径向力最小。

综合考虑压力脉动和径向力两项非定常指标，建议首级叶轮相对于第二级叶轮对称交错布置，更有利于双进口两级双吸泵的稳定运行。