梯形河道行洪能力与护岸糙率的关系研究

左 静

（临沂市兰山区水务局,山东 临沂 276000）

在评估河道行洪能力和输水能力时,河道阻力是需要考虑的首要问题,在河道水力计算中,常用河道糙率作为反映河道阻力的综合性系数,客观准确的河道糙率是河道安全运行的关键因素。

由于天然河道有植被覆盖,影响河道水力计算。因此国内外相关学者对河道植被的阻水特性进行了大量的研究。Luhar 等[1]研究了曼宁糙率系数在不同河道植被情况下的变化规律。Aberle 等[2]研究了不同河道断面非淹没植被的阻力特性,随着国内河道生态治理的不断深入,含植被河道和生态护岸等效糙率越来越受到学者的重视,韩丽娟等[3]指出漂浮植被会对河道的综合阻力系数产生影响；孙东坡[4]等对新型生态防洪护面连锁块的力学稳定性和抗冲性进行了研究,指出混凝土生态护面具有改善河道生态环境的作用,并得出该结构的糙率与流速之间的关系。郑爽[5]等人对淹没植物的挺立度,相对淹没高度和相对密度与曼宁糙率系数的关系,给出了等效曼宁糙率系数经验公式；吴乔枫等[6]根据植被空间上分布的差异性和河道流量情况对河道断面进行分区,提出了河道综合糙率计算公式。

梯形河道的行洪能力会受到岸坡类型的影响,岸坡类型直接影响河道阻力及水流结构,因此,研究护岸糙率特性及其对河道行洪能力的影响是十分必要的。通过室内实验和数值仿真,对梯形断面河道中各种护坡的糙率变化规律进行研究,并对其影响因素进行分析。

1 试验概况

试验在矩形变坡循环水槽中进行（长×宽×高=20 m×1.2 m×0.7 m）,进口采用稳流装置,确保进水顺畅,出水口采用栅栏式尾门,通过阀门和电磁流量计进行流量调节。梯形截面采用有机玻璃片设置,长度12 m。主槽的宽度是0.8 m,渠道坡度为1∶1,高度0.4 m,见图1。本研究中的生态护岸是由8 mm 的仿生草皮与MMA 材质的三棱柱砖块组成,用来模拟天然河道对水流的影响效果。实验共设置3 种不同大小的砖块,每种砖块的迎水面与底面的夹角为15°（护岸A）、30°（护岸B）和45°（护岸C）。砖的纵向间隔为0.4 m,横向间隔为0.05 m。

对各护岸采用不同流量和不同底坡进行试验,得到其对应的均匀流水深（对各断面水深进行测量,当断面水深差小于1mm 时,即可视为均匀流）,试验结果见表1 。Q 是流量,i 是底坡，护岸A 对应A1~A8,护岸 B 对应B1~B8，护岸C 对应C1~C8。

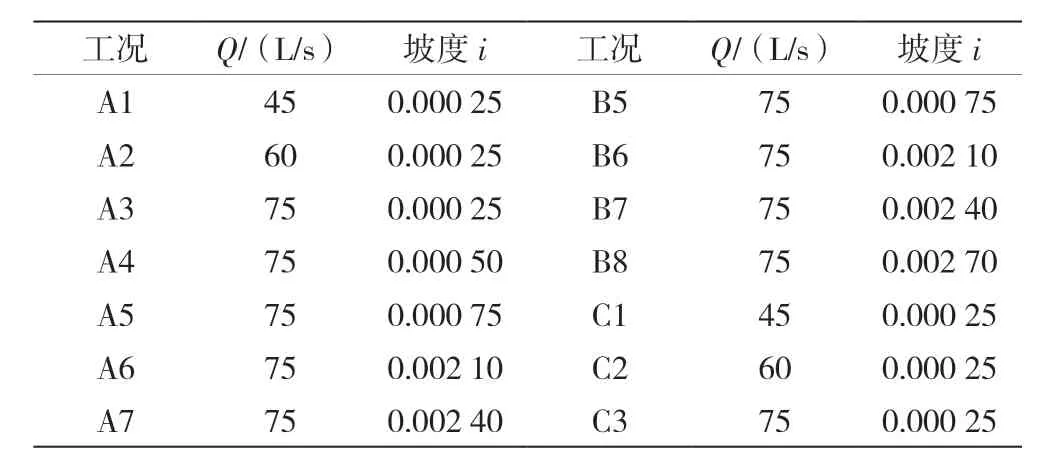
表1 试验工况参数

2 护岸糙率与综合糙率的关系

明渠恒定非均匀流曼v 宁糙率系v数 n,其基本公式如下：

对于均匀流,则可以简化成：

式中：n为糙v率；R为水力半径；A 为过流面积；zj为第j断面水深；j为第断面流速；U为断面平均流速；Lj为断面间距离；g为重力加速度；i 为底坡。

通常,由于不同材料和壁面形态,不同断面的糙率也不同,许多学者根据原型观测和试验研究,提出了计算综合糙率 nc的经验公式[7-8],其中应用较多的公式如下：

式中：nc为综合糙率；χ 为湿周；dj为第 j 个分割面的水深；nj为第 j 个分割面的糙率；χj为第 j 个分割面的湿周。

本文使用 PM 公式计算护岸糙率n ：

式中：nb为槽底糙率；nw为侧壁糙率；ns为护岸糙率；χb为槽底对应的湿周；χw为侧壁对应的湿周；χs为护岸对应的湿周。

本试验水槽底部与侧壁均为光滑玻璃材料,糙率n 取0.0095。

在不同护岸条件下,综合糙率 nc和水深 H 可使用回归分析建立相关关系式。得出对数关系式：

式中：a 与 b 是系数。

拟合结果见图2 和表2,其中 R 为数据拟合相关系数,3 种护岸的相关系数均大于0.9,说明整体拟合效果较好。3 种护岸综合糙率的变化情况相似,均随流量增大而增大,随底坡增加而减小。其中护岸A 糙率最小,护岸C 糙率最大,综合糙率随水深的增加而增大。以护岸 A 为例,nc值在底坡由0.00025 增加至0.0027 的过程中下降了16.4%,流量由45 L/s 增加到75 L/s 的过程中增加了9.7%。表面上看糙率的变化与流量和底坡有关,但本质上是因为水深的变化引起的河道综合糙率变化。

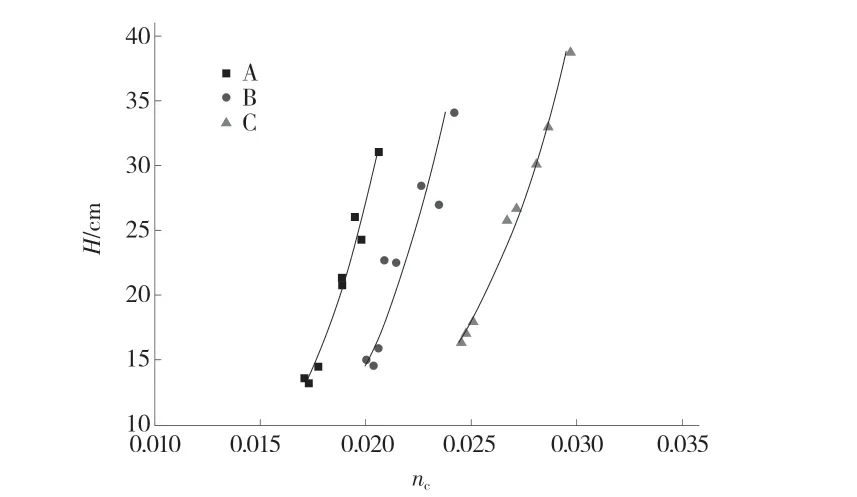
图2 综合糙率与水深的关系

表2 综合糙率与水深的拟合结果

图3 为综合糙率 nc和护岸糙率 ns随弗汝德数 Fr值的变化。可以看到在各种工况下均为缓流（Fr在0.109~0.598 之间）。

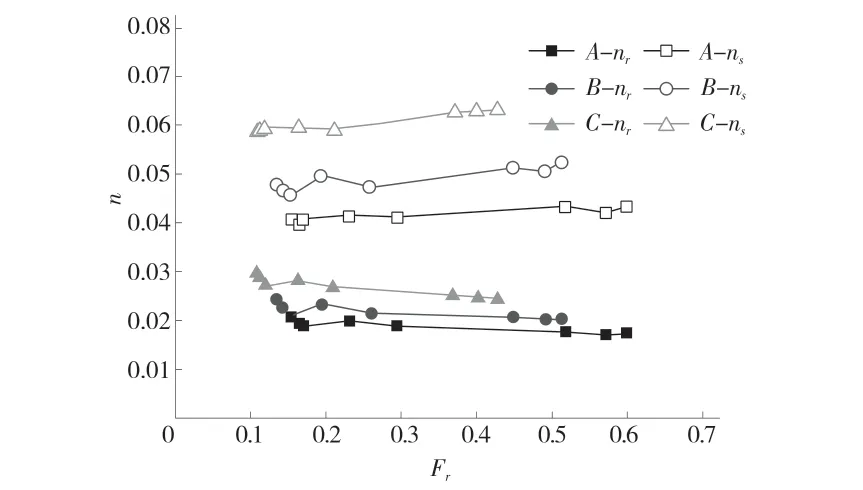
图3 糙率与弗汝德数的关系

随着弗汝德数的增大综合糙率下降,综合糙率的变化快慢与弗汝德数的取值有关,弗汝德数越小,糙率变化越快,弗汝德数越大,糙率变化越慢。不同护岸条件下的糙率最大值和最小值的差值均小于10%,表明流量和底坡的改变虽然对护岸糙率系数值有一定的影响,但影响程度较小,在此情况下护岸糙率可以取所有工况糙率的均值,护岸 A、B、C 的糙率分别为0.0415、0.0489 和0.0605。

3 护岸糙率对水面线的影响

为了弥补物理试验的不足,利用数值模拟的方法,采用HEC-RAS 模型对水面线进行计算,分析河床糙率变化对河道行洪能力的影响。

首先使用A1~A8 的数据对HEC-RAS 模型的准确性进行验证,结果表明模拟结果与实测结果的平均误差在1.26%左右,二者结果基本吻合。表明模型计算精度较高,可供进一步分析和计算。

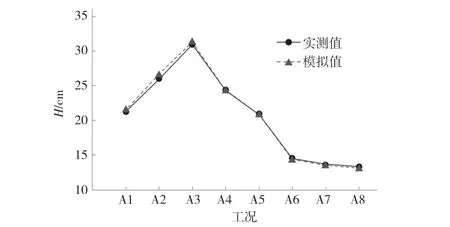
图4 A1~A8 工况模拟值与实测值对比

在HEC-RAS 模型中设置4 组不同的河道宽度B,来研究不同宽深比情况下护岸糙率与水面线的关系,为便于对比分析,每组底宽取临界水深下相应的流量。设计工况见表3,表中 hk是临界水深。

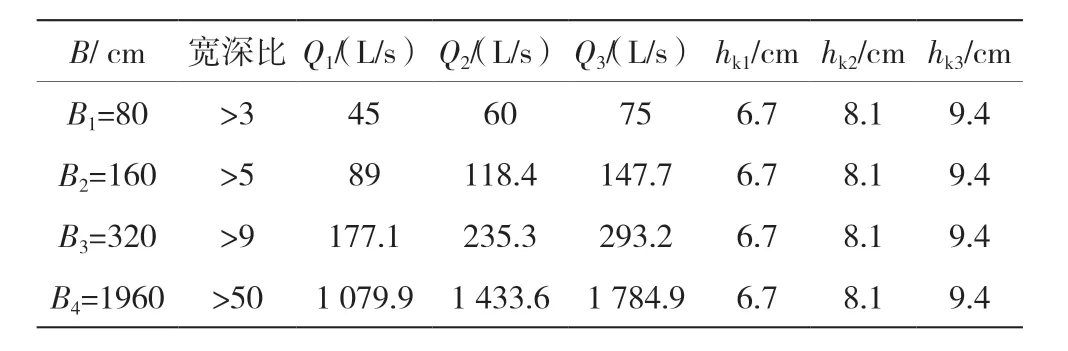
表3 设计工况

（1）当底宽和流量相同时,增加护岸糙率会增加河道的综合糙率,从而使正常水深增大。

（2）当底宽相同时,流量大小对水深和护岸糙率基本无影响。

（3）河道宽度增加,水深减小,从而使护岸湿周占总湿周的比重减小,河道综合糙率也随之减小。以Q1为例,当 B从80 cm 增加至320 cm 时,最大水深与最小水深之比由1.90下降至1.38；底宽1960 cm 时,当 ns从0.0208 增加至0.0726时,综合糙率的变化幅度仅为11%,相应水深仅增加6.6%,由此可得护岸糙率变化对水深影响不大。

图5 不同工况水深的变化

由以上结果可知,在河道较窄,宽深比较小的情况下,综合糙率受护岸糙率的影响较大；在河道较宽,水面线较浅时,综合糙率受护岸糙率影响较小,护岸糙率的改变对河道行洪能力几乎没有影响。

为进一步探讨护岸糙率对水位的影响,选取了45 L/s、0.002、边界条件10 cm、护岸糙率0.0415、ns变化幅度分别为-50%、-20%、0、+20%、+50%来模拟非均匀流。与均匀流工况相似,随着护岸糙率的增大,河床的综合糙率增加,河道沿程水深也随之增大,但沿程综合糙率值随水深的变化而不再保持恒定,而是随水深减小而减小。

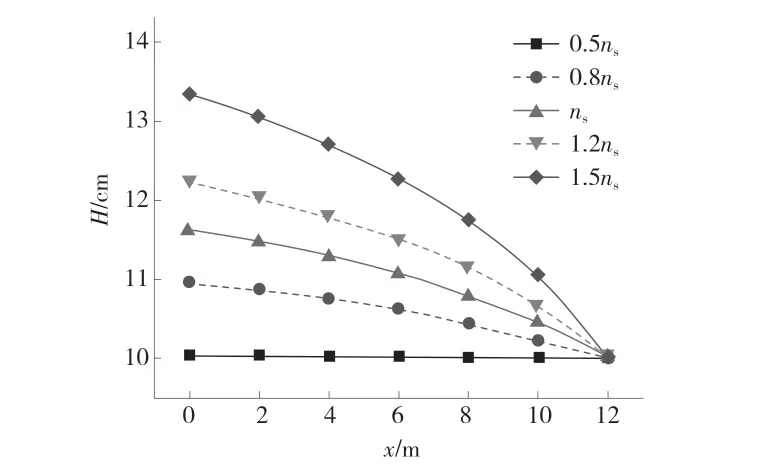
图6 水深在不同护岸糙率情况下随沿程的变化

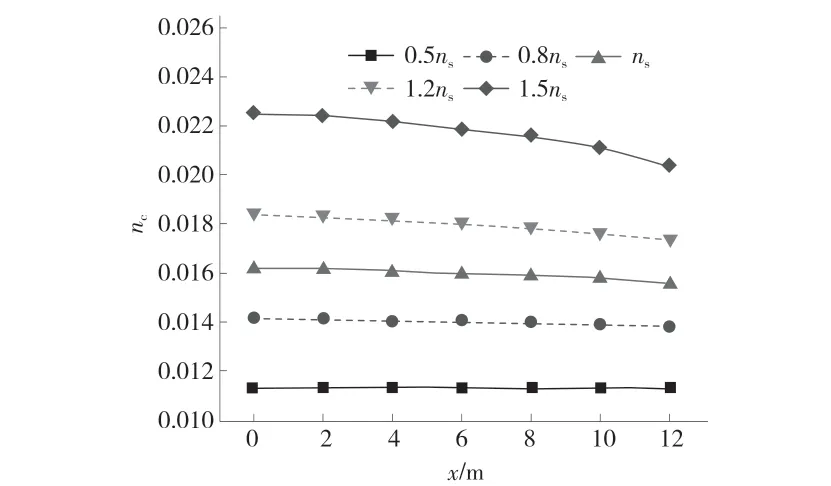
图7 综合糙率在不同护岸情况下随沿程的变化

4 结论

（1）本文通过室内试验和数值模拟,得出在均匀流条件下,河道综合糙率对护岸糙率的变化而变化,二者呈现明显的正相关性,糙率的变化进而引起水深的变化；当底宽不变时,不同流量情况下,水深随护岸糙率变化趋势基本相同。非均匀流条件下,护岸糙率越大,沿程水深越大；综合糙率沿程随水深减小而减小。

（2）3 种护岸糙率差异较大,同一护岸条件下,水深越深,护岸湿周占总湿周比重越大,河道综合糙率越大。

（3）对于宽度较小水深较深的河道,改变护岸糙率会明显改变水深；而宽度大水深浅的河道,护岸糙率对水深的影响较小,对河道行洪能力的影响也较小。