基于河道行洪能力的护岸糙率影响分析

孙礼珩

(庄河市水务事务服务中心，辽宁 大连 116400)

河道糙率是敏感而重要的河道水力计算参数，也是准确衡量河流阻力的关键系数。研究评价河道输水条件及行洪能力时，河槽糙率作为一项重要的指标，在很大程度上决定了河道的安全运行和防洪评价。

关于河流中植被的阻水特性国外诸多学者开展了深入研究，如漂浮、淹没和挺水等植被类型的研究。例如，Luhar等探究了曼宁糙率系数与河流中植被的分布形式、柔韧性等性质之间的关系；Aberle等探析了柔性和刚性非淹没植被在河道尺度至孔隙尺度上的阻力特性。此外，在人工渠槽糙率、糙率对过流能力的影响、天然河道糙率率定等方面国内学者也开展大量的研究。随着环境保护及生态治理的持续推进，生态护岸及含植被河道的等效糙率问题逐渐引起学者的关注，如孙东坡等[1]通过对连锁砖护面阻水特性的深入研究，揭示了水流速度与新型生态防洪结构糙率间的关系；张玮等[2]以草皮护坡为例，通过试验研究分析了河道糙率受生长期、土壤类型的影响，在此基础上提出了适宜的糙率取值区间；吴乔枫等[3]将河道断面按照植被分布特征进行分区，并在河道糙率计算公式中引入分区糙率系数；韩丽娟等[4]揭示了河道水流阻力与漂浮植被之间的相互关系；郑爽等[5]采用明渠水流下柔性植被淹没试验，提出基于经验的曼宁糙率系数等效计算公式在岸坡与主槽共同影响下的梯形河道水流，水流结构和河道阻力会因护岸类型的改变而改变，从而在一定程度上影响河道的行洪能力。因此，必须全面探究河道的行洪能力受护岸糙率特性的影响。文章综合利用数值模拟与室内试验的方法，研究了不同护岸类型下梯形断面河道的糙率变化规律，在此基础上探析河道行洪能力受护岸糙率变化的影响，以期为防汛调度研究、生态护岸防洪评价等提供理论支持。

1 试验概况

本研究利用深0.8m、宽1.5m、长20m的矩形变坡循环水槽开展试验，为保证入流平稳将稳流装置设于水槽进口段，水深的控制利用出口段栅栏式尾门实现，并采用电磁流量计和阀门计量、控制流量。试验段选取为水槽居中12m范围，梯形非对称断面利用有机玻璃板布置，河道斜边坡宽0.4m、主槽宽0.8m。采用护坡结构与草本植物构造新型生态护岸类型，并将8mm厚的仿真草皮敷设于梯形边坡上，为了模拟护岸上的挑流消能结构在草皮上黏贴有机玻璃材质的直三棱柱砖块。试验所用的砖块尺寸有3种，并命名底面与砖块迎水面夹角15°、30°、45°的护岸为A护岸、B护岸、C护岸，布设砖块的横向与横向间距0.05m、0.4m。

水位测量断面每隔2m沿试验段均匀布置，稳定均匀流利用尾门开度的调节控制来实现，并以各断面水深差不超过1mm作为均匀水流的判断标准。通过设置不同的坡底和流量工况，对3种护岸开展均匀流试验，从而获取各条件下的均匀流水深，试验工况，见表1。其中，A、B、C护岸的试验分组为A1-A8、B1-B8、C1-C8，i、Q为底坡和流量参数。

表1 试验工况

2 护岸糙率

采用计算公式(1)求解恒定非均匀流明渠曼宁糙率系数n，即：

(1)

式中：A、R、Q为断面面积、水力半径和流量；zj、vj为断面j的水深和流速；Lj为上、下游断面间的距离；n、g为糙率系数和重力加速度。均匀流条件下，糙率系数n可利用简化公式求解，即：

(2)

式中：i、U底坡和断面平均流速。

一般地，由于壁面形态或组成材料的差异河道过水断面各部分糙率不尽相同，基于试验研究或原型观测许多学者提出了相应的经验公式，较为常用的综合糙率nc计算方法有PM公式、EBM公式、KCM公式，具体如下：

(3)

(4)

(5)

式中：nc、nj为综合糙率和分割面j的糙率；x、xj为总湿周和分割面j的湿周，其中x=xb+xw+xs；dj为分割面j的水深。本研究考虑利用PM公式求解护岸糙率ns，其表达式为：

(6)

式中：nc为综合糙率；ns、nw、nb为依次代表护岸、侧壁和槽底的糙率系数；xb、xw、xs为依次代表护岸、侧壁和主槽的湿周；x为总湿周，x=xb+xw+xs。

水深与综合糙率的关系，见图1。水深与综合糙率之间的相关关系利用回归分析法构造，其表达式为：

nc=aInH+b

(7)

式中：a、b为系数值。

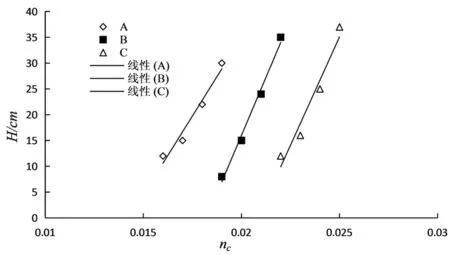
图1 水深与综合糙率的关系

引入拟合相关系数R，水深与综合糙率拟合值，见表2，从表2可知各护岸的R值均超过0.9，可见数据拟合具有较好的效果。此外，随着水深的增加综合糙率呈现出不断增大的变化趋势，这与边坡阻力较大而河床阻力较小的糙率分布规律保持较好一致性；不同护岸的综合糙率存在一定差异，其中糙率值最小的为护岸A，而糙率最大的为护岸C。护岸相同的条件下，随着流量的增加综合糙率值不断增大，随着底坡的增加综合糙率不断减小。以护岸A为例简要说明其变化特征，从45L/s不断增大流量至75L/s，该过程中nc值增加了9.5%，从0.00025不断增大底坡至0.0028，该过程中nc值增加了16.8%。通过分析糙率受底坡、流量的影响发现，河道综合糙率的变化实质上是与水深的改变有关。

表2 水深与综合糙率拟合值

随弗劳德数Fr的变化护岸糙率ns及综合糙率nc的变化，弗劳德数Fr与糙率间的关系，见图2。弗劳德数Fr在各工况条件下的取值区间为0.108-0.596，试验中始终保持缓流状态。研究表明，随弗劳德数Fr的增加综合糙率不断减小，弗劳德数Fr较小时综合糙率具有较快的变化速率，而弗劳德数Fr较大时综合糙率具有较慢的变化速率，该研究成果与矩形渠道研究规律保持一致。最小值与最大值糙率之差，在不同护岸条件下不超过10%，可见护岸糙率系数值受底坡或流量改变的影响较低，护岸糙率值可以取各工况情况下糙率的平均值。因此，护岸A、护岸B、护岸C的糙率值ns依次为0.0418、0.0470、0.0637。

图2 弗劳德数Fr与糙率间的关系

3 河道行洪能力影响

近年来，随着计算机的快速发展，数值模拟技术被越来越多的用于河道水动力计算研究，从而有效解决物理模型及原型观测试验存在的问题。文章拟对河道一维水流水面线利用河流动力学模型HEC-RAS计算，在此基础上揭示河道行洪能力受护岸糙率变化的影响特征[6-8]。

首先，通过模拟计算A1-A8工况检验HEC-RAS模型的精准度，设置右岸侧壁与河底糙率0.0092、左岸护岸糙率0.0418，建立梯形河道模型确定各工况下的水面线，并对比分析模拟值与试验数据，A1-A8工况下试验与模拟结果，见图3。从图3可知，实测值与模拟值具有较高的吻合度，3种工况下的平均误差都≤1.20%，可见该模型具有较高的计算精度，能够用于河道行洪能力的计算分析。

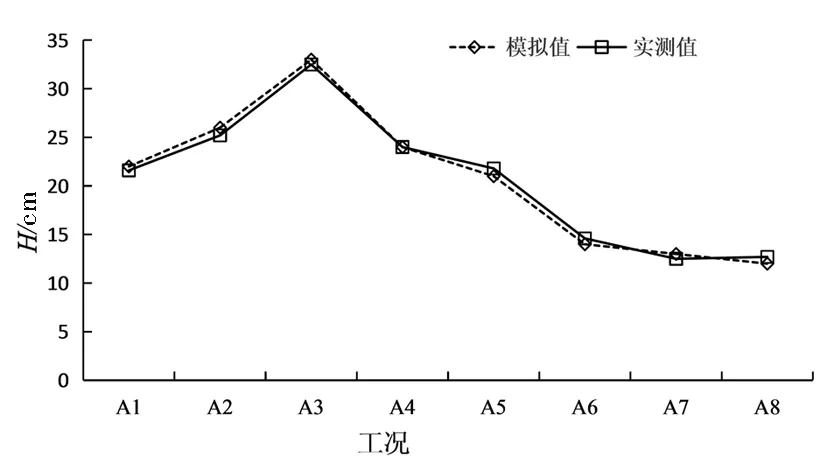
图3 A1-A8工况下试验与模拟结果

为进一步探究水面线受不同宽深比条件下护岸糙率变化的影响，通过改变河底宽度B设置4组不同底宽工况，以3种不同流量条件依次开展每组底宽工况的试验研究。保持临界水深hk不变，在不同底宽条件下选取所对应的流量值，以更加直观的对比分析，工况设计，见表3。

表3 工况设计

各工况下的水深变化规律，见图4。由此可以得出以下结论：①保持流量与底宽相同的条件下，河道综合糙率随着护岸糙率的增加而增大，从而使得正常水深有所增加；②保持底宽不变的条件下，护岸糙率ns与水深H的变化趋势受流量改变的影响较小；③随底宽的增大河底宽深比、河道水深不断增加，河道综合糙率系数和护岸部分的湿周权重比不断减小。以Q1为例简要说明其变化特征，从70cm不断增加河底宽度B值280cm条件下，不同护岸糙率ns所对应的最大与最小水深比从1.80不断减小至1.26；护岸糙率ns在底宽1680cm工况下从0.0206增大至0.0725，从0.094综合糙率逐渐增大至0.0106，该过程中水深增加6.5%，可见河道水深受改变护岸糙率的影响较小。

图4 各工况下水深变化规律

研究表明，对于窄深型河道(即宽深比较小的河道)，河道水深受改变护岸糙率的影响较大，即护岸糙率与综合糙率的比值较高；对于宽浅型河道(即宽深比较小的河道)，护岸糙率与综合糙率的比值较小，河道水面线受不同护岸糙率的影响较弱，即河道行洪能力受改变护岸糙率的影响较低。

鉴于水位与护岸糙率在非均质流条件下的关系，设置底坡0.005、流量45L/s、护岸糙率ns0.0410、下游水深边界条件10cm，率ns变幅设为+50%、-%、+20%、-20%、0，由此揭示综合糙率率nc及水深H在不同工况下的沿程变化规律，不同护岸糙率下的沿程变化，见图5。结果发现，综合糙率、河道沿程水深随护岸糙率的增加均不断增加，该变化规律与均匀流保持一致。相对于均匀流工况，非均质流沿程的综合糙率由于水深的沿程变化不再恒定，随水深的降低沿程综合糙率呈不断减小的变化特征，该变化规律与试验研究相吻合。

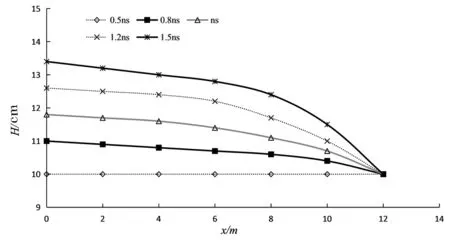
(a)水深变化

(b)综合糙率变化

4 结 论

文章结合数值模拟和室内试验法，探究了河道行洪能力受梯形河道护岸糙率变化的影响，主要结论如下：

1)不同护岸工况的糙率值存在差异，保持护岸不变的条件下，随水深的增加河道综合糙率不断增加，并且呈现出对数变化规律，而护岸糙率值受底坡或流量改变的影响较小。

2)均匀流工况下，河道综合糙率随护岸糙率的增加而增大，从而增大了正常水深；保持底宽不变的条件下，随护岸糙率的改变改变流量对水深变化趋势的影响较小；非均匀流工况下，随护岸糙率的增加河道沿程水深不断增加；随水深的降低沿程综合糙率呈现出减少的趋势。

3)对于窄深型河道，河道水深受改变护岸糙率的影响较大；对于宽浅型河道，护岸糙率与综合糙率的比值较小，即河道行洪能力受改变护岸糙率的影响较低。