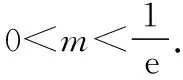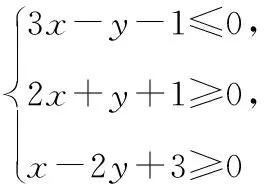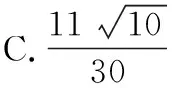都是图形“惹的祸”

内蒙古 姬恩泽

数学语言分为文字语言、符号语言和图形语言,它们在阐述数学问题时互相补充、互相印证.图形作为一种数学语言,以其直观性与形象性,支起了数学的半壁江山,华罗庚先生说“数无形时少直觉”.图形语言是以结构联系为对象的关系语言形式,是一种视觉语言,它为数学对象、性质提供直观的对应关系模型,有利于形成直接印象和直觉思维.“枯燥而无趣”的数学问题在“图形”的帮助下,才有了“生命力”.

可见,图形在数学解题中起到很重要的作用,有些数学问题在没有图形辅助的情况下,解题思维几乎无法开展.正是因为数学知识的呈现离不开图形,所以图形是解决数学问题的“突破口”.但是,通常我们在解题时都是徒手作图,也就是我们画出的是“草图”,如果这么重要的图形一旦出现了偏差,解题结果注定是错误的.可见,图形的精准性实在不容小觑.下面结合具体问题列举并简析常见的图形偏差,诚望引起大家的切实重视.

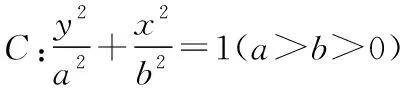
(1)求椭圆的方程；

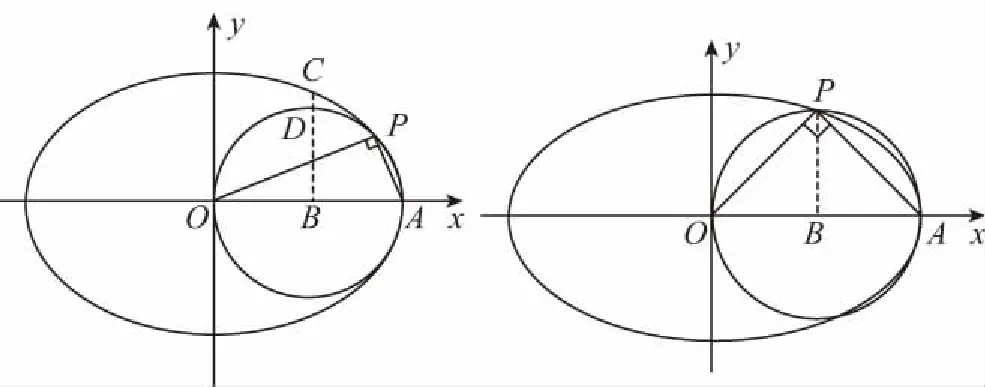
(2)已知过T(0,2)的直线l与椭圆C交于A,B两点,若在x轴上存在一点E,使∠AEB=90°,求直线l的斜率k的取值范围.

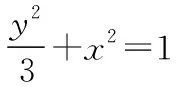
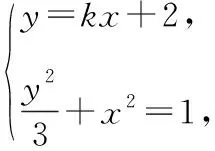
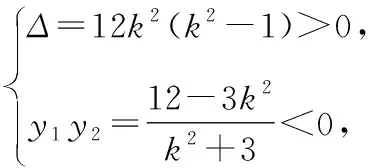
解得k<-2或k>2,故直线l的斜率k的取值范围是k<-2或k>2.

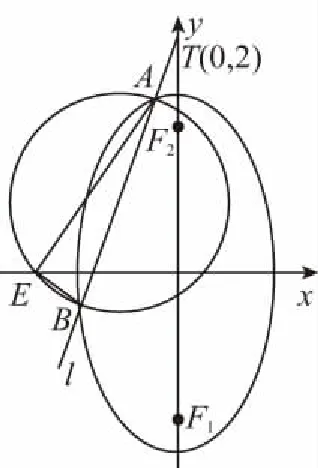
【错误分析】这个解题思路似乎“合情合理,顺理成章”,但是结果是错误的！那么究竟错在哪里了呢？再回头看看本题中的图形,仔细推敲,可以发现图中有一个严重的漏洞,因为点A,B都是动点,即线段AB的长度不固定,从而作出的圆大小不定,故该圆的直径两个端点A,B两点分别位于x轴的上侧和下侧是错误的,那么A,B这两个点的纵坐标也就不一定异号,如图所示,即y1y2<0是不对的,故y1y2<0是导致结论错误的“罪魁祸首”.

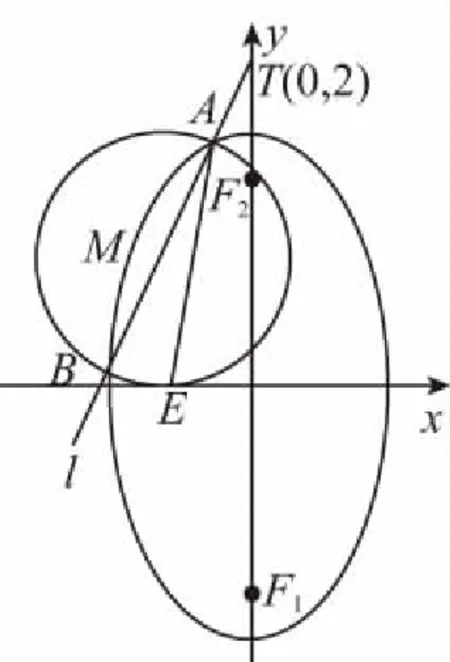
(2)【正解】设A(x1,y1),B(x2,y2),AB中点M(x0,y0),

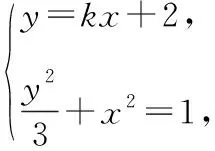
消去y,得(k2+3)x2+4kx+1=0,

且Δ=12k2-12≥0,

所以k≤-1或k≥1,……①

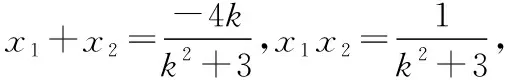
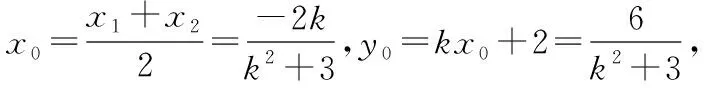
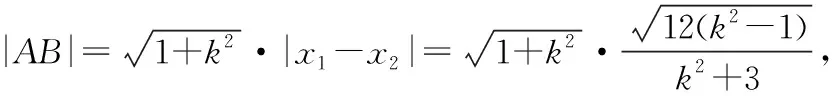
若在x轴上存在一点E,使∠AEB=90°,

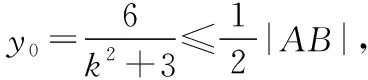
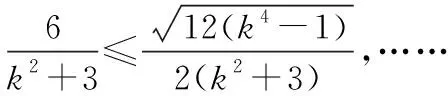
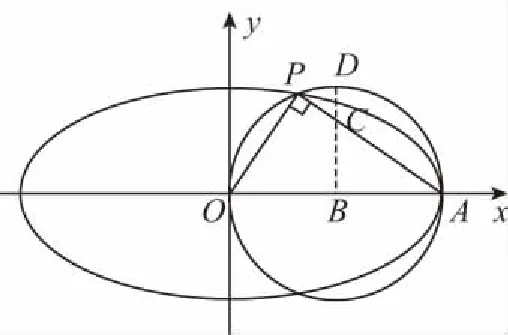
【例2】设椭圆上存在一点P,它与椭圆中心O的连线和它与长轴一个端点的连线互相垂直,则椭圆离心率的取值范围是________.

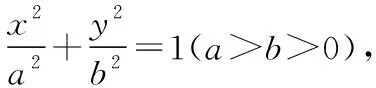
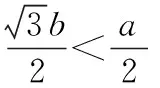
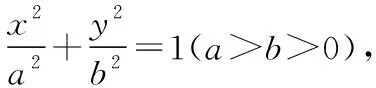
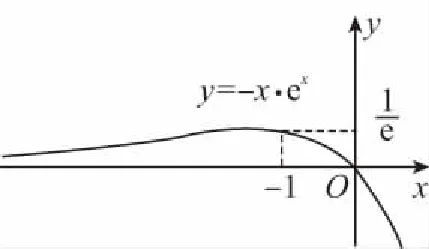
【例3】若函数f(x)=x·ex+m有且只有两个零点,求实数m的取值范围________.

【错解】令f(x)=x·ex+m=0,

则m=-x·ex,令g(x)=-x·ex,

则g′(x)=-ex-x·ex=-ex(x+1),

令g′(x)=0,得x=-1,

当x<-1时,g′(x)>0,

故函数g(x)在(-∞,-1)上是增函数；

当x>-1时,g′(x)<0,

故g(x)在(-1,+∞)上是减函数；

故函数f(x)图象大致如图所示,

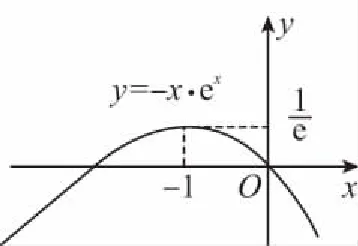
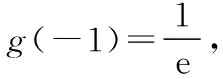
而函数f(x)=x·ex+m有且只有两个零点,

【错误分析】这个解题思路也似乎“顺理成章”,但是结果却是错误的！那么究竟错在哪里了呢？回顾解题思路,由函数g(x)在(-∞,-1)上是增函数,在(-1,+∞)上是减函数,我们“随心所欲”作出的函数图象“出问题”了,因为通常情况下,一个函数在x=-1两侧的单调性相反,很自然的就画出类似抛物线的形状,但是,这里面含了一个特殊函数y=ex,它的值域恒正的特性被忽视,从而导致了图象出错.

【正解】令f(x)=x·ex+m=0,

则m=-x·ex,令g(x)=-x·ex,

则g′(x)=-ex-x·ex=-ex(x+1),

令g′(x)=0,得x=-1,当x<-1时,g′(x)>0,

故函数g(x)在(-∞,-1)上是增函数；

当x>-1时,g′(x)<0,

故g(x)在(-1,+∞)上是减函数；

所以当x=-1时函数g(x)有最大值,

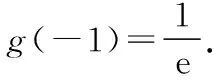
另外,由于当x<0时0

则g(x)=-x·ex>0；

当x>0时ex>1,则g(x)=-x·ex<0；

且当x=0时g(0)=0,则函数g(x)的图象如图所示,

( )

【错误分析】这个解题思路貌似正确,而且备选四个答案中也有这个结果,但是答案是不正确的,那么问题出在哪里了呢？回顾解题的过程非常合情合理,唯一可能出现错误的只有我们画出的“草图”,因为是徒手作图,所以不免有“误差”,可能导致图形“失真”,从而点、线的位置关系不准确,才导致错误.通过电脑精确作图,发现这里点D的位置是不正确的,过点D向可行域的边界AB作垂线段,发现垂足并不落在边界AB上！也就是说我们求出来的最优解并不在可行域内,从而导致结论错误.

总之,准确的数学图形在解题过程中起到了举足轻重的作用,它能迅速明确题目中的各个元素、变量之间的关系,清晰地提取出关键条件,甚至是题目中的隐含条件,也只有恰当的利用了这些几何图形及其特点,才能建立几何概念,理解几何关系,并应用这些概念和关系建立起数学模型,迅速找到解题思路.