把握本质 感受价值
程佳杰
【摘 要】数与形是数学研究对象中两个十分重要的方面,“数形结合”不仅是一种解题方法,而且是一种重要的数学思想。在教学中要了解数形结合思想产生与发展的背景,把握数形结合思想的本质,设计合理的教学环节,使学生充分感受数形结合的价值,形成良好的数学意识。
【关键词】数形结合;数学史;思想价值
数形结合思想就是通过数和形之间的对应关系和相互转化来解决问题的思想方法。这里的数与形既对立又统一,在一定条件下是可以转化的。
北京教育学院刘加霞老师认为,借助于直观形象模型理解抽象的数学概念以及抽象的数量关系是小学生学习数学的重要方法,但这一方法与数学意义上的“数形结合”方法的内涵不一致,它至多只能是“数形结合”方法的雏形。在教学中,要充分了解数学思想产生与发展的背景,把握这种思想的本质。只有这样,才能设计出合理的教学环节,使学生充分感受数学思想的价值,形成良好的数学意识。本文就结合人教版六年级上册“数与形”例1的教学,谈一谈这方面的体会。
一、打通“式”“数”和“形”之间的联系,找到隐藏的规律

“数与形”例1的素材原型是古希腊的拟形数。毕达哥拉斯学派在研究数时,常常和平面上的点联系起来,按照点的形状将数进行分类,同时结合图形的性质来研究数的性质,这是一次成功的尝试,由于“形”的介入,有力地推动了“数”的发展。古希腊的拟形数有很多,常见的有三角形数、正方形数、五边形数等(如图1)。
例1研究的是正方形数,深入分析后不难发现,这里要打通的是“代数式”“数”与“形”之间的关系,因为“数形结合”中的“数”有时是一个数,也可以是数量关系,还可以是一个代数式,进入第三学段后,数形结合中的“数”更多的是以方程和函数式的形式出现。在例1 的素材中,代数式与正方形是一种对应统一的关系,代数式中的每一项都能在正方形中找到对应的那个“零件”,而这个式子加起来的和又与“形”中小正方形的总数相对应。厘清了这些基本要素后,要考虑的是以怎样的路径切入,是由“数”到“形”呢,还是由“形”到“数”呢?经过思考,我认为由“形”到“数”更加合理,一是符合拟形数的产生背景,二是有利于学生自主探究活动的实施。具体教学环节如下。
1.为学生提供大小一样,4种颜色(红色1个,绿色3个,黄色5个,蓝色7个)共16个小正方形。并提出活动要求:分一分、摆一摆,根据摆法写出对应的算式。
2. 学生完成后,教师组织反馈活动。学生借助摆成的边长为4的正方形,得到了“1+3+5+7”和“4×4”之间的相等关系。把“4×4”改写成“42”后,得到等式:1+3+5+7=42。
3.根據算式“1+3+5+7=42”和拼成的正方形,引导学生思考:你还想到了哪些问题?学生很自然地想到:如果把这个边长为4的正方形再变大一些能得到怎样的算式呢?或者再变小一些能得到怎样的算式呢?在问题引领下,学生进一步开展探究活动,得到了下面的等式:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
1+3+5+7+9+11=62
……
4.引导学生找到规律,并准确表述。
通过观察、操作和思考,引导学生利用若干个数、式、形中存在的有限的规律,推理得到一般性结论,并进行准确的表述。
二、逐步提升问题的难度,感受以形助数的价值
在学生找到了“数”与“形”之间的规律后,就需要让他们在实践运用中体会“以形助数”的优势。这个环节安排了这样三道习题。
第1题:1+3+5+7+9+11+13+15=( )2
第2题:1+3+5+7+……+( )=202
第3题:1+3+5+7+……+2017=( )2
这三道习题在难度上呈现层层递进的态势。第1题的难度比较低,意图是让学生运用第一环节的研究成果,初步感受数形结合的价值。第2题在第1题的基础上增大了数据,其目的是引导学生结合图形,发现拼成后的大正方形边长与最外层“┓”数量之间的关系。在正方形数中,最外层“┓”数量是一个很关键的数据,因为它决定了拼成的正方形的边长,换言之,最外层“┓”数量决定了正方形的量化特征。通过查阅相关资料,我们了解到古希腊人也是循着这条路径去研究的,他们把这个形状称作“磬折形”,毕达哥拉斯学派很重视这方面的研究。因为找到了最外层“┓”数量与正方形边长之间的关系就等于找到了一条连接“数”与“形”的快速通道。在寻找这条“通道”的过程中,加深了学生对数形结合思想价值的理解。第3题在第2题的基础上,继续提升难度,增加数列的项数,同时改变了思考方向,其目的还是引导学生借助对图形的想象与思考,使其对最外层“┓”数量与正方形边长之间的关系更加清晰,使学生对数形结合价值的体会更加深刻。
三、引导学生研究新的问题,深化对数形结合思想的认识
从数学文化的角度来讲,数学文化最核心的内容是数学的思想、精神和研究方法,那么,怎样才能接近这些核心的部分呢?一条有效的途径就是让学生提出有价值的问题并解决这个问题,在思考和实践的过程中感受数学的思想和方法。基于这样的思考,在学生通过探究活动沟通了等差数列1,3,5,7……的和与正方形之间的关系后,引导学生思考:由此你还想到了什么问题?果然是一石激起千层浪,学生提出了很多新的问题,既然有正方形数,是不是还有三角形数、长方形数、梯形数等其他多边形数呢?还有的学生则从数列的角度提出了:刚才研究了从1开始的连续奇数相加与正方形有关,那么从2开始的连续偶数相加可以摆成什么图形呢?从1开始的连续自然数相加又可以摆成什么图形呢?虽然这些问题是从两个角度提出的,但有一点是一致的,那就是都在原有活动经验的基础上,试图去寻找更多的关于“数”与“形”之间的联系,结合“形”的特征来得到更多“数”的性质。这种想法与古希腊拟形数的产生背景和发展历程是一致的,充分体现了数学文化的核心价值,是非常可贵的。
在学生提出了多个问题后,让学生选择其中一个共同研究,大多数学生选择了“从2开始的连续偶数的和可以摆成什么形状”这个问题。于是把这个问题拿出来共同研究,为了激发学生的挑战欲,把算式的末项定为2018,就得到了这样的式题:2+4+6+8+……+2018=( )。学生在研究新问题的过程中,果然迁移了上面的研究方法,也采用了摆一摆、画一画的方法。从第1项“2”开始,再到“2+4”,“2+4+6” ,“2+4+6+8”……学生依次画出了这样的图形(如图2),也有学生把小方块简化为一个圆点,画出了这样的图形(如图3)。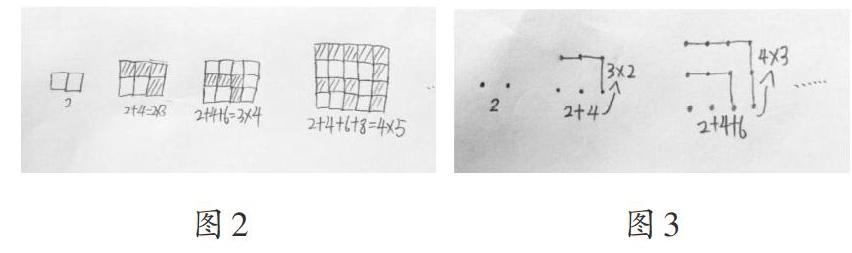
在此基础上,学生开始关注最外层“┓”数量与长方形的长、宽之间的关系,有的学生发现最外层“┓”数量再加上1的话,就把右上角重叠的那一个补上了,就得到了长与宽的和,因为拼成后的长方形长总是比宽多1,把得到的和拆成两个连续自然数,就得到了长和宽。如图2最右边的长方形中,最外层“┓”数量是8,加上1后得到9,把9拆成相邻的两个自然数得到4和5,4就是长方形的宽,5就是长方形的长,于是得到总数为4×5=20。还有的学生发现把最外层“┓”数量除以2就是宽,宽加上1就得到了长。不管是哪一种方法,说明学生都关注到了这个数列中的最大数,因为这个数决定了拼成后的长方形的量化特征。把这个规律一般化后,学生借助对图形的想象和分析,很快找到了“2+4+6+8+……+2018=( )”的解决办法。在上述过程中,有方法的迁移,也有思维的碰撞,更多的是对数形结合思想的感悟与运用。
数学的学术形态通常是冰冷的,但是若能了解其发生和发展的过程,就能更好地把握其本质,设计出合理的教学环节,引发学生火热的思考,让学生在思考与实践中感受数学的价值与魅力。
参考文献:
[1]刘加霞.“数形结合”思想及其在小学数学教学中的渗透(上)[J].小学教学(数学版),2008(4).
[2]Mario Livio.数学沉思录——古今数学思想的发展与演变[M].黄征,译.北京:人民邮电出版社,2010.
(杭州师范大学附属乍浦实验学校 314201)

