一种新的评价结构方程模型拟合效果的校正拟合指数*

王　凯　陈方尧　谭　铭　陈平雁△

【提　要】　目的　建立一种新的用于评价结构方程模型(SEM)拟合效果的方法—校正拟合指数(CGFI)。方法　在已有拟合指数(GFI)方法的基础上，通过增加1/(N-1)项校正样本量导致的低估效应，通过自由度与变量个数的比值项对模型的复杂程度进行惩罚，构建了CGFI，表达为:CGFI=1-[dftest/k(k+1)][1-GFI-1/(N-1)]。基于预设的SEM，采用Monte Carlo技术模拟产生数据，考虑样本量、参数估计方法、模型误设类型及误设程度四种因素，将所提出的CGFI与其他3种拟合指数(GFI，AGFI，PGFI)进行比较。评价标准基于稳健性和对模型误设的敏感性。结果　CGFI较GFI有一定改善效果，受样本量的影响更小，对模型误设更为敏感；GFI和AGFI受样本量的影响较大，在样本量较小时存在一定低估。PGFI对模型误设不敏感，且存在较为严重低估。GLS参数估计方法在模型严重误设时容易得到反常的结果。结论　CGFI较GFI有较好的表现，临界值为0.95，可用于模型拟合效果的评价。

结构方程模型(structural equation modeling，SEM)拟合效果的评价有大量研究[1-5]。一般认为，一个良好的评价指数应该具备以下特性：①对各类型模型误设(指模型参数的错误设定，如当总体参数非零时将其设定为零等)敏感；②不受样本量、数据分布形态和参数估计方法的影响；③对参数过多的模型进行惩罚[6-7]。

Joreskog和Sorbom[8]提出了拟合指数(goodness-of-fit index，GFI)方法，其思想是度量样本协方差阵和理论模型协方差阵之间接近的程度；GFI值越大拟合效果越好。GFI虽然是最常用的指标，但对其却褒贬不一。Bollen和Stine[9]发现，当模型严重误设时会出现GFI值较大的矛盾结论；Gerbing[10]和Marsh[11]指出，GFI和样本量之间存在较大的正向相关关系，并在样本量有限时存在一定的低估。而Tanaka[12]和Sugawara[13]认为GFI不受样本量和参数估计方法的影响。针对GFI可能存在的问题，Joreskog[8]和Mulaik[14]先后提出对自由度和待估参数进行惩罚的调整GFI(adjusted-goodness-of-fit index，AGFI)和无偏GFI(parsimony unbiased goodness-of-fit index，PGFI)，理论认为这两种指数较GFI有更好的性能，但尚缺乏研究证据的支持。

鉴于GFI一类指数的不足，本研究将在GFI方法的基础上提出一种新的校正GFI(corrected goodness-of-fit index，CGFI)方法，以期较目前的GFI一类指数有更好的统计性能。

方　　法

1．GFI一类指数简介

GFI一类指数包括GFI,AGFI和PGFI，其定义和特性见表1。

表1　三种拟合指数的定义和特性

*：S-样本的协方差阵，Σ-估计的理论模型协方差阵，I-单位矩阵，dftest-理论模型的自由度，P-观测变量的个数。

2．校正GFI的提出

(1)

3．模拟研究的模型设定及参数选择

采用Monte Carlo技术，对研究提出的CGFI方法与其他GFI一类方法进行模拟比较。构建的理论模型见图1，包含4个潜变量，每个潜变量包括5个观测变量。

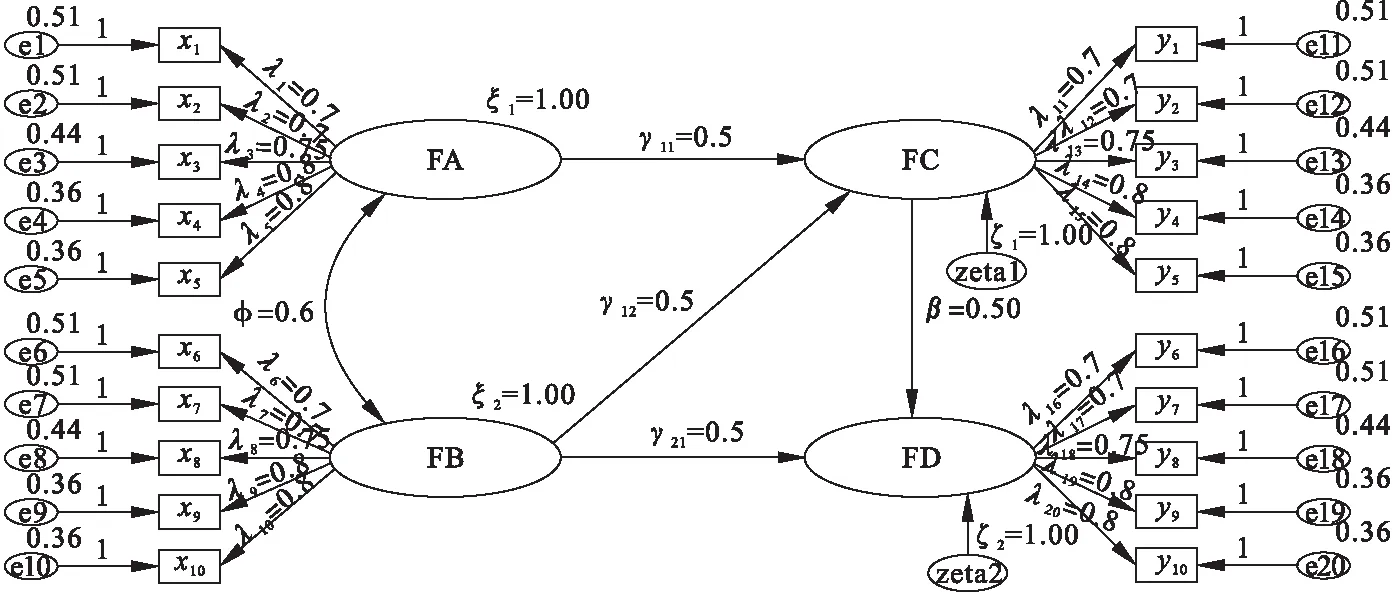
图1　理论模型图

本研究考虑两种模型误设类型：测量模型误设和结构模型误设(见表2)。

①测量模型的轻度误设为，将观测变量X5误设为潜变量FB的条目；重度误设为，将观测变量X5误设为潜变量FB的条目，观测变量X7误设为潜变量FA的条目。

②结构模型的轻度误设为，将FA和FB之间的协方差误设为0，FA和FC之间的回归系数误设为0；重度误设为，将FA和FB之间的协方差和所有的回归系数误设为0。

表2　模型设定情况

样本量设定为150,200,300,400,500,600,800,1000,1500,2000,5000共11种；参数估计方法为最大似然估计(ML)和广义最小二乘(GLS)2种。观测值服从正态分布。模拟次数设定为1000次。

4．数据及统计分析

模拟研究通过SAS(v.9.4;SAS Institute Inc,Cary,NC)实现。模拟数据通过SAS PROC IML产生，结构方程建模由SAS MACRO和SAS PROC CALIS完成[16]，所得结果进行基本描述分析和析因设计的方差分析，统计检验水准α为0.05(双侧)。

结　　果

1．负方差和迭代不收敛的情况

模拟研究中，迭代次数设置为1,000,000次，以避免迭代不收敛。本研究的后续分析是基于全数据集下的结果。负方差的情况见表3。结果显示，负方差的情况只在GLS方法下出现，测量模型误设更容易导致负方差的结果；同时模型误设程度越大，出现负方差的比例也越大。

表3　负方差的基本情况(GLS方法)

*：N var-负方差，P var-正方差，ML方法下没有出现负方差的情况，因此不在表中给出。

2．拟合指数的方差贡献率

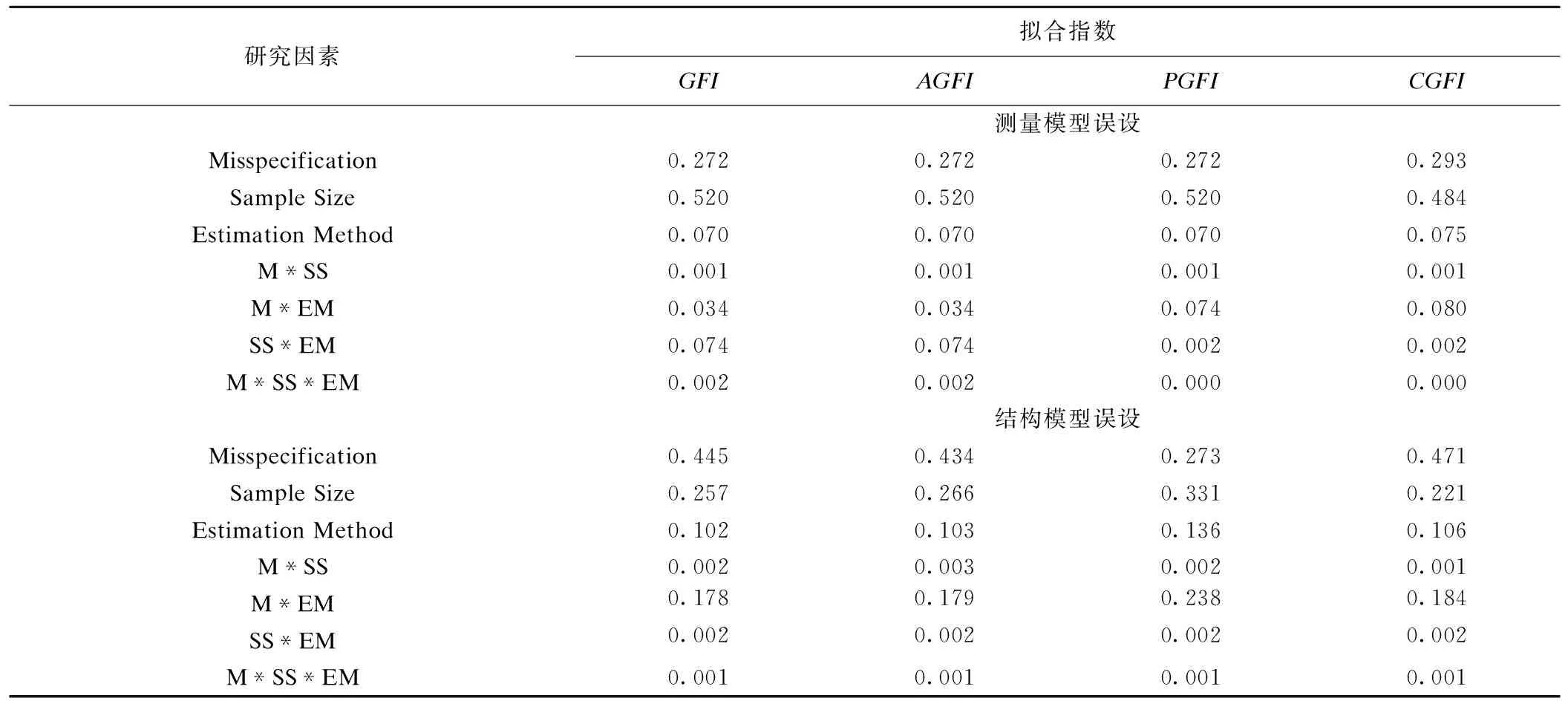
对模拟数据进行析因设计的方差分析，考虑的因素为样本量、参数估计方法、模型误设类型及误设程度，通过分析每个因素的方差占总方差的比例，即方差贡献率[2,16-19]，来量化评价各因素对拟合指数的影响大小。两种模型误设类型下各因素对拟合指数的方差贡献率结果见表4。

(2)

*：Misspecification(M)-模型误设程度，Sample Size(SS)-样本量，Estimation Method(EM)-参数估计方法。

如表4所示，测量模型误设下，GFI、AGFI、PGFI三种指数有一致的结果，受样本量的影响为0.520，对模型误设的敏感性为0.272；CGFI与其他三种指数比较，受样本量的影响有一定的降低(0.484)，对模型误设的敏感性也有部分提高(0.293)。结构模型误设下，不管是从样本量(0.221 vs 0.257)还是模型误设敏感性(0.471 vs 0.445)角度，CGFI都较GFI有一定的改善；AGFI和GFI有相似的结果，而PGFI较GFI来说，受样本量的影响更大(0.331 vs 0.257)，对模型误设较不敏感(0.273 vs 0.445)，表现出较差的效果。

3．不同模型下拟合指数随样本量的变化趋势

(1)真模型下拟合指数的变化趋势

图2显示，在真模型情况下四种指数分别采用ML和GLS方法时随样本量变化的趋势。采用ML方法，GFI和AGFI在样本量小于300时存在明显低估，并较大程度上受样本量的影响；当样本量逐渐增大时，这一现象逐渐消失，并趋近于理论真值。PGFI在所有样本量情况下都存在较严重的低估。相对而言，CGFI在样本量小于300时仅存在轻微低估，受样本量的影响也较小，说明CGFI优于GFI。

采用GLS方法的结果基本与ML方法一致。对比两种参数估计方法下的结果来看，真模型下四种拟合指数基本不受参数估计方法的影响，表现出较为稳健的结果。

图2　真模型下四种拟合指数在不同参数估计方法下随样本量变化的趋势

(2)测量模型误设下拟合指数的变化趋势

图3显示，在测量模型轻度误设情况下四种指数分别采用ML和GLS方法时随样本量变化的趋势。采用ML方法时，GFI和AGFI受样本量的影响较为明显，且在样本量小于300时存在一定低估，PGFI则存在明显低估。相比而言，CGFI受样本量的影响较小，在样本量小于300时有轻微低估。GLS方法的结果也基本一致。综合两种参数估计方法的结果看，CGFI的临界值应高于常规临界值0.90，初步确定为0.95。

图3　测量模型轻度误设下四种拟合指数在不同参数估计方法下随样本量变化的趋势

图4显示，测量模型重度误设情况下四种指数分别采用ML和GLS方法时随样本量变化的趋势。采用ML方法，结论基本和测量模型轻度误设下一致，CGFI基本在假定的临界值0.95下方，说明这一假定尚且合理。当采用GLS方法时，GFI、AGFI和CGFI的结果都高于临界值，得出矛盾结论，说明在测量模型重度误设情况下，GLS方法得到的四种拟合指数值不能合理的反映模型拟合效果。

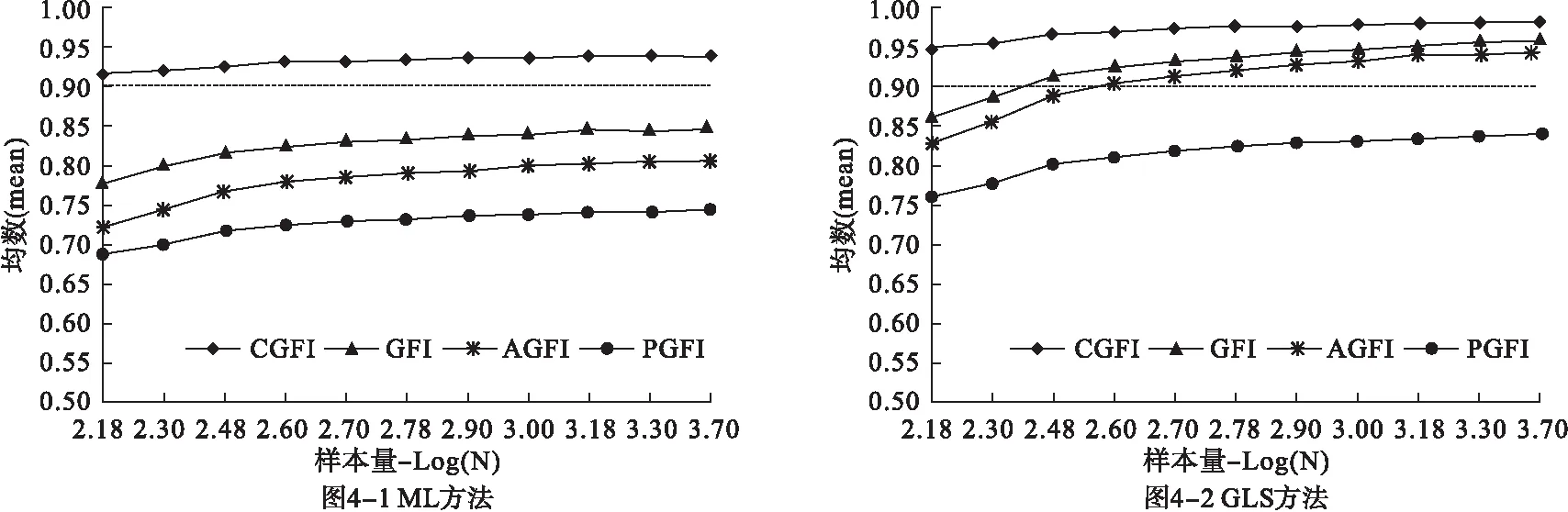
图4　测量模型重度误设下四种拟合指数在不同参数估计方法下随样本量变化的趋势

(3)结构模型误设下拟合指数的变化趋势

图5显示，结构模型轻度误设下四种指数采用ML和GLS方法时随样本量变化的趋势。两种参数估计方法的结果和测量模型轻度误设下的情况基本一致，CGFI受样本量的影响较小，且均在假定的临界值0.95之上。

图6显示，结构模型重度误设情况下四种指数分别采用ML和GLS方法时随样本量变化的趋势。两种参数估计方法的结果和测量模型重度误设下的情况基本一致，CGFI均在假定的临界值0.95之下，GLS方法的结果同样出现反常情况，不能合理反映模型拟合效果。

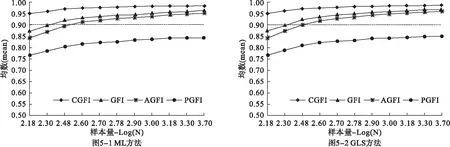
图5　结构模型轻度误设下四种拟合指数在不同参数估计方法下随样本量变化的趋势

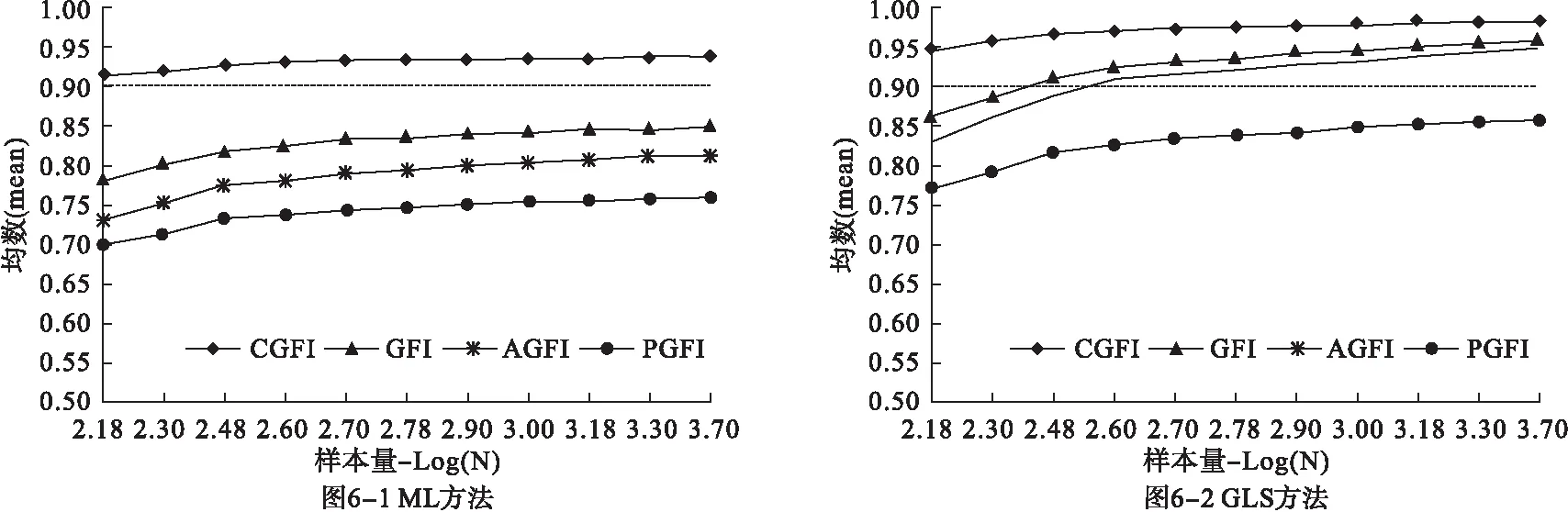
图6　结构模型重度误设下四种拟合指数在不同参数估计方法下随样本量变化的趋势

讨　　论

本研究在GFI方法基础上构建了CGFI，基于的思想是通过校正样本量纠正低估效应，通过调整自由度及待估参数对复杂模型进行惩罚。

复杂程度会影响到研究结果的稳健性[15,20]，研究指出，当SEM包含2～6个潜变量，每个潜变量包含2～6个观测变量时，所得结果相对稳健[9,20]。因此，我们在模拟研究中构建的理论模型包含4个潜变量，每个潜变量包括5个观测变量，此设定与实际情况较为接近，模拟所得结论更具一般性。

在模型误设方面，虽然有学者提出检验效能可以较为精确地量化模型误设的程度，但该方法受样本量的影响较大，将其作为量化指标并不科学[1,17]。因此，本研究从定性角度考虑两种误设程度，即轻度误设和重度误设[17-20]，并尽量保持两种测量模型和结构模型的误设程度相当，确保研究结论的可靠[18-19]。

有研究指出，数据的正态性对拟合指数的影响较小[3,18]，故本研究的模拟数据基于正态分布条件下产生，未考虑其他分布类型。

由于负方差问题(亦称Heywood问题[21-22])不可避免，我们比较了包含和不包含负方差的分析结果，发现两者差异不大，可以忽略。出现负方差的主要原因之一是模型误设，负方差率越大，说明模型误设越严重。此外，测量模型更容易发生负方差问题，模拟结果与已有研究结果一致[16,21]。

GFI和AGFI受样本量的影响较大，尤其是在样本量小于300时，还存在一定低估，这一结论与Gerbing[10]和Marsh[11]的结果一致。由于GFI和AGFI利用到样本的协方差阵信息，而协方差阵在样本量较小时不够稳定，但随着样本量的增大会渐趋稳定。CGFI是在GFI的基础上对样本量和模型复杂程度进行了校正，与其他三种指数比较，CGFI受样本量的影响有所降低，对模型误设的敏感性也有所提高。

根据模拟结果，CGFI的临界值确定为0.95，因为该临界值在不同样本量、不同参数估计方法、不同模型误设类型及误设程度时所表现的稳定性。PGFI虽然也是在GFI的基础上对模型复杂程度进行了校正，但从结果看，该指数受样本量的影响较为严重，且在不同模型情况下，均存在较严重的低估。因此，使用该指数应谨慎。在模型误设严重的情况下，GLS方法容易导致四种拟合指数值出现矛盾现象，这和Bollen和 Stine[9]的研究相吻合。

本研究虽然发现CGFI优于其他三种指数，但是并未将CGFI和RMSEA等其他常用指数进行比较研究；同时，结构方程模型复杂多样，本研究尚未考虑每个潜变量下观测变量数目及因子载荷大小的影响，因此本研究结论具有一定的局限性。

结　　论

GFI和AGFI在样本量较小时存在低估，PGFI对模型误设不敏感，且存在较为严重的低估。我们提出的CGFI方法比现有方法GFI、AGFI和PGFI均有较好的性能，可用于结构方程模型拟合效果的评价，应用时推荐临界值为0.95。