生存结局的多中介变量的中介分析方法比较*

南京医科大学公共卫生学院生物统计学系(211166)　

李清雅　魏永越　施倩雯　段巍巍　陈　峰△

【提　要】　目的　本研究以生存结局为切入点，探讨含两个中介变量时的中介生存分析模型(Aalen相加风险模型、Cox比例风险模型、加速失效时间AFT模型)，为预后的多中介变量分析方法的选择提供应用建议。方法　通过统计模拟试验，设定不同的相关系数、效应比、删失率等，从第一类错误及检验效能等方面对上述三种方法进行统计学性质评价。结果　中介变量与暴露的相关系数越大，越容易发现中介变量的中介效应；删失率与效应比对Aalen模型的影响较大，对其他两种模型的影响较小；随着删失率的降低，Aalen模型的第一类错误反而膨胀，故Aalen模型不适用于多中介变量的分析；样本量越大，三种模型的检验效能差别减小且趋于稳定。不同参数设定下，AFT模型的检验效能最大，其次为Cox模型，最后为Aalen模型。结论　AFT模型优于其他两种方法，推荐用于生存结局的多中介变量的中介分析；进行中介分析时需要足够的样本量。

中介分析(mediation analysis)是研究暴露通过中介变量对结局效应的一种方法，是研究疾病发生机制的工具之一[1-4]。在医学研究中，大量确证性研究采用中介分析，建立中介模型来进行因果关系的分析。由于研究情境复杂，常用的考虑单个中介变量的中介模型往往不能满足实际问题的分析需求，需要考虑多个中介变量才能更清晰地解释暴露对结局的效应，这方面的研究越来越受到理论界的关注[5-7]。特别在生存分析中，多中介模型的研究和应用刚刚起步[8，9]。

目前，针对生存结局，常用的三种针对多个中介变量的生存模型分析方法有：Aalen相加风险模型，Cox比例风险模型和加速失效时间(AFT)模型。三种模型分别描述了特定尺度下的中介效应，Aalen相加风险模型是基于风险之差，Cox模型基于对数风险之比，AFT模型基于平均生存时间之比。然而，至今尚无报道对以上三种方法进行比较评价。

本研究以生存结局为切入点，探讨两个中介变量的中介生存分析模型，通过统计模拟试验，设定不同的相关系数、效应比、删失率等，从第一类错误及检验效能等方面对上述三种方法进行统计学性质评价，为预后的多中介变量的中介分析方法的选择提供应用建议。

原理与方法

用S表示个体的暴露，M1和M2表示两个中介变量，Y表示结局变量，S、M1、M2和Y的因果关系见图1。

图1　两中介变量的因果关系图

首先，定义结局变量Y是关于疾病发展时间T的函数，Y=H(T)。Y(s,m1,m2)是将暴露S、中介变量M1和中介变量M2的值分别设为s、m1、m2时反事实(指在不同条件下有可能发生但违反现存事实)的结局变量的值；M2(s,m1)是将暴露S、中介变量M1的值分别设为s、m1时反事实的中介变量M2的值；M1(s)是将暴露S的值设为s时反事实的中介变量M1的值。将自然直接效应和间接效应扩展到两中介变量模型，定义如下三个特定路径效应[10-11]：

ΔS→Y=Y(s1,M1(s0),M2(s0,M1(s0)))-Y(s0,M1(s0),M2(s0,M1(s0)))

ΔS→M2→Y=Y(s1,M1(s0),M2(s1,M1(s0)))-Y(s1,M1(s0),M2(s0,M1(s0)))

ΔS→M1Y=Y(s1,M1(s1),M2(s1,M1(s1)))-Y(s1,M1(s0),M2(s1,M1(s0)))

(1)

1.Aalen相加风险模型

分别构建M1和M2的线性回归模型：

(2)

(3)

(4)

其中λi表示个体i发展成某种疾病的风险；λ0(t)是基线风险。

在风险差异的尺度下重新表达特定路径效应(PSEs)：

(5)

2.Cox比例风险模型

相加风险模型假设风险是被线性预测的，与相加风险模型不同，Cox模型假设风险是呈指数(对数风险尺度上呈线性)被预测的：

(6)

在对数风险比的尺度下重新表达特定路径效应(PSEs)：

(7)

3.加速失效时间(AFT)模型

与Cox比例风险模型类似，以加速失效时间(AFT)模型建立生存结局的模型：

(8)

其中ε是服从极值分布的随机变量，是尺度参数。在平均生存时间比的尺度下重新表达特定路径效应(PSEs)：

(9)

可通过重抽样的方法计算ΔAalen、ΔCox和ΔAFT的方差和可信区间[12]。

模拟试验

1.模拟数据的产生

(1)指定ΔS→Y，即对应λS(或γS,θs)值；

(2)指定样本量(N)、S与M1、S与M2、和M1与M2的相关系数r1、r2和r3，可产生多元标准正态分布随机数S、M1和M2；此时r1、r2和r3即为δS,αS和αM值；

(3)指定效应比R，即间接效应/直接效应，可知ΔS→M1Y，根据公式可计算求得λM1值；

(4)把变量S、M1、M2和设定的系数代入指数回归模型的风险函数λi=exp(λSSi+λM1M1i+λM2M2i)，基于指数分布随机产生生存时间；

(5)根据样本量(N)和删失率(cen%)随机产生截尾，1代表死亡，0代表删失。

(6)设λM2=0，比较方法的第一类错误；设λM2= 1，比较方法的检验效能。

模拟试验中考虑的影响因素包括S与M1、S与M2、M1与M2的相关系数，效应比、删失率、样本量等。中介变量与中介变量以及中介变量与暴露之间的关系越复杂，越难将中介变量的效应从暴露对结局的效应中分解出来，会影响中介分析的检验效能。由于生存资料的删失率越高，模型预测越不准确，模拟试验时删失率取值70%以下。参数设置见表1。

表1　模拟试验参数设置情况

2.模拟试验流程

(1)根据不同的参数设置产生模拟数据；

(2)对产生的同一模拟数据分别用三种方法进行分析，提取相关结果，包括三个特定路径效应(PSEs)的点估计、区间估计(95%CI)及假设检验P值；

(3)重复(1)～(2)步骤1000次，对1000次的结果进行汇总，得到三种方法的第一类错误和检验效能。

结　　果

1.第一类错误

(1)删失率对第一类错误的影响

在Aalen模型中，当相关系数r1固定时，随着相关系数r2的增大，第一类错误逐渐膨胀，并超过0.05；当相关系数r1、r2均固定时，随着删失率(cen%)的增加，第一类错误逐渐减小。

在Cox模型中，当相关系数r1固定时，随着相关系数r2的增大，第一类错误逐渐增大且趋于0.05；当相关系数r1、r2均固定时，随着删失率(cen%)的增加，第一类错误逐渐减小。

在AFT模型中，结果与Cox模型类似。当样本量较大(N=500)时，三种模型的第一类错误受删失率的影响很小。

图2显示了当M1与M2的相关系数r3=0，效应比R=0.1，删失率(cen%)为70%时，三种模型的第一类错误的比较。横坐标为两个中介变量(M1、M2)与暴露(S)的相关系数(r1、r2)的组合，纵坐标为第一类错误。

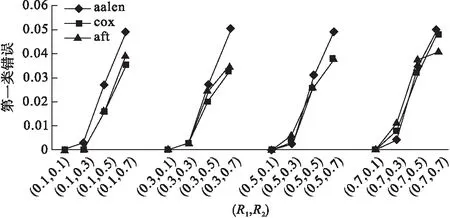
图2　三种模型的第一类错误的比较

(2)M1与M2的相关性对第一类错误的影响

当删失率(cen%)为70%，效应比R为0.1时，随着M1与M2的相关系数r3逐渐增大，三种模型的第一类错误的差别逐渐减小且趋于稳定。

(3)样本量的影响

总体来讲，随着样本量N的增加，不同情景下，三种模型的第一类错误逐渐趋于稳定。Aalen模型的第一类错误略有膨胀，其他两种模型的第一类错误趋于设定的0.05。

表2显示了当M1与M2的相关系数r3=0，效应比R=0.1，删失率(cen%)为70%时，样本量N对三种模型的第一类错误的影响。

2.检验效能

(1)删失率对检验效能的影响

在Aalen模型中，当M1与S的相关系数r1固定时，随着相关系数r2的增大，检验效能出现先增大后减小的趋势；当相关系数r1、r2均固定时，随着删失率(cen%)的增加，检验效能逐渐减小，当删失率(cen%)为70%时，检验效能最小。

在Cox模型中，当M1与S的相关系数r1固定时，随着相关系数r2的增大，检验效能出现先增大后减小的趋势；当相关系数r1、r2均固定时，随着删失率(cen%)的增加，检验效能逐渐减小，删失率在30%以下时，检验效能的差别很小。

在AFT模型中，当M1与S的相关系数r1固定时，随着相关系数r2的增大，检验效能出现先增大后减小的趋势；当相关系数r1、r2均固定时，随着删失率(cen%)的增大，检验效能略减小，同时检验效能普遍较高(大于0.8)，当相关系数r1、r2均等于0.7时，检验效能出现低值，对这种情况需要做进一步研究。

当样本量较大(N=500)时，三种模型的检验效能受删失率的影响很小。

图3显示了当M1与M2的相关系数r3=0，效应比R=0.1，删失率(cen%)为70%时，三种模型的检验效能的比较。横坐标为两个中介变量(M1、M2)与暴露(S)的相关系数(r1、r2)的组合，纵坐标为检验效能。

表2　样本量对三种模型的第一类错误的影响

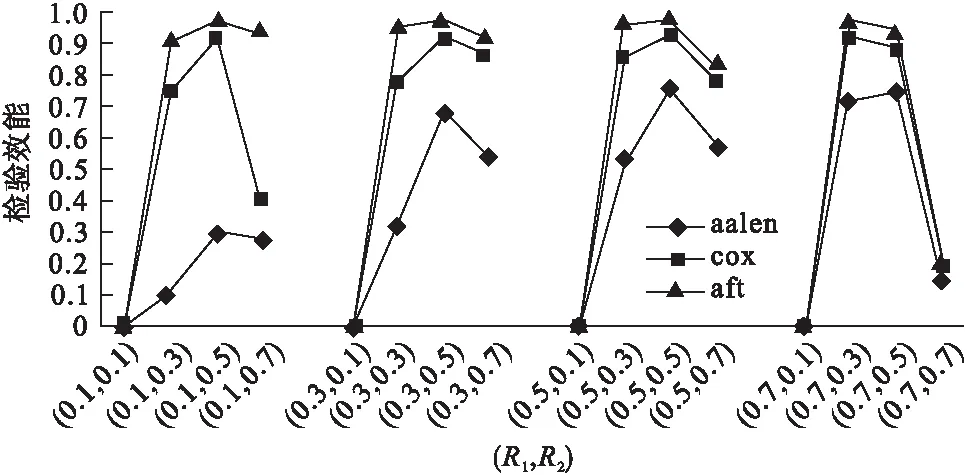
图3　三种模型的检验效能的比较

(2)M1与M2的相关性对检验效能的影响

随着中介变量M1与M2的相关系数r3的增大，三种模型的检验效能呈减小的趋势。三种模型的检验

效能的大小排序均为：AFT模型>Cox模型>Aalen模型，Aalen模型的检验效能偏低。

(3)样本量对检验效能的影响

总体来讲，随着样本量N的增加，不同情景下，三种模型的检验效能逐渐增大，且差距逐渐减小，趋于稳定。当样本量较小(N=100)时无法检验出来的效应；样本量增大时，各模型的检验效能也随之增大。当样本量较大(N=500)且M1与S的相关系数r1较大时，三种模型的检验效能基本一致。

表3显示了当M1与M2的相关系数r3=0，效应比R=0.1，删失率(cen%)为70%时，样本量N对三种模型的检验效能的影响。

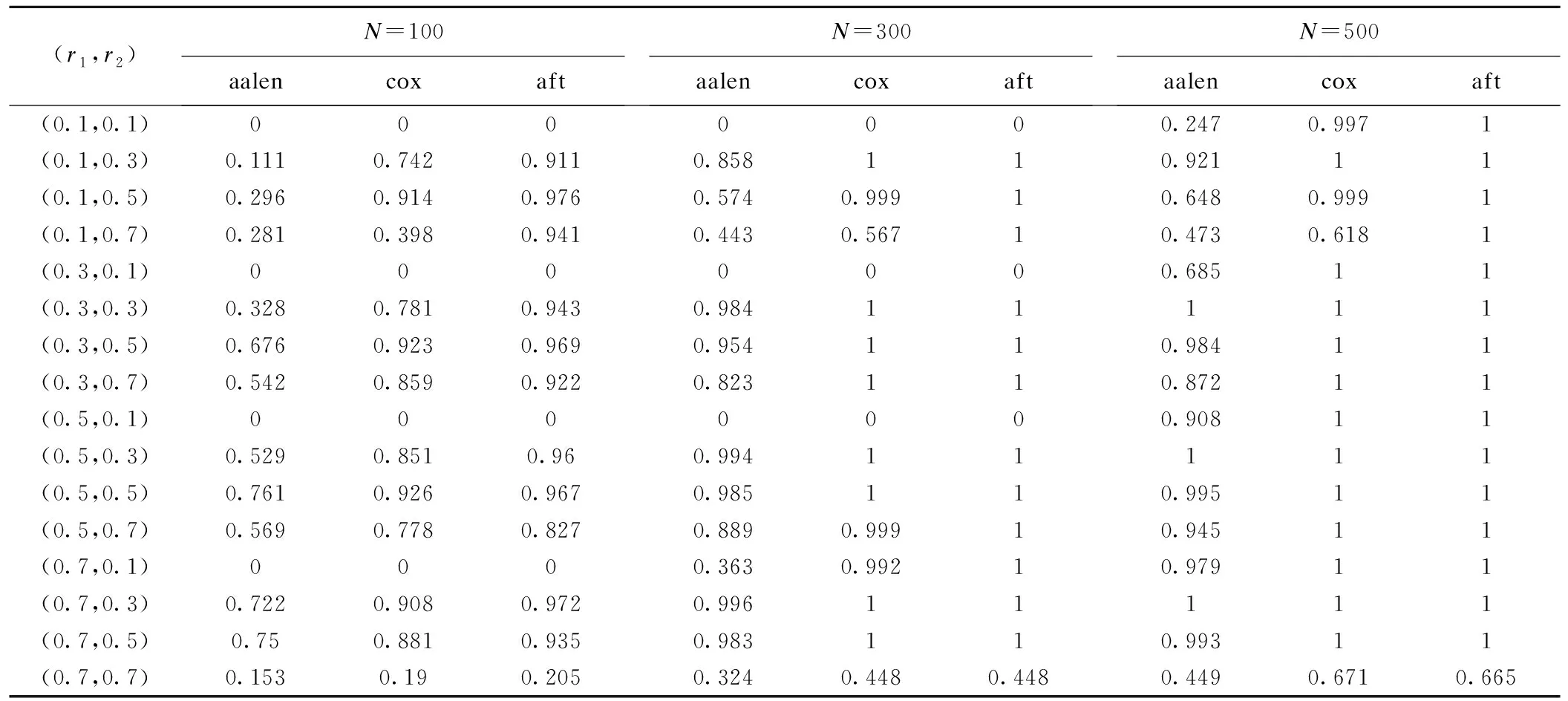
表3　样本量对三种模型的检验效能的影响

讨　　论

本研究主要讨论了两个中介变量的特定路径效应(PSEs)，以及两中介变量之间不存在交互作用的情况。随着中介变量的增多，中介变量与中介变量以及中介变量与暴露之间的影响必定更加复杂，此时对模型的构建和方法的选择需要做进一步深入的研究。

1.暴露与中介变量间的相关对结果的影响

当M1与S的相关系数r1固定时，随着M2与S的相关系数r2的增大，三种模型的检验效能均出现先增大后减小的趋势，原因是在小样本量(N=100)的条件下，M2与暴露S相关性过高，难以从暴露对结局的效应中分解出M2对结局的效应。当样本量扩大至500时，这种趋势不再存在，三种方法的检验效能均增大并趋于稳定，提示中介变量与暴露的相关性越高，需要更大的样本量才能检验出中介效应。

2.中介变量间的相关对结果的影响

当暴露与中介变量间的相关系数固定时，随着中介变量间的相关系数r3的增大，三种模型的检验效能呈减小的趋势。中介变量间的相关性越高，两个中介变量对结局的效应发生重叠，越难将两个中介变量的中介效应区分开来，也就越难发现中介变量M2对结局Y的效应，此时可通过增大样本量，以提高检验效能。

3.样本量对结果的影响

模拟试验结果显示，无论在何种情况下，随着样本量的增加，检验效能趋于稳定。即使在暴露与中介变量相关性较高的情况下，也能保持足够的检验效能。这说明，进行中介分析，必须要有足够的样本量。

4.删失率对结果的影响

随着删失率的增加，检验效能逐渐减小，实际数据的分析过程中会遇到很多删失率较大的数据，对于高删失率的数据，在方法的选择上要更加慎重。有研究显示，对于大样本(≥500)或删失率较小(≤30%)的数据，Cox模型和AFT 模型的有效性及偏倚性相近，分析结果均较为可靠。对于样本较小(300～400)或删失率较高(40%～60%)的数据，AFT模型的分析结果似乎更为可靠，此时应首先考虑采用该模型进行分析。但当样本量不足200或删失率超过70%时，两类模型的适用性都不佳。当出现样本量不足或删失率过高的情况下，可考虑选择其他模型对生存结局进行分析。

5.对三个模型的评价

在Aalen相加风险模型、Cox比例风险模型和加速失效时间(AFT)模型下的多中介变量的中介分析描述了特定尺度下的中介效应，Aalen相加风险模型是基于风险差异，Cox模型基于对数风险比，加速失效时间(AFT)模型基于平均生存时间比，模型解释时需要注意。三种模型下的解析表达式都可以通过因果关系图上各个箭头对应的效应参数被直观地解释。

通过模拟试验发现，随着删失率的降低，Aalen模型的第一类错误膨胀。Cox模型的解析表达式只有在结局不常见的假设下才能得到，是其应用的局限性。不同参数设定下，AFT模型的检验效能最大，其次为Cox模型，最后为Aalen模型。AFT模型优于其他两种方法，推荐用于生存结局的多中介变量的中介分析。同时，进行中介分析时需要足够的样本量，才能发现多个中介变量的中介效应。