从反比例函数到一般双曲线图像的性质

颜美玲

(浙江省杭州外国语学校　310023)

文[1]研究了同一坐标系中系数互为倒数的正、反比例函数图像性质，得到(以k>0为例)：

文[1]通过添加辅助线，发现了两个等腰三角形进而结合解析法证明了定理1.读后,笔者不由地感叹结论的优美和证法的巧妙.与此同时，笔者开始思考：反比例函数与正比例函数的比例系数不互为倒数时有类似的性质吗？对于一般读者，还能用其它一般的方法证明吗？一般双曲线有类似的性质吗？带着这些问题，笔者进行了一番探究，收获颇丰.现与各位同行讨论.

1　问题探究

问题1可否不添加辅助线,利用纯解析法证明有关结论呢？

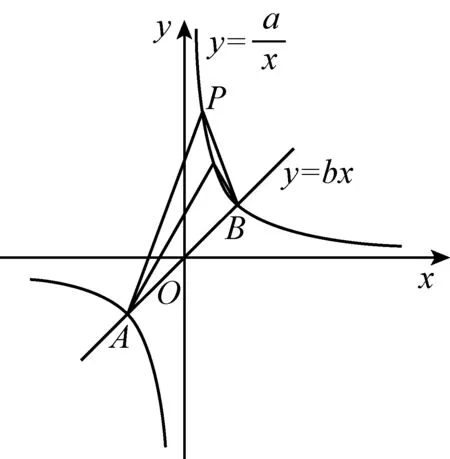
图1

经过研究,我们发现纯解析法是可行的，并且推广了定理1得到如下结论：

(1)当P,Q在直线AB同侧时, 若P,Q在同一支上，则∠PAQ=∠PBQ(如图1); 若P,Q在不同支上，则∠PAQ+∠PBQ=180°(如图2).

图2

(2)当P,Q在直线AB异侧时, 若P,Q在同一支上，则∠PAQ+∠PBQ=180°; 若P,Q在不同支上，则∠PAQ=∠PBQ.

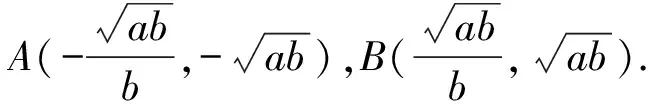
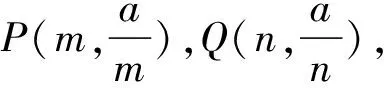
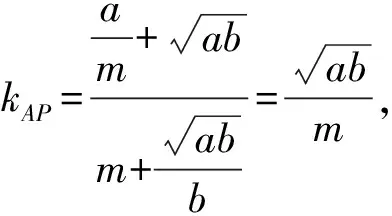
记直线AP,AQ夹角为θ,直线BP,BQ夹角为α,则

通过整理可得tanθ=tanα.

结合P,Q的位置，易知 (1)(2)结论成立.

注当a<0,b<0时，上述结论仍成立.

问题2一般的双曲线是否有类似的结论呢？

借助几何画板，我们发现对于一般的双曲线上述结论不一定成立.而反比例函数图像的两条渐近线是互相垂直的，于是我们猜想两条渐近线垂直的双曲线是否也有类似的结论呢？最终我们证明了此猜想是正确的，得到以下结论.

图3

定理3设A,B是双曲线x2-y2=k2(k>0)与正比例函数y=bx的两个交点,P,Q是双曲线上的两点(P,Q均不与A,B两点重合),则有

(1)当P,Q在直线AB同侧时,若P,Q在同一支上，则∠PAQ=∠PBQ(如图3);若P,Q在不同支上，则∠PAQ+∠PBQ=180°.

(2) 当P,Q在直线AB异侧时,若P,Q在同一支上，则∠PAQ+∠PBQ=180°;若P,Q在不同支上，则∠PAQ=∠PBQ.

分析对于这个结论，文[1]中添加辅助线的方法已然不适用，而定理2中用斜率求夹角的方法在理论上是可行的，但计算量太大,所以我们不能直接利用几何性质或定理2的解析法去证明，而是考虑将等轴双曲线上的问题转化为反比例函数图像上的问题.为此，先引入坐标系旋转的有关结论:若直角坐标系绕原点顺时针旋转角θ,(x,y)是原直角坐标系下点的坐标,(x′,y′)是新直角坐标系下点的坐标,则有

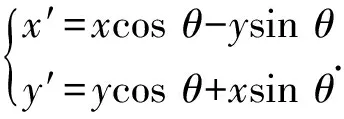
当θ=45°时,

问题3双曲线的有关面积定值问题

对于反比例函数我们知道有以下两个与面积有关的性质.

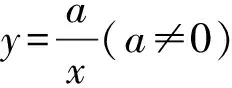
(此处证明过程省略，读者可自证.)

那么我们是否可以考虑双曲线有关面积的性质呢?

由定理3的分析我们知道，对于等轴双曲线，当坐标系绕原点顺时针旋转45°时，在新坐标系下它是反比例函数，从而我们可得如下两个性质.

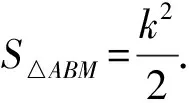
图4

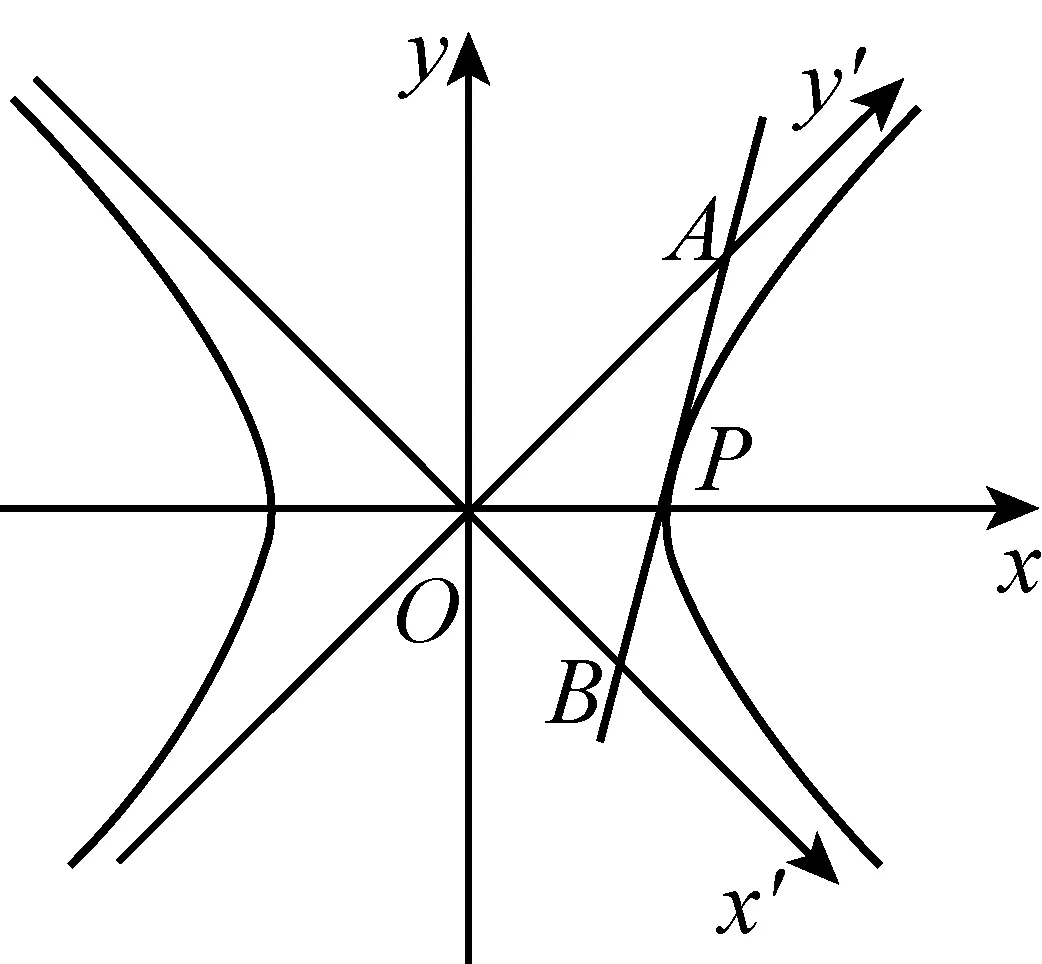
图5

定理5如图5,P为等轴双曲线x2-y2=k2(k>0)上任意一点，过P点的切线与双曲线的两条渐近线交于A,B两点，则S△AOB=k2.

简析如图4,5,将原坐标系绕原点顺时针旋转45°就可利用引理1，2证明上述两个定理.

引理3[2,3]

(1)A,B,C三点不共线当且仅当A′,B′,C′三点不共线，并且S△ABC=mnS△A′B′C′.

(2)AB∥CD当且仅当A′B′∥C′D′.

(3)原曲线上P点的切线经过伸缩变换后是新曲线中P′的切线.

其中A′,B′,C′,D′,P′是A,B,C,D,P在伸缩变换T下的象.

根据定理4、5以及引理3，我们不难得到一般双曲线的有关面积的性质.

2　结论和思想方法归纳

(1)文[1]的定理1为本文定理2的特殊情形.一方面定理2中取ab=1就是文1中的定理1的内容,另一方面文[1]中定理1的结论限定在“P,Q在双曲线的同一支上”的条件，而本文定理2适用于“P,Q在双曲线的同一支上或不同支上”.另外，定理2的证明方法更加直观简洁.

本文除了推广文[1]的结论外，最主要的也是最有意义的是提供了处理一般双曲线问题的一种新思路：通过伸缩变换把一般的双曲线上的问题转化为等轴双曲线上的问题,接着通过旋转变换把等轴双曲线上的问题转化为反比例函数图像上的问题，最后就可利用反比例函数图像的有关性质加以解决.这样处理有两个好处——一是可预先猜想结论，二是避免繁琐的计算.