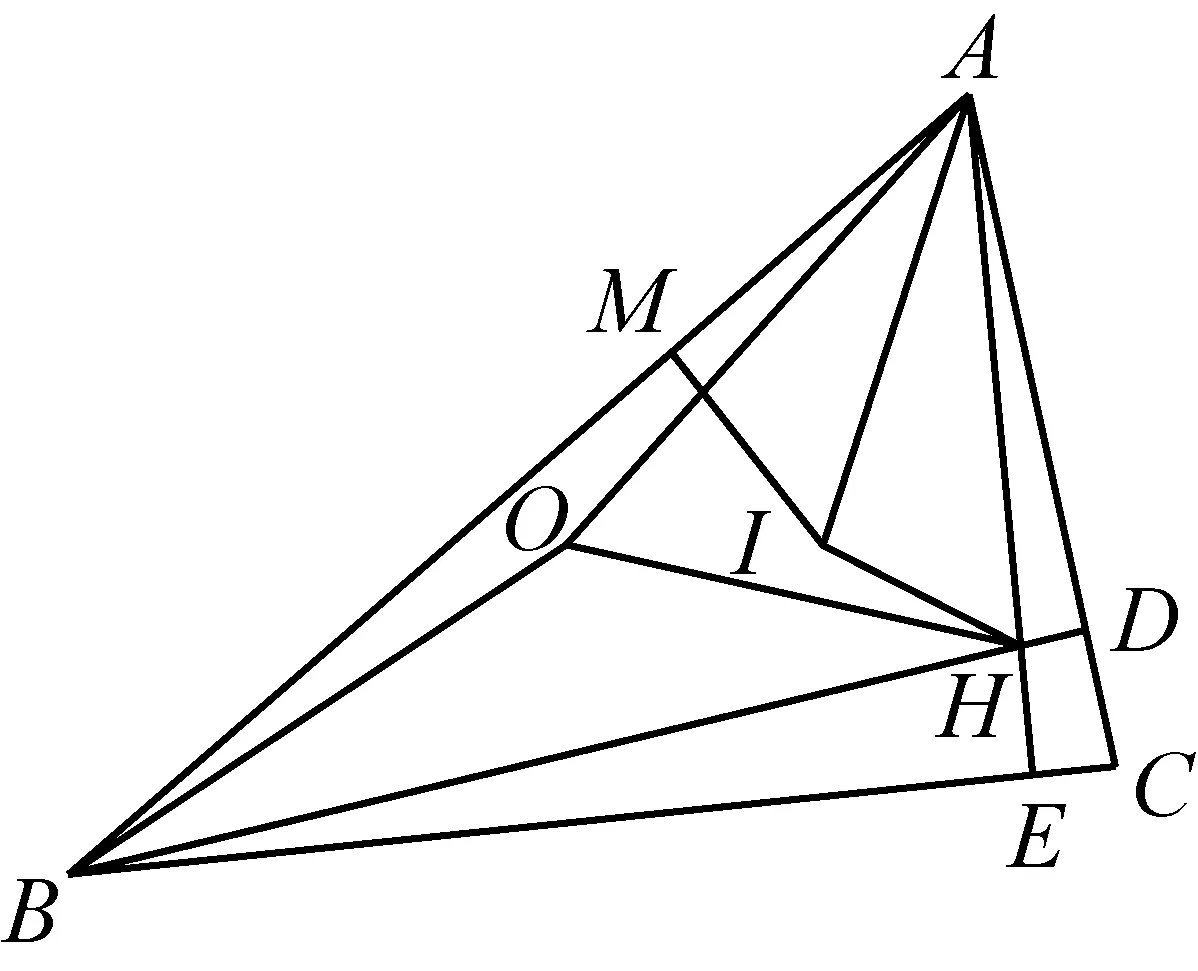
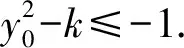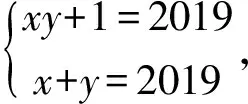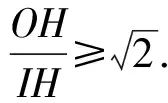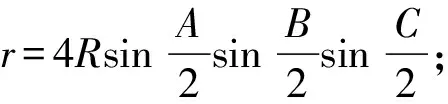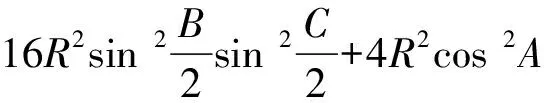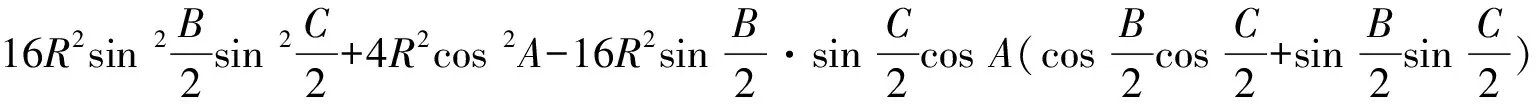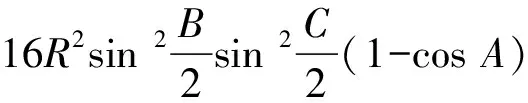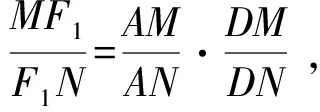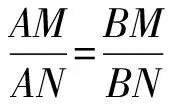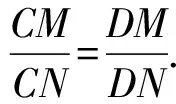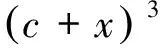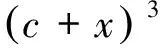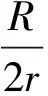数学问题解答

(解答由问题提供人给出)

(x+y)2=2019(xy+1),

2411设x,y为正整数,x2+y2-2017xy>0且不是完全平方数,求x2+y2-2017xy的最小值.

(四川省成都七中方廷刚610041)

解记x2+y2-2017xy=k,其中k不是完全平方数.首先证明k≥2019.

设(x0,y0)是方程

x2+y2-2017xy=k

①

的使得x0+y0最小的一组正整数解.

不妨设x0≥y0.

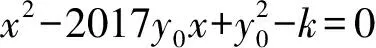
②

由前式知x1∈Z,由k不是完全平方数知x1≠0.

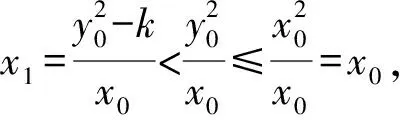
故x1+y0

故只能x1<0,

于是

另一方面,令x2+y2-2017xy=2019得

(x+y)2=2019(xy+1),

可解得(x,y)=(2018,1)或(1,2018).

于是所求最小值为2019.

(安徽省安庆市岳西县汤池中学杨续亮246620)

证明在锐角△ABC中作两条高AE、BD交于点H，O为外心，I为内心，连接AO，BO，OH，IA，IH，过I作AB的垂线交AB于点M.设锐角△ABC的外接圆半径为R，内切圆半径为r，

在Rt△AHD中，

=2RcosA，

所以 ∠OAH=|A-∠EAC-∠BAO|

=|B-C|，

在△OAH中，由余弦定理可知

OH2=OA2+AH2-2OA·AHcos ∠OAH，

所以

OH2=R2+4R2cos2A-4R2cosAcos (B-C)

=R2-4R2cosA(cos (B-C)-cosA)

=R2-4R2cosA(cos (B-C)+cos (B+C))

=R2-8R2cosAcosBcosC，

根据正弦定理可得

2R2sinAsinBsinC=Rr(sinA+sinB+sinC)，

又由三角恒等式

又在△AMI中，

而 ∠IAH=|A-∠EAC-∠BAI|

在△IAH中，由余弦定理可知

IH2=AI2+AH2-2AI·AHcos ∠IAH，

所以

IH2=AI2+AH2-2AI·AHcos ∠IAH

+4R2cosA(cosA-sinBsinC)

-4R2cosA(cos (B+C)+sinBsinC)

-4R2cosAcosBcosC

=2r2-4R2cosAcosBcosC，

所以OH2-2IH2=R2-4r2；

由欧拉定理OI2=R2-2Rr可得R≥2r，

所以OH2-2IH2=R2-4r2

=(R+2r)(R-2r)≥0，

2413设AB和CD为圆O的两弦，AB的延长线与CD的延长线交于点E，AD与CB交于点F，以EF为直径的圆O′与圆O交于点P和Q，证明：圆O和圆O′ 在交点P或Q处的切线互相垂直.

(河南省辉县市一中贺基军453600)

证明如图，自点E引圆O的切线EM和EN，切点为M，N，连接MN.

设AD与MN交于点F1，CB与MN交于点F2，连接AM，BM，CM，DM及AN，BN，CN，DN. 记圆O的半径为R.

又DM=2Rsin ∠MAF1,

DN=2Rsin ∠NAF1，

①

②

根据以上两个等式及EM=EN得

③

④

即MF1=MF2，

这表明F1,F2两点重合，进而可知AD,MN,CB三线共点，点F在MN上.

连接PO,PO′及OM,OE,OO′，

其中OE为MN的中垂线，垂足为G.

O,O′,E这三点或共线或不共线，总有

O′O2=O′E2+OE2-2O′E·OE·cos ∠O′EO

=O′E2+OE2-FE·OE·cos ∠FEG

=O′E2+OE2-OE·GE

=O′E2+OE2-ME2

=O′E2+OM2

=O′P2+OP2，

因此O′P⊥OP，从而可知圆O在交点P处的切线为PO′，圆O′ 在交点P处的切线为PO，二者互相垂直.

同理，上述两圆在另一交点Q处的切线互相垂直.

2414已知a,b,c>0,a+b+c=3,求证：

(陕西省咸阳师范学院基础教育课程研究中心安振平712000)

证明所证不等式等价于

∑(1+ab)(1+b)(1+c)

≤3∏(1+a),

(*)

因为∑(1+ab)(1+b)(1+c)

=∑(1+ab)(1+b+c+bc)

=∑(1+ab)(1+bc)+∑(1+ab)(b+c)

=3+2∑bc+abc∑a+2∑a+∑ab2+3abc,

3∏(1+a)=3+3∑a+3∑bc+3abc,

所以，不等式(*)等价于

abc∑a+∑ab2≤∑a+∑bc,

等价于

27abc+9∑ab2≤(∑a)3+3∑a∑bc,

等价于∑a3+2∑a2b≥3∑ab2.

不妨设

c=min{a,b,c},a=c+x,b=c+y,x≥0,y≥0.

于是

P=∑a3+2∑a2b-3∑ab2

3∑(c+x)(c+y)2.

3∑(c+x)(c+y)2

=2c[(x-y)2+xy]+[x3+2x2y-3xy2+

y3].

记Q=x3+2x2y-3xy2+y3,

当y=0时，Q=x3≥0;

当y>0时，

(t≥0)

求导，得

f′(t)=3t2+4t-3

从而P=∑a3+2∑a2b-3∑ab2≥0,获证.

(四川省西充中学李光俊637200)

解引入常数λ>0

t3-2t-1=0

即(t+1)(t2-t-1)=0，

2018年4月号问题

(来稿请注明出处——编者)

(浙江省慈溪市慈溪实验中学华漫天315300)

2417四边形ABCD的边AD、BC相交于点P，AB与CD不平行，△ABP、△CDP的外心分别为O1、O2，垂心分别为H1、H2，O1H1、O2H2的中点分别为E1、E2，过E1、E2分别作CD、AB的垂线.证明：这两条垂线与H1H2三线共点.

(江西省高安市石脑二中王典辉330818)

(n≥3,n∈N)

(江苏省常熟市中学查正开215500)

2419在△ABC中,R,r分别是△ABC的外接圆半径和内切圆半径,∠BAC的平分线AD与△ABC的外接圆相交于点D,AD与BC相交于点E,则

(天津水运高级技工学校黄兆麟300456)

2420设△ABC中的三边长分别为a,b,c，外接圆和内切圆半径分别为R,r，则

(1)

(河南质量工程职业学院李永利467000)