“两面” 何须三刀①
——刍议高中数学中的“双变”问题
王爱军
(江苏省姜堰中学 225500)
1 问题的提出
高中数学解题中,同学们常常会碰到“双变问题”,不少同学面对双重压力,心慌气短、手忙脚乱,误打瞎撞,错误率极高.“如果只有一个‘量’在变,我还能勉强应付,但对于两个‘量’都在变,我往往顾此失彼,晕头转向……”(学生语).波利亚在《怎样解题》一书中指出,弄清问题”是实现成功解决问题的第一步.现在,我们面临的问题是如何基于学生“单变尚可,双变犯难”的数学现实,引导学生实现突破?
2 突破:“二”即是“一”
数学来源于生活,提炼于生活,并引领着生活,那么我们能否从生活中寻找双变问题的解题灵感呢?其实,双变问题无异于“脚踩两只船”,顾此失彼,情理之中,要独善其身必须用心专一、从一而终,基于这种想法,解决双变问题不也可采取“我的眼里只有你”的策略,专攻其一,逐个突破,拾级而上吗?即所谓“二便是一”.下面就以高中数学中的几个典型的双变问题加以阐述.
2.1 双变量问题: 退“二”进“一”,以退为进
2.1.1主元思想:视“二”为“一”
题1若不等式bx+c+9lnx≤x2对任意的x∈(0,+∞),b∈(0,3)恒成立,则实数c的取值范围是.
分析本题中涉及两个变元,在处理的过程中应先以一个较为容易研究的变量为主元构建函数关系,通过研究此函数的性质来解决问题,所以首先选择b为主元来研究问题.
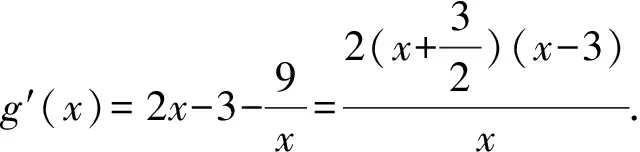
点评视“二”为“一”的主元思想突显了“脚踩两只船”时,优选顺序,逐一突破的“减元”的解题策略.
2.1.2整体思想:化“二”为“一”
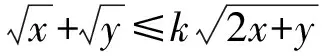

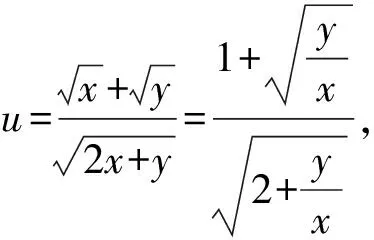
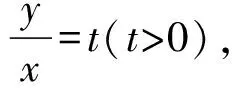
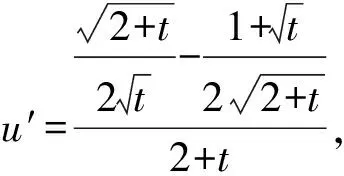
令u′=0得t=4,且t∈(0,4)时,u′>0;
t∈(4,+∞)时,u′<0.
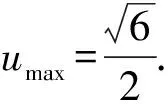
无论是化“二”为“一”的整体思想,还是视“二”为“一”的主元思想都采取的是退二进一的转化策略,实现了双变量到单变量的有效转化.当然,处理二元变量问题有时也可直接借助不等式或几何知识来解决,比如线性规划问题就是利用图解法解决二元变量最值问题的一类题型,它是把代数形式的二元变量转化成一种图形语言加以处理,从这个角度来说,也就实现了“二即是一”.当然,本题也可借助不等式或几何知识来解决.
2.2 双动点问题:动静变换、以静制动
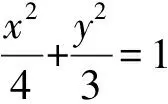
分析此题涉及双动点,要突破“双动”,首先必须以静制动,化“双”为“单”,然后再各个击破.

图1
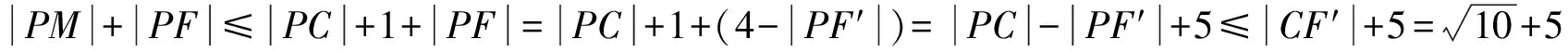
点评“双动点”问题可以通过先将动点1视为定点研究出动点2运动时所求问题的最值1,然后再处理动点2运动时最值1的最值,从而最终得出所求问题的最值,其解题策略是视动为静,化“双动”为“单动”,再逐一突破,最后利用函数知识或几何性质求出“双动点”问题的最值.
2.3 “双层”最值问题:抽丝剥茧、内外兼修
题4函数f(x)满足f(x)=x2-2(a+2)·x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=________.
分析本题要求两个函数值中的较大者(或较小者)中的最值,其解题策略是厘清层次,由内到外,抽丝剥茧,我们只需先求出H1(x)=max{f(x),g(x)}、H2(x)=min{f(x),g(x)}的表达式或函数图像,再结合函数及其图像分别求出它们的最值A、B.
解令h(x)=f(x)-g(x)
=x2-2(a+2)x+a2-[-x2+2(a-2)x-a2+8]
=2x2-4ax+2a2-8
=2(x-a)2-8.
①由h(x)=0得2(x-a)2-8=0,解得x=a±2,此时f(x)=g(x);
②由h(x)>0,解得x>a+2,或x
③由h(x)<0,解得a-2 综上可知: 作出函数H1(x)、H2(x)的图像(如图2),结合图像易得 A=g(a+2)=-[(a+2)-(a-2)]2-4a+12 =-4a-4, B=g(a-2)=-4a+12, 所以A-B=-4a-4-(-4a+12)=-16. 图2 点评“双层”最值问题可以通过由内到外分层研究对应目标函数,即先求出“内层”函数的最值,得到“外层”函数,从而最终构建了目标变量的函数,利用函数知识解决问题.“双层”最值问题的解题策略是循序渐进、分层实施、逐次突破. 点评“双层”最值问题也可以通过分层构建目标变量的不等关系,利用不等式的性质求出“双层”问题的最值. 高中数学中涉及到的双变问题不仅仅有双变量、双动点、双层最值等问题,还常涉及以下双变问题: (1)双向问题:锁定方向、择一而终 题6A、B、C、D、E五人站成一圈传球,每人只能传给他的邻人(左、右不限),求A传出(算第一次)后经过十次传球又回到A的概率. (2) 双重“身份”问题:整二合一 题7已知等差数列{an}中,a3=2,a5=6,若正整数n1,n2,…,nt,…(t∈N*)满足5 (3) 双限问题:①去杂法:无“限”驰骋、锄“奸”务尽②直接法:突出主次、先后兼顾 题8有5人排成一排,要求其中甲不排在排头且乙不排在排尾,则有多少不同的排法? (4)双时(约会)问题:构建几何模型 题9甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头.假设它们在一昼夜内任何时刻到达码头是等可能的.如果甲船的停泊的时间是2小时,乙船停泊的时间是1小时,求两船到达码头均不需要等待码头空出的概率. (5)双段(分段)函数问题:先分后合、合二为一 (6)双层复合问题 (7)二项分布问题 题12某人每次射击命中目标的概率为0.8,现连续射击3次,求击中目标的次数X的数学期望和方差. “不断地变换你的问题”、“我们必须一再变化它,重新叙述它,变换它,直到最后成功地找到某些有用的东西为止.”(波利亚)事实上,无论是哪种双变问题,我们一般都可以采用明确主次,变“二”为“一”,逐次突破的理念加以解决,其所谓“二即是一”. 双变问题源自单变,尚若在单变问题中,我们动静变换,化静为动,或者定变互换,化定为变,那单变就生长为双变,有时甚至也可直接由单变生长为双变. 题13在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为() 本题是2007年江苏省高考数学试卷选择题压轴题.据高考试卷命题组后来发布的命题情况说明了解到,本题就是由如下问题“生长”而来. 在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域A的面积为() “二即是一”,其要义包含两个层面:一、双变问题的突破,其本质就是有效实现双变至单变的转化,达到未知到已知的飞跃;二、追根溯源,双变问题由单变孕育、生长而来.因此,“二”从“一”中来,必要回到“一”中去,“二”即是“一”,和谐统一.著名的数学家、莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出:“解题就是把要解的题转化为已经解过的题”.数学的解题过程,就是从未知向已知、从复杂到简单的化归转换过程.因此,当我们面对“双变”问题的挑战时,我们不必惊慌失措,也不必“脚踩两只船”,我们只需把持“重心”,采取变“二”为“一”的消元策略,实现由“双变”到“单变”的有效转化,从而不难达到解决此类问题的目的.可以说,“两面”,何须三刀?以思想的“快刀”宰乱麻足矣! 数学来自生活,作用于生活,引领着生活.双变问题的突破也启示着同学们:当人生中,面对纷繁复杂的挑战时,我们应当厘清主次,抓住矛盾的主体,排除干扰,集中力量解决好问题的最主要矛盾,进而逐一突破,实现成功.因此,引领学生突破双变问题,其既是知识的传授,也是思想的启发,更是学会生活的启迪.这难道不就是我们数学教育追求的最本质、最重要的价值吗?




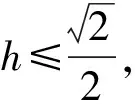
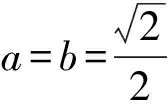

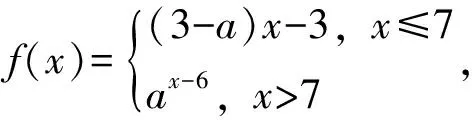

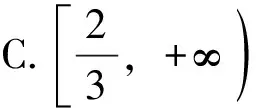
3 溯源:“二”生长于“一”
4 结语:“二”即是“一”,和谐统一

