中学数学“用频率估计概率”问题及设计建议

李红云　朱文芳　伍春兰　张淑梅

(1.北京师范大学　100875；2. 北京教育学院　100120)

1　问题提出

用频率估计概率是中学统计与概率的重要内容之一，对频率与概率关系的认识是理解概率意义、体会随机性的重要载体，是理解统计推断的基础. 然而通过对一些中学数学教师进行访谈、学生调查及我们听过很多频率估计概率的课，发现存在一些问题：①不做随机试验:由于考试评价或教师自身对频率稳定性并不理解等原因，实际教学中并不讲这个内容，以投掷一枚质地均匀的硬币为例，当出现正面向上次数不等于背面向上次数时，教师往往不知如何向学生解释；②试验设计引起误解：在教学这个内容时，通过随机试验：一列不断增加的试验次数所对应频率的“规律性”，并直接用教材中的总结语言“随着试验次数的增加，频率总是或都在一个常数附近摆动，即频率具有稳定性”来解释，往往容易导致学生的误解：频率稳定到一个常数是确定的事情. 这也与我们对学生调查的结果一致：硬币正面向上次数为43，背面向上次数为37时，很多学生都认为正面向上、背面向上可能性不同；③初高中随机试验发展：初、高中都有用频率估计概率，两个学段的侧重点是什么？发展点是什么？也是一线教师存在困惑的地方.

那么如何理解频率稳定性？设计什么试验活动能让学生体会随机性、频率的稳定性？初、高中两个学段的侧重点和发展点是什么呢？综合上述分析和思考，中学阶段“用频率估计概率”活动设计中，既要考虑学科性，又要兼顾两个学段的衔接发展问题. 从这两点出发，我们尝试给出两个学段活动的改进设计，并分析如何能够实现其教学目标.

2　频率稳定性的学科解释

大量关于随机事件的观察和实践表明[1]，随机事件有偶然性的一面，也有必然性的一面. 必然性表现为在大量重复试验中随机事件出现的频率的稳定性，即一个随机事件出现的频率常在某个固定的常数附近摆动，频率的稳定性说明随机事件发生的可能性大小是随机事件本身固有的、不随人的意志改变的一种客观属性，可以对其进行度量. 当进行大量重复试验时，可以用频率作为该随机事件概率的近似值，经常称之为概率的统计定义. 这里的频率稳定性是直观的说法，其严格的数学定义是用大数定律[2]来描述的：

设μn是n重贝努里试验*一般的，如果随机试验只有两个结果A和非A，把这个试验重复进行n次构成一个试验，称做n重贝努里试验.中事件A出现的次数，又A在每次试验中出现的概率为p(00，有

这里体现了偶然性和必然性的统一：必然性或稳定性是通过极限进行刻画的，与数学的极限不同，极限的对象是事件的概率序列. 而如(**)式则表达的则是数学的极限：即随着试验次数的增加，频率的极限为概率p，显然是不对的. 事实上即使试验次数非常大，频率值仍然有可能和p相差很大.

3　用频率估计概率改进活动设计*为了更直观说明，活动设计中使用了随机模拟的数据.

义务教育阶段[3]要求“知道通过大量重复试验，可以用频率估计概率”，高中阶段要求[4]“结合实例，会用频率估计概率；加深对随机现象的认识和理解. ”基于课程标准的要求及教学实践中出现的问题，我们给出中学阶段用频率估计概率两个核心点的改进活动设计：一是试验随机性，二是大量重复试验下频率的稳定性，活动设计既体现频率稳定性的学科理解，又考虑两个学段的衔接.

3.1　试验随机性活动设计

(1)试验随机性初中活动设计

以抛掷一枚质地均匀的硬币为载体，进行改进活动的设计.

在平整桌面上，全班分成10组进行抛掷硬币试验：尽量保持相同条件抛掷一枚硬币10次，并记录下“正面向上”的次数与频率；将全班所有组的结果进行汇总，填入表1.

表1

问题1比较10个小组得到的“正面向上”试验结果，你能发现什么？

问题2试验次数增加，结果会怎么样呢？

活动分析问题1通过比较10个小组的试验结果，体会相同条件下做同一随机试验，每组结果不一定相同；试验结果不一定等于理论值0.5，只有三个组正面向上的频率等于0.5；尽管10个小组得到的结果可能不同，但能从中发现一些规律，如所有频率都围绕0.5上下波动. 问题2在继续做试验之前提出猜想“随着试验次数的增加，频率会更加接近理论值0.5”，这也正是上文中提到的数学化的理解，事实上这只是一个随机事件，带着猜想进入下一步的试验进行检验.

(2)试验随机性高中活动设计

高中阶段建议使用信息技术进行模拟实验，我们使用Excel进行抛掷硬币模拟试验：抛掷一枚硬币40次，记录下“正面向上”的次数与频率；重复进行30组(表2)，并用散点图直观呈现(图1).

表2

图1

问题1比较30组“正面向上”试验结果，你能发现什么？

问题2根据这30组试验结果判断“正面向上”的概率是否为0.5？

活动分析问题1通过比较30组的试验结果，体会相同条件下做随机试验，每组结果不一定相同；30组正面向上频率只有4组恰好等于0.5，也有可能和0.5相差很远，如第29次为0.28；尽管30组得到的结果可能不同，但能从中发现一些规律：所有频率都围绕0.5上下波动，很多频率值和理论值0.5很接近. 问题2从数据推断的角度提出问题，以多个角度对这组数据进行分析并做出判断，初步体会并不一定频率正好等于0.5才能给出“正面向上”的概率是0.5，丰富对试验随机性的认识.

3.2　频率稳定性活动设计

(1)频率稳定性初中活动设计

分10组做40次掷硬币的试验，并将试验前10次、前20次、前30次、总40次的数据记录在表3.

表3

整理每个小组的试验结果，并将试验数据汇总填入表4—7：

表4

表5

表6

表7

为了更直观观察，将表4—7的数据用散点图表示(图2—5).

图2

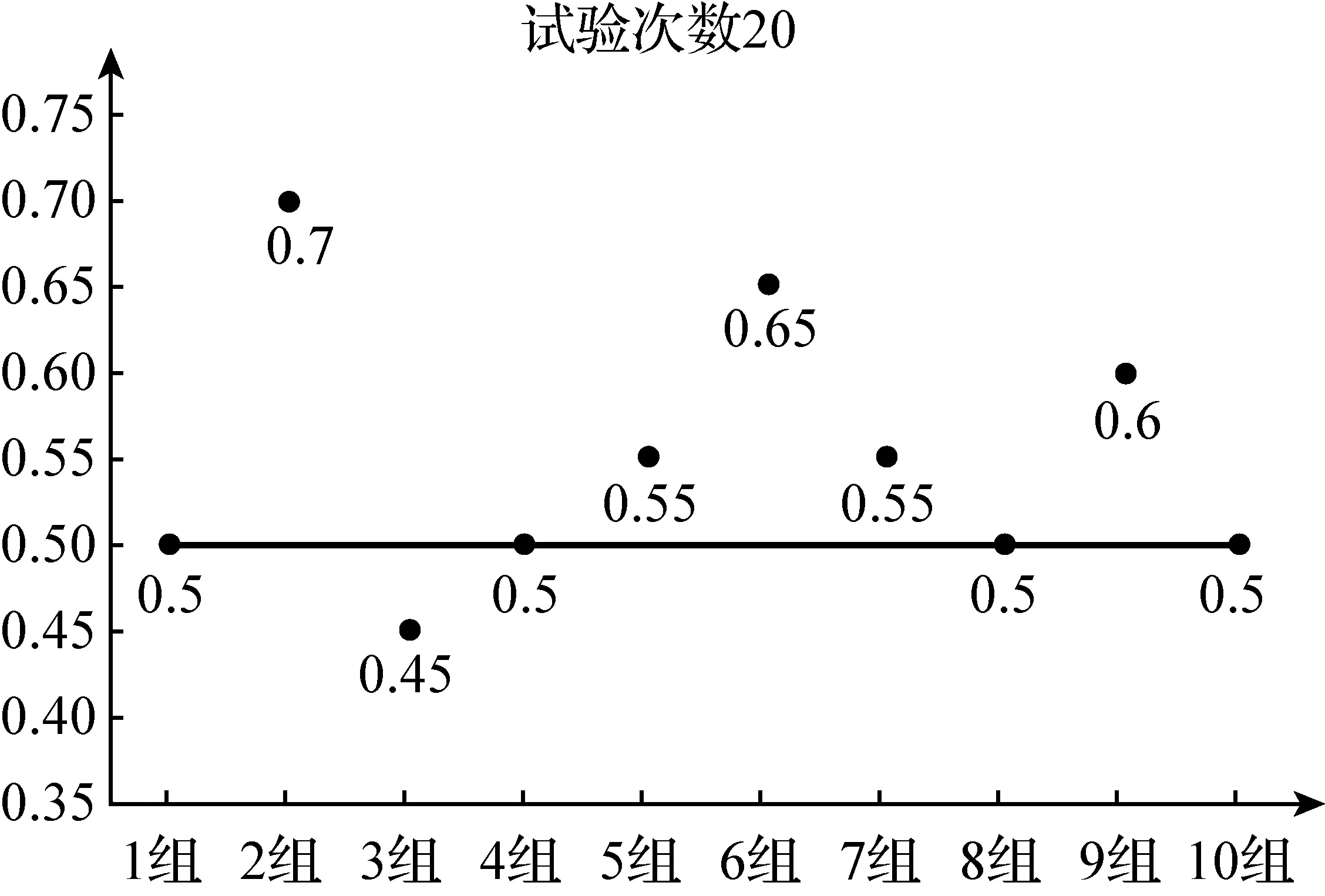
图3

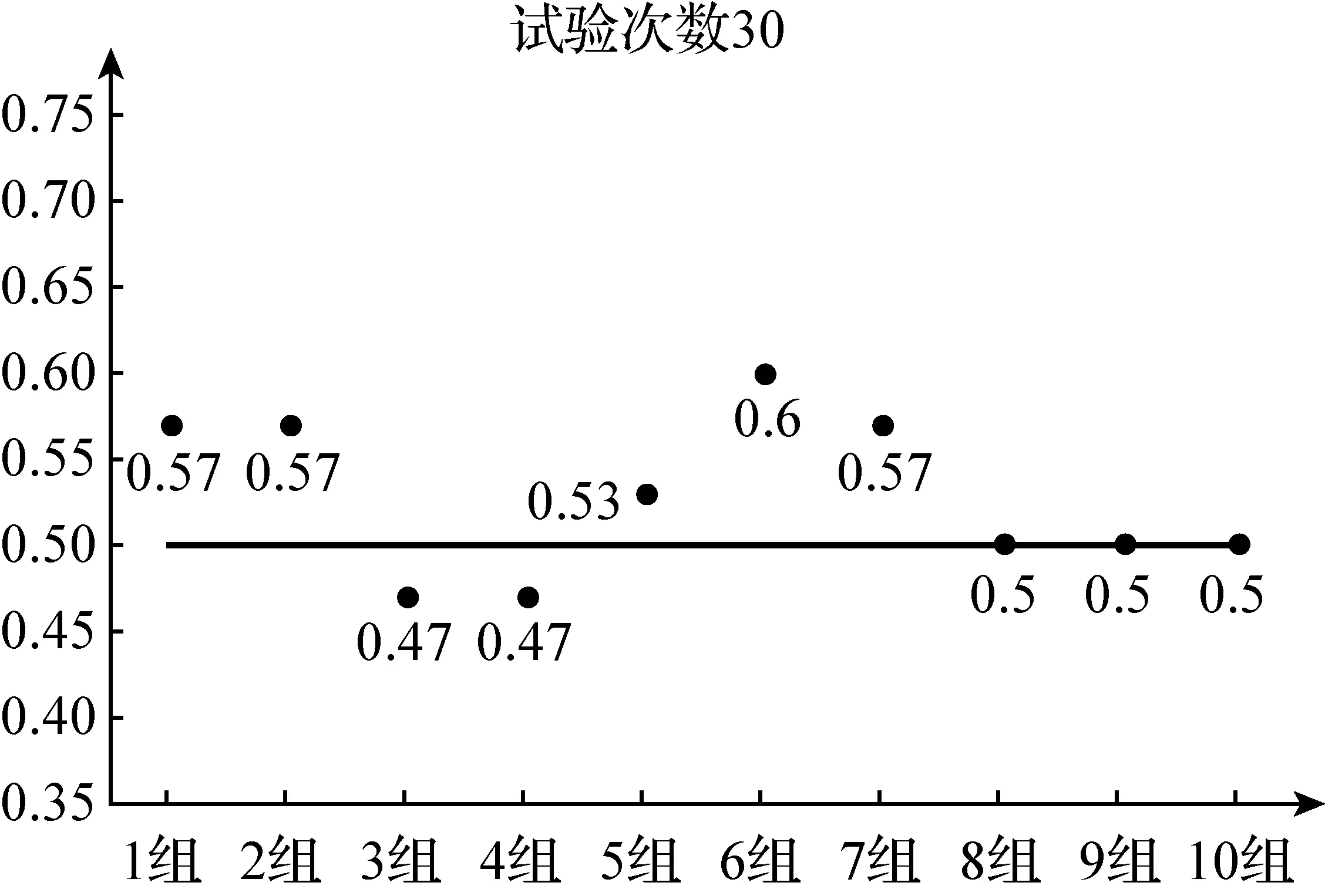
图4

图5

问题1在同一小组的试验中，观察 “正面向上”的频率(表3)随试验次数增加有何变化？

问题2观察不同小组在相同试验次数下

“正面向上”的频率(表4-7)，你有哪些发现？

问题3在图2-5中，观察不同试验次数下 “正面向上”频率的波动性，你有哪些发现？

活动分析问题1指向频率不确定性及稳定性初步体会：认识到随着试验次数增加，频率不一定更接近于理论值0.5，如第1组四个结果：0.7、0.5、0.57、0.58，初步体会频率与概率的区别；问题2进一步体会试验的随机性，依次观察四个不同试验次数下10组结果，试验次数相同时正面向上的频率不一定相同；问题3体会频率稳定性：将不同试验次数下“频率的波动性”作为观察对象，分别观察试验次数为10、20、30和40的频率波动大小(图2-5)：随着试验次数的增加，直观感受频率的波动性越来越小.进一步从定量角度刻画频率的波动性，可计算四个不同实验次数下10组结果与理论值0.5的平均绝对距离进行比较，分别为0.09、0.06、0.036、0.049，由直观感受到量化分析.

活动设计与给出一列增加的试验次数下频率规律变化是不同的，以上述数据为例，将所有组40次试验次数的结果累计并用折线图表示出来. 一列增加的试验次数下频率的变化趋势，即使教师在教学过程中并没有使用语言“一定”、“必然”等，给学生的直观印象仍然是随着试验次数增加，频率稳定于概率是必然的(表8、图6).

表8

图6

(2)频率稳定性高中活动设计

高中阶段频率稳定性的体会，我们设计了两个层次的活动：活动1是将“40次抛硬币”的组数增加，初步体会将“40次抛硬币”作为研究对象，当组数增多时更有“规律”；活动2是延续初中随机试验，从研究工具进行发展，特别是使用分布直方图进行数据分析.

活动1观察多组随机试验的频率稳定性

问题1根据这30组试验结果得到的频率，硬币正面向上、背面向上的可能性一样大吗？

问题2如果再增加组数，随机试验频率结果会有什么变化和规律？

活动分析高中阶段将在初中阶段基础上，将同一随机试验下随机事件发生的频率作为观测数据，并通过统计分析发现频率的取值规律，这是一个重要的发展点．高中生已经掌握了平均数、中位数、众数和方差等统计量，并可以用频率分布直方图表示数据，所以可以利用这些知识对同一随机试验下随机事件发生的频率进行分析，这是研究工具的发展. 问题1可以利用多种统计方法分析数据，体会频率的特征：比如这组数据平均数为0.49、中位数为0.515等、从频率分布直方图*直方图分组以0.5为中心，这里选择了0.06作为组距．(图7)可以看到大部分数据集中在[0.47,0.53)、数据分布不太对称等.问题2在更多组数据下，体会“频率”分布的相对稳定性，这里给出60组随机试验次数为40的频率分布直方图(图8)，比较图7和图8发现：试验组增多时数据分布更加对称，更多数据集中在理论值0.5附近.

图7

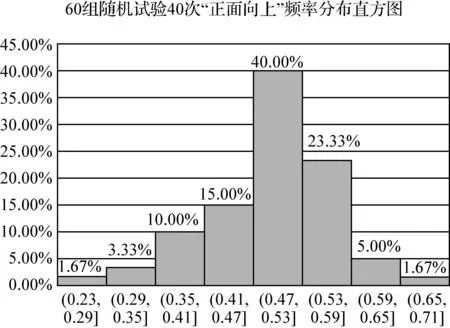
图8

活动2观察不同试验次数下频率的稳定性

问题组数不变，试验次数增加，分析频率的取值规律，你有哪些发现？

活动分析初中阶段主要通过直观方式初步认识频率的稳定性，高中阶段将在此基础上，应用初中学习过的数据整理和分析的方法进一步从定量、数据分布角度理解频率的稳定性，特别是从频率分布角度整体分析数据. 问题1是在活动1分析“同一随机试验下随机事件发生的频率”这组数据的基础上比较不同试验次数的两组数据，可以从集中趋势、离散程度等角度定量比较两组频率数据的稳定性；也利用直方图整体认识稳定性，在此基础上让学生体会统计推断的可靠性.这里给出30组试验次数为60的频率分布直方图(图9)，为方便比较，与图7纵坐标、分组情况是一致的.可以看出随着试验次数的增加，分布更加对称和集中，偏离0.5的值较少；以(0.5-0.09，0.5+0.09)为标准，试验次数为40和60落入该区间的比例分别为76.67%、93.33%，可以看出当试验次数为60时落在该区间的比例明显大于试验次数为40的，然而，落入区间(0.5-0.03，0.5+0.03)的比例则分别有43.33%、36.67%，试验次数为40次时落入这个区间的比例反而更大，原因是这是一次样本的结果，具有偶然性，教学中建议多进行几次试验，观察其规律．这样就将频率稳定性由初中的直观认识过渡到定量刻画,在此基础

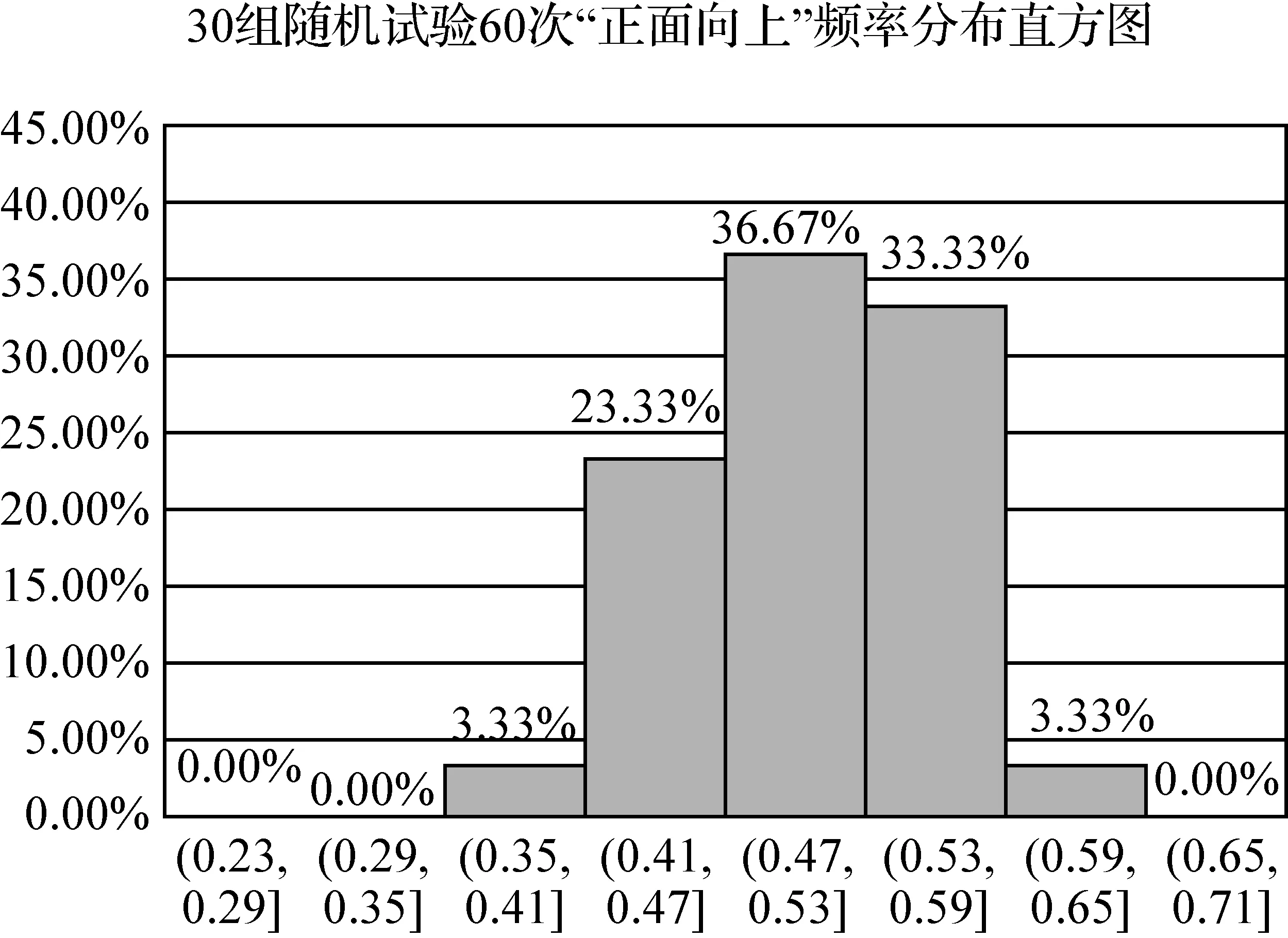
图9

上理解大量重复试验下频率估计概率的合理性与可靠性.

4　小结及进一步思考

用频率估计概率是中学统计与概率重要内容之一，很多一线教师对初中、高中两个阶段该内容的衔接和发展并不清楚，仅通过一列随着试验次数增加感受频率稳定性的活动设计不利于培养学生的统计思维.

我们从统计数据分析角度解释了大量重复试验下频率稳定性的含义，并对初中、高中频率与概率关系的关键活动进行了系列设计，核心观点一是体会试验结果的随机性，通过比较相同试验次数下的重复试验结果体会随机性；核心观点二是通过活动让学生理解频率的稳定性，进而理解用频率估计概率的合理性和可靠性；核心观点三是高中阶段的关键发展是研究工具的发展，特别是使用频率分布直方图进行分析，由初中阶段直观感受频率稳定性到高中阶段从定量角度刻画，进而理解大量重复试验下频率估计概率的合理性与可靠性.

进一步，除了内容理解、研究工具之外，根据学生发展水平，我们建议在高中阶段让学生参与到问题提出、试验活动方案设计、提出猜想、验证的全过程. 本文所给出的活动设计能否克服学生对频率稳定性的数学化、确定性理解，初中、高中阶段定位及衔接是否合理，高中阶段学生能否实现对研究对象的多角度认识等，都需要进行学生研究和教学实践的检验.