第二十一届北京高中数学知识应用竞赛决赛试题及参考解答

2018年3月25日

一、大学生张某，出行喜欢用共享单车，日常情况是周一到周五，每天要从宿舍到教学楼，骑行两个往返，每个单程用时10分钟；周末和国假回家(连续假日时，只需往返一次)，从宿舍到家单程骑行要50分钟．有A、B、C、D四家共享单车公司，其收费规则如下：

公司计费付费优惠A0.5元/次没有B1元/次周末和国假骑行免费C1元/次每月可以抽到一张奖券,用此券免费不计次连续骑行一周D1元/次每骑行付费一次,下次骑行免费

其中，使用半小时为一次；使用不足半小时，按一次计费.

如果不考虑押金和服务等因素，仅从用车付费的角度，且只使用一个公司的单车，你认为张某在这个学期(2月26日到7月13日)日常情况下，用哪个公司的共享单车最划算？说明理由.

解这个学期有20周，19个周末(含三天国假清明、五一，端午)，不足半小时的次数有(20×5-3)×4=388个，还有19×2=38个50分钟(回家、返校)的单程．对此，

若用A公司的车，约需付费：

388×0.5+38×1=232(元)；

若用B公司的车，约需付费：

388×1=388 (元)；

若用C公司的车，大体认为在4.5个月的周期里，可以免单4.5周，计费的学习日不超过15.5×5≈78天，周末加国假不超过15个，约为需付费不超过：78×4+15×4=372(元)；

若用D公司的车，约需付费：

综上所述，选用D公司的车最省钱，也就是最划算.另外，如此高频地用自行车，建议购置一辆普通自行车可以进一步降低骑行成本.

二、马尔萨斯是十八世纪知名的人口学家，1798年在论文《关于人口学原理》( Essay on the Principle of Population)中阐述了这样的观点：“如果一个国家的人口以几何级数无限制地增长，很快就会有几百万人因缺乏食物而无法生活”．文中又说：“假设人口数每25年翻一番，而且农产品在第一个25年翻倍，随后就以算术级数连续增加．经过一百年，人口数就会增加到11200万．但是生活保障条件仅仅能够维持3500万人的生活，这时将有7700万人完全没有生活来源．这是一个非常令人震惊的局面”.

对于“人口数每25年翻一番”这个假设，四十七年后，比利时学者威尔霍斯特于1845年使用美国1790年至1840年这五十年的人口普查数据(见表1)进行了验证.后来美国数学家佩尔等人于1920年又继续给出了其后从1850年至1910年这六十年的人口普查数据(见表2)．

表1　美国1790年至1840年的人口普查数据

表2　美国1850年至1910年的人口普查数据

请你根据这两个表，用简单的计算检验一下这120年间，马尔萨斯关于人口数25年翻一倍的假设是否正确.

解数据全部是每隔十年有一个观测值，要验证25年人口数是否翻一倍，就需要有间隔为五年的数据．为此我们在每相邻的两个观测值之间插入这两个观测值的平均数作为这个期间第五年的人口数，于是就得到下表所列的数据．表中第三列给出了各年在25年后人口数的增长率，如表中第三列中的第一个数1.15就是从1790年到1815年人口数的增长率，1.15 = 8438982÷3929827-1．由此可见，在1875年之前美国人口的25年增长率在1.05左右，可以认为每25年翻一倍．马尔萨斯的假设是成立的．但是在1875年以后随着人口数的增长，人口数的增长率在不断地降低，到1900年以后人口的25年增长率已经低于0.7，马尔萨斯关于25年人口翻倍的假设就不再成立了.

三、现有一种报警器，经测试，当灾难来临时它报警的概率是0.9999,当没有发生灾难时它不报警的概率是0.998.

使用这种报警器，可能会产生两种错误：一是因灾难来临时它没有报警，导致发生了灾难没有抢救，二是因没有发生灾难它报警，导致无谓地采取了抢救措施．这两种错误都会造成损失．不难看出，若只有一个报警器，发生这两种错误的概率分别是0.0001和0.002.

由于无法改善报警器的质量，为了降低这两种错误发生的概率，人们试图采取安装多个报警器的办法.

(1)如果安装两个报警器，可以有两种抢救方案：一种是只要有报警器报警就采取抢救措施；另一种是只有当两个报警器同时报警时，才采取抢救措施．请说明，无论哪一种方案都无法同时降低两种错误发生的概率.

(2)如果安装三个报警器，能否设计一种方案，使得两种错误发生的概率都会降低．如果能，请给出具体的设计；如果不能，请说明道理.

解(1)对于方案1，只要有报警器报警就采取抢救措施．即只有两个报警器都不报警，才不会去抢救.

当灾难发生时，两个报警器都不报警的概率是0.00012<0.0001．也就是说，发生灾难不能及时抢救的概率降低了，比原来只有一个报警器时要好.

当灾难不发生时，两个报警器都不报警的概率是0.9982，则此时至少有一个报警器报警的概率是1-0.9982>1-0.998=0.002，因此，此时去抢救的概率大于0.002．也就是说，不发生灾难时，却出去抢救的概率增大了，不如原来只有一个报警器时好.

对于方案2，只有当两个报警器同时报警时才采取抢救措施.

当灾难发生时，两个报警器都报警的概率是0.99992<0.9999．也就是说，发生灾难去抢救的概率降低了，不如原来只有一个报警器时好.

当灾难不发生时，两个报警器都报警的概率0.0022<0.002．也就是说，不发生灾难而去抢救的概率，比原来只有一个报警器时低了.

(2)分别讨论不同的方案.

第一个方案：3个报警器都报警才采取抢救措施.

此时，当灾难发生时，3个报警器都报警的概率是0.99993<0.9999．即发生灾难去抢救的概率不如一个报警器时好.

第二个方案：3个报警器中，只要有一个报警器报警就采取抢救措施.

此时，当灾难不发生时，只有在3个报警器都不报警时，才不会去抢救．由于3个报警器都不报警的概率是0.9983，因此，灾难不发生而去抢救的概率是1-0.9983>1-0.998=0.002，不如一个报警器时好.

第三个方案：3个报警器中，不止一个报警器报警时才采取抢救措施.

当灾难发生时，如果3个报警器都不报警或其中只有一个报警时，才不会采取抢救措施．这些事件发生的概率是0.00013+3×0.9999×0.00012<0.0001．换句话说，灾难发生时，没采取抢救措施的概率比原来只有一个报警器的情况要小.

当灾难不发生时，不止一个报警器报警，会采取抢救措施．这些事件发生的概率是0.0023+3×0.998×0.0022<0.002．换句话说，当灾难不发生时，采取抢救措施的概率比原来只有一个报警器的情况要小.

这表明，采取第三个方案会比只用一个报警器要好.

四、我国北方的很多城市街道交织成格，行人和车辆沿网格线行走，城市街道的抽象涵义是直角坐标系内平行于两条数轴的条条直线．于是，我们定义城市内街道上两点P(x1,y1)、Q(x2,y2)之间的距离为dPQ=|x2-x1|+|y2-y1|．并称之为曼哈顿距离(简称为曼距)．dPQ是P、Q之间所有连线(网格线)长度的最小值.

在城市里有一个地区，其中的相邻道路恰可近似地用过直角坐标系内格点(坐标为整数的点)的平行线表示，如图1.

图1

(1)求到点O(0, 0)的曼距为5的点构成的图形.

(2)该地区内有两个火警高危点A(-3, -2)和B(2, 2)，为了这两处的安全，预在某个格点位置设立一个消防站(格点位置四通八达)，问：这个消防站设在哪儿好？

解(1)设点P(x,y)满足dPO=|x-0|+|y-0|=5，由于城市道路上的点P(x,y)中的x和y至少一个是整数，所以当|x|+|y|=5时，x和y均是整数，即P(x,y)为格点．穷举可得P点的集合为{(0, -5)，(1, -4)，(2, -3)，(3, -2)，(4, -1)，(5, 0)，(4, 1)，(3, 2)，(2, 3)，(1, 4)，(0, 5)，(-1, 4)，(-2, 3)，(-3, 2)，(-4, 1)，(-5, 0)，(-4, -1)，(-3, -2)，(-2, -3)，(-1, -4)) }，对应的图形是顶点为(0, -5)、(5, 0)、(0, 5)、(-5, 0)的正方形上的所有格点.

(2)按照常识，消防队离火警高危地点越近越好，但一个消防站要兼顾A、B两点，可以认为好的消防站位置是指：消防站到A、B两点的曼距之和最小，在此基础上，消防站与A、B两点的曼距之差尽量地小.

由曼距的定义，A(-3, -2)和B(2, 2)两点之间的曼距

dAB=|2-(-3)|+|2-(-2)|=9，

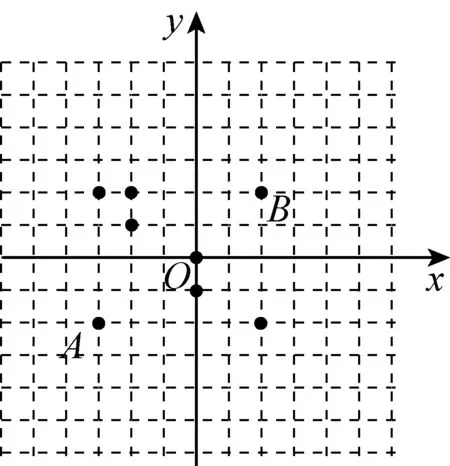
图2

将消防站的位置记作M，于是dMA+dMB≥9．以A、B为对角的矩形上及矩形内的任意格点为M，都有dMA+dMB=9，如图2．这个矩形外的任一格点P都是dPA+dPB>9.

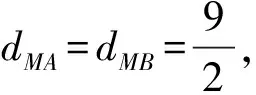
基于消防站与A、B两点的曼距之差尽量地小，于是在以A、B为对角的矩形上及矩形内考虑|dMA-dMB|=1，得到满足要求的点是(-3, 2)，(-2, 1)，(-1, 0)，(0, -1)，(1, -2)，(-2, 2)，(-1, 1)，(0, 0)，(1, -1)，(2, -2)，这10个位置可以作为消防站的选址.

五、根据中国汽车保值率研究委员会发布的《2017中国汽车保值率报告》，紧凑型SUV保值率排行榜如下表：

车龄排名1年2年3年4年5年品牌保值率品牌保值率品牌保值率品牌保值率品牌保值率第1名途观76.98%途观69.94%途观63.80%途观59.29%途观54.08%第2名奇骏75.16%奇骏69.41%CR-V思威63.28%丰田RAV458.01%奇骏52.17%第3名丰田RAV474.98%CR-V思威68.99%野帝62.48%奇骏57.58%CR-V思威50.56%第4名CR-V思威74.93%途胜68.05%奇骏62.36%CR-V思威57.01%丰田RAV450.45%第5名奥迪Q373.99%丰田RAV467.54%丰田RAV462.14%途胜56.39%翼虎49.35%第6名途胜73.95%现代ix3567.48%途胜62.14%翼虎55.13%奥迪Q348.98%第7名现代ix3573.82%野帝67.27%翼虎61.27%奥迪Q354.76%域胜00748.33%第8名翼虎73.56%翼虎67.21%现代ix3560.30%野帝54.75%途胜48.24%第9名野帝73.48%奥迪Q367.15%域胜00760.02%域胜00754.29%宝马X146.84%第10名狮跑73.24%狮跑65.91%奥迪Q359.77%北京4054.12%奔腾X80 46.61%

汽车保值率是指某款车型在使用一段时期后，将其卖出的价格与先前购买价格的比值.由表可见，汽车保值率排名是随车龄的变化而变化的．一般来讲，保值率是购车者的一项参考指标．请你综合上表数据，给出适当假设、排名原则和计算方法，为购车人列出仅考虑保值率指标下的前5名汽车品牌.

解1．假设

(1)购车人大概在购车后的5至10年间将这辆车再卖掉；

(2)上表呈现的品牌汽车保值率的变化规律均在五年后适用.

2．排名原则

(1)在上表中，从未出现在前5名的品牌不在考虑之列；

(2)虽然每辆车的保值率逐年下降，但保值率的变化幅度是不同的，在原则(1)的前提下，保值率整体变化幅度小的品牌汽车排在前面.

3．具体排名计算如下

1°按照排名原则(1)，参加排名的汽车是：途观、奇骏、丰田、CR-V思威、奥迪Q3、途胜、翼虎、野帝，共8种品牌车.

2°计算上述8种品牌汽车中每种车5年内保值率的整体变化幅度．具体算法是：

先计算出汽车每年保值率的下降值，再计算出每一年比上一年汽车保值率降幅的变化(即保值率下降值的差，称为降幅)，最后求5年的降幅之和．这个和就是5年内保值率的整体变化幅度.

由于野帝汽车在第5年已经不在前十名，没有数据，设其第5年的保值率为46.5%(稍小于第10名).

上述每一步的计算结果用下表列出．

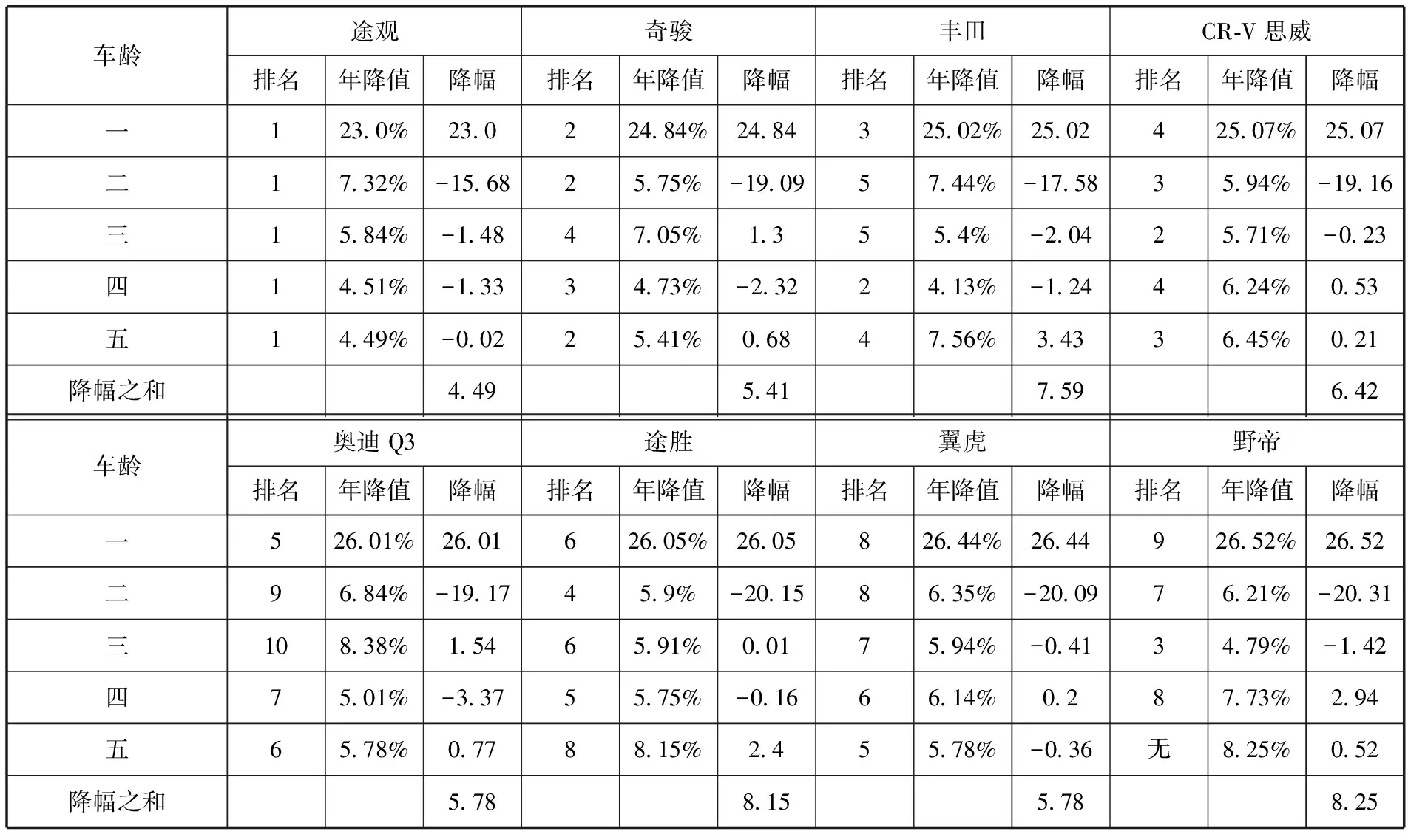
车龄途观奇骏丰田CR-V思威排名年降值降幅排名年降值降幅排名年降值降幅排名年降值降幅一123.0%23.0224.84%24.84325.02%25.02425.07%25.07二17.32%-15.6825.75%-19.0957.44%-17.5835.94%-19.16三15.84%-1.4847.05%1.355.4%-2.0425.71%-0.23四14.51%-1.3334.73%-2.3224.13%-1.2446.24%0.53五14.49%-0.0225.41%0.6847.56%3.4336.45%0.21降幅之和4.495.417.596.42车龄奥迪Q3途胜翼虎野帝排名年降值降幅排名年降值降幅排名年降值降幅排名年降值降幅一526.01%26.01626.05%26.05826.44%26.44926.52%26.52二96.84%-19.1745.9%-20.1586.35%-20.0976.21%-20.31三108.38%1.5465.91%0.0175.94%-0.4134.79%-1.42四75.01%-3.3755.75%-0.1666.14%0.287.73%2.94五65.78%0.7788.15%2.455.78%-0.36无8.25%0.52降幅之和5.788.155.788.25

3° 根据假设(2)，将每种品牌车在5年内保值率的整体变化幅度当作购车后的5至10年间该车的保值率的整体变化幅度．于是得到汽车保值率名次由1至5的顺序是：途观、奇骏、奥迪Q3、翼虎、CR-V思威．