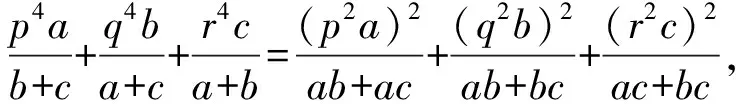对数学问题2121的探究

李凤清　张子卫　张青山

(四川职业技术学院应用数学与经济系　629000)

数学问题2121在锐角三角形ABC中，求证：

设三角形ABC的面积为S，由于

我们由这个式子的结构联想到著名的几何不等式——佩多不等式.

佩多不等式对任意两个三角形A1B1C1与三角形A2B2C2，|B1C1|=a1,|A1C1|=b1,|A1B1|=c1，|B2C2|=a2,|A2C2|=b2,|A2B2|=c2，记三角形A1B1C1的面积为S1，三角形A2B2C2的面积为S2，那么

(1)

仅当三角形A1B1C1与三角形A2B2C2相似时等号成立.

(2)

由此可见，问题2121可以推广成下面命题.

pcotA+qcotB+rcotC≥4S

(3)

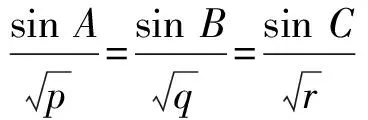
显然，等号成立的条件也可以表示为

cotA:cotB:cotC

=(q+r-p):(p+r-q):(p+q-r).

定理1显然与佩多不等式等价.因此，问题2121是佩多不等式的一个特例.

由(3)式可知

(pcotA+qcotB+rcotC)2≥16S2，

由于

cotAcotB+cotBcotC+cotCcotB=1，

那么可得

(pcotA+qcotB+rcotC)2

≥16S2(cotAcotB+cotBcotC+cotCcotA)，

令a=cotA,b=cotB,c=cotC，

就有(pa+qb+rc)2≥16S2(ab+bc+ca)，

我们提出下面问题.

(pa+qb+rc)2≥16S2(ab+bc+ca)

(4)

是否恒成立？

分析

1. 若ab+bc+ca≤0，(4)式显然成立；

2.若ab+bc+ca>0，由于(4)式是一个三元二次齐次不等式，故可设ab+bc+ca=1.

第一种情况，a,b,c中至少有两个正数，不妨设为a,b，则存在三角形ABC使

a=cotA,b=cotB,c=cotC(注：设两个锐角A,B满足a=cotA,b=cotB，那么

=cot [π-(A+B)]，

令C=π-(A+B)，

可见0

由定理1可知(4)式成立；

第二种情况，a,b,c全为负数，则存在三角形ABC使|a|=cotA,|b|=cotB,|c|=cotC，

由定理1可知(4)式成立；

第三种情况，a,b,c中有两个负数，一个正数，不妨设a<0,b<0,c>0，那么

(pa+qb+rc)2≥16S2(ab+bc+ca)

结合互联网大数据种类多、系统庞大和信息量大等特点建设共享时代的智慧城市，发展可持续增长经济。纵观世界格局发展趋势，世界多级化明显。全球经济命运共同体的提出，为智慧城市大数据中心的建设铺平了道路。智慧城市大数据中心的建设需要以互联网技术为基础，以大数据技术为载体，建立全球范围内的经济贸易联系系统。智慧城市大数据中心的基础就是互联网技术[3]。智慧城市的建设与发展要在中国特色社会主义城市建设与发展的引导下，改革创新，因地制宜，努力探索出符合我国国情的现代化城市建设方针政策，各级政府部门也要积极配合智慧城市的建设工作，调动优势资源，充分发挥大数据中心数据收集平台的消息传递快和信息量大的优势。

等价于

(p|a|+q|b|-rc)2

≥16S2[|a||b|+|b|(-c)+(-c)|a|]，

故存在三角形ABC使

|a|=cotA,|b|=cotB,-c=cotC，

由定理1可知(4)式成立.故以下命题成立.

证明由于

(qbcos 2R+rccos 2Q+pa)2+(qbsin 2R-rcsin 2Q)2

≥0，

那么

(pa)2+(qb)2+(rc)2+2(pa)(qb)cos 2R+

2(pa)(rc)cos 2Q+2(qb)(rc)(cos 2Rcos 2Q-

sin 2Rsin 2Q)≥0,

即

(pa)2+(qb)2+(rc)2+2(pa)(qb)cos 2R+

2(pa)(rc)cos 2Q+2(qb)(rc)cos (2R+2Q)≥0,

即

(pa)2+(qb)2+(rc)2+2(pa)(qb)cos 2R+

2(pa)(rc)cos 2Q+2(qb)(rc)cos 2P≥0,

即

(pa+qb+rc)2-4(pa)(qb)sin2R-

4(pa)(rc)sin2Q-4(qb)(rc)sin2P≥0,

即得

(pa+qb+rc)2≥16S2(ab+bc+ca).

易知等号成立的条件为

pa∶qb∶rc=sin 2P∶sin 2Q∶sin 2R，

即

a∶b∶c=(q+r-p)∶(p+r-q)∶(p+q-r).

对三角形ABC，|CA|=b,|CB|=a,|AB|=c，不妨设A,B为锐角，那么

pcotA+qcotB+rcotC

在定理2中令a=cotA,b=cotB,c=cotC，即可得到(3)式，即是说，由定理2可以得到定理1，说明定理1与定理2等价.

根据定理2即可将数学通报数学问题1885推广为下面结论：

若三角形PQR的三边长度分别为p,q,r，其面积为S，a,b,c为正数，则

由定理2即可得证.