无位置传感器永磁无刷直流电动机换相校正技术

孙 灿，施晓青

(南京航空航天大学，南京 211100)

0 引 言

近年来，永磁无刷直流电动机因其功率密度高、控制简单和体积质量小等良好的性能发展迅速。由于永磁无刷直流电动机在高速运行下转子位置检测困难，无位置传感器控制已成为高速电机领域一个重要研究方向，现已研究出多种控制技术。它们大多是利用检测定子电压、电流等容易获取的物理量进行转子位置的估算以获取位置信号，其中主要有反电动势法、三次谐波电势法、电感法、状态观测器法等。反电动势法是目前应用最多的方法，它一般指通过检测电机反电动势来获得转子位置信号的方法。由于在任意时刻总有一相绕组是不导通的，这时候绕组的端电压从绕组端部到直流地之间或相电压从绕组端部到中心点之间就反映出该相绕组的感应电势[1]。

现有的包括反电动势法在内的各种无位置传感器控制算法往往存在转子位置检测误差，从而引起换相误差。例如，反电动势法中使用滤波电路，使获取到的相电压过零点通常与实际相电压的过零点之间存在相位误差，而造成电机换相点偏移引起换相误差。此外，由于电机存在绕组感抗，换相时相电流不能突变，使得电流上升和下降都需要一定的时间，导致相电流滞后于相反电动势。所以，永磁无刷直流电动机在传统无位置传感器控制策略下并非位于最佳换相点，导致电机转矩/电流比降低，影响电机的性能。

对此，国内外也做了相应研究。文献[2]通过各种实验，证明了对永磁无刷直流电动机换相点的校正能有效抑制电流相位滞后，提高电机系统性能。文献[3]证明了使电机换相点提前能有效抑制电流相位滞后导致的输出转矩随速度升高而下降的现象，并且最佳换相点会随速度变化。文献[4]证明了永磁无刷直流电动机提前换相点可以减小电机的损耗。文献[5]证明了换相点能的提前可减小转矩的波动，并提高转速的输出。文献[6]证明了提前电机换相点也能有效改善低转矩脉动无刷直流电动机的性能。文献[7]研究发现，永磁无刷直流电动机在合理的换相点换相能提高电机系统的性能。

换相点校正技术的关键是选取最佳超前换相角，来合理补偿电流的相位滞后角。目前,换相点校正的方法主要有以下3种。一是直接固定超前换相补偿角。如文献[8]提到的，以永磁无刷直流电动机的效率、转矩脉动和转速范围作为性能指标，在0～16°电角度范围内提前电机的换相点进行实验，观察不同换相点对电机性能的影响。该方法只能用于电机恒速运行的情况，且实际运行中难以选取合适的补偿角度。二是基于数学模型求取补偿角的解析公式。文献[8]提出换相点的最佳提前角度应为换相过程所转过角度的一半，但未给出理论依据和超前角的求取方法。三是结合无位置传感器控制算法。主要是利用三次谐波反电动势或三次谐波转子磁链与PLL锁相环的结合。如文献[9]实现了基于转子磁链三次谐波的无位置传感器的换相点校正控制。但该方法只适用于电机磁链和反电动势包含大量三次谐波且波形远偏移正弦波分布的情况，并且为了提高控制精度，通常会对其采用低通滤波处理，导致相位延迟，需要额外的相位补偿措施。除上述方法以外，文献[10]利用BP神经网络实现了使电机在全转速范围内在最佳换相点进行换相，但该方法控制复杂。所以，探究一种不依赖于电机参数、控制精度高、控制简单，且适用范围广的换相点校正方法十分有必要。本文针对永磁无刷直流电动机在高速运行下转子位置检测困难的问题，在传统反电动势法的基础上，探究了一种基于坐标变换的无位置传感器控制策略[11]；然后，针对永磁无刷直流电动机固有的电机相电流滞后问题，在坐标变换法无位置传感器控制驱动策略下,探究了一种基于转子磁链观测的最大转矩/电流比换相校正控制算法(以下简称MTPA)[12]。为最终实现高速下的无位置传感器控制及MTPA控制奠定了基础。

1 基于坐标变换的无位置控制策略

1.1 传统反电动势法的原理

由于反电动势过零点滞后30°电角度处即为电机的换相点，所以在永磁无刷直流电动机无位置传感器技术中反电动势常被作为研究对象[13]。因反电动势无法被直接检测，通常通过检测电机相电压或端电压的过零点来表示反电动势过零点。图1即为传统的相电压法检测电路，通过分压滤波电阻网络能得到包含反电动势过零点信息的相电压信号。图1中，Ua为A相绕组端电压；Re为电机的等效内阻；Le为每相绕组的等效电感；ea，eb，ec为相反电动势。

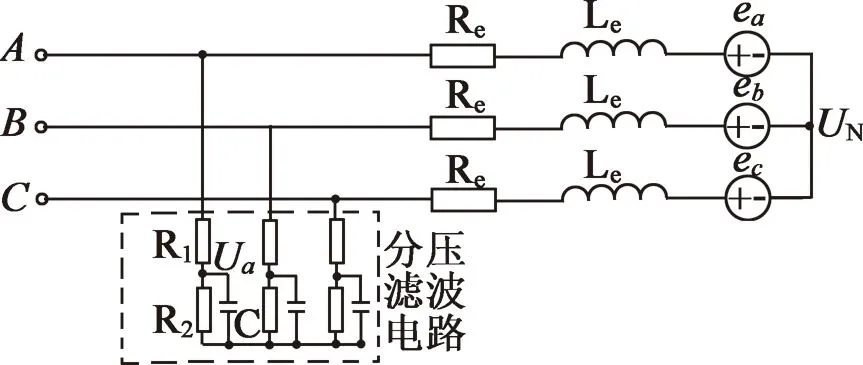
图1 相电压检测电路

在这种方法中，R1，R2和C构成的滤波电路可消除脉冲宽度调制时高频斩波以及二极管续流等因素对电压信号造成的干扰，但同时会引起相移[12]，导致最终获取到的相电压过零点通常与实际相电压的过零点之间存在相位误差。

由滤波电路的相频特性可求得相移角α：

(1)

由式(1)可见，该相移角依赖于电机转速以及滤波电路的参数值。通常情况下，将滤波电路的截止频率设计为能使额定转速下的相移角正好为30°电角度。但这种将滤波滞后角度固定为额定转速下30°电角度的控制方法，存在一定缺陷。当电机转速变化时，滤波后相电压的过零点与实际相电压的过零点之间的相位误差也会变化，即α未被消除。所以，需要探究一种新的无位置传感器控制算法。

1.2 坐标变换法无位置传感器控制算法

针对反电动势法中电机转速等参数影响滤波电路相频特性的问题，本文研究了一种基于坐标变换理论的无位置传感器控制方法。该方法在反电动势信号的基础上通过坐标变换构造出能直接用于电机换相控制的信号，该信号与滤波后的相电压之间存在相位差，且可控，通过控制这个相位差可以将滤波后相电压信号的过零点直接控制在需要的电机换相点，从而补偿了转子位置信号误差。 下面将具体介绍这种坐标变换法的原理。

如图2所示，定义a,b,c坐标系和A,B,C坐标系分别各有3个互差120°电角度的坐标轴，并定义A,B,C坐标系超前a,b,c坐标系β电角度。设Ua，Ub,Uc分别为滤波后的三相相电压，其基波方向分别为a,b,c坐标系中3个坐标轴的方向。该方法通过对原始a,b,c坐标系变换到A,B,C坐标系的方法直接提取换相点，即在反电动势信号的基础上通过坐标变换构造出能直接用于电机换相控制的信号。

图2 坐标变换示意图

对Ua，Ub,Uc分别进行傅里叶级数分解，如下式:

(2)

式中:Ud为母线电压；n=1,3,5，…；an和bn为与转速有关的系数；ω为电角速度。

将a,b,c坐标系中的Ua，Ub和Uc投影到A,B,C坐标系中，得UA，UB和UC：

(3)

UA,UB和UC的基波方向分别为A,B,C坐标系中3个坐标轴的方向。

以A相为例，结合式(2)和式(3)可得式(4)：

令n=0，n=1，n=3m(m=1,3,5,…) ,以及n=5对UA进行各次谐波分析，分别得UA的直流分量、基波、3m次谐波以及5次谐波的表达式：

(5)

由式(5)可见，经坐标变换得到的UA的直流分量和3m次谐波分量为零，5次及5次以上谐波含量很低，可忽略，所以可用UA的基波近似代替UA本身，则UA与Ua基波间的相位差就是A,B,C坐标系与a,b,c坐标系间的相位差β角，即可把A,B,C坐标系与a,b,c坐标系间相位差角β角作为相电压滤波后的信号Ua的过零点与换相点间的相位差α角的补偿角，通过控制β=α，就可以实时地将坐标变换得到的UA信号的过零点控制在所需要的换相点。对于B相和C相，结论相同。

但是在该方法中，换相点补偿角β的求取过分依赖于电机参数以及分压滤波电路的参数值，因此得到的变换角度不精确。而且，该方法未考虑相电流在换相时不能突变，相电流滞后于相反电动势的问题，导致永磁无刷直流电动机在该控制策略下并非位于最佳换相点，电机转矩/电流比降低，影响了电机的性能。

2 基于转子磁链观测的换相点校正技术

针对永磁无刷直流电动机高速运行时，基于坐标变换法的无位置控制策略中变换角度不精确、相电流滞后相反电动势的问题，本文研究提出将换相点校正技术应用到基于坐标变换法的无位置传感器控制策略中，来抑制这种电流相位滞后，以实现MTPA控制。

2.1 磁链法换相点校正技术原理

换相点校正技术的关键是使相电流与对应的相反电动势同相位，所以本文所探究的换相点校正方法以检测反电动势基波相位和相电流基波相位得到它们的相位差为出发点，以换相点前移补偿相位差为目标，形成对相位差的闭环控制，达到通过换相点校正来提高电机性能的效果。

永磁无刷直流电动机的反电动势信号无法直接被检测，所以利用转子磁链信号代替反电动势信号做相位检测处理，推出转子磁链的表达式：

(6)

式(6)中:ψa为转子磁链;ua和ia分别为电机相电压和相电流;Le为绕组的等效电感。

由式(6)可知，将位置传感器检测到的电机相电压和相电流进行相应计算，就可以得到转子磁链信号。由于转子磁链是相反电动势的积分，应与反电动势滞后90°电角度后同相位，所以将电流也做积分变换，得到同样滞后90°电角度的信号 ：

(7)

反电动势、转子磁链和相电流以及积分后的电流信号相位关系如图3所示，经过积分变换后的相电流信号滞后于转子磁链信号的相位角，应与相电流信号滞后于反电动势信号的相位角一致。图3中，α′为相电流信号滞后于反电动势信号的相位角。

图3 反电动势、转子磁链和相电流以及积分后的电流信号相位关系图

考虑到信号中直流分量的干扰，在磁链观测环节和电流积分环节之前先对检测到的相电压与相电流进行相同程度的高通滤波处理来滤除直流分量；然后将转子磁链波形与积分后的电流信号通过相同的低通滤波，以提高波形正弦度。最后得到的两正弦波之间的相位差仍与相电流信号滞后于反电动势信号的相位角α′一致。通过PI调节，就可得到与α′相等的补偿角β′。

2.2 坐标变换无位置控制法与换相点校正的结合

坐标变换法的关键是对补偿角β的控制， 而本文所探究的换相点校正法的关键是换相点补偿角β′的获得，所以将坐标变换法与换相点校正法相结合就可以实现高速永磁无刷直流电动机在无位置传感器下的MTPA控制。

由于本文所探究的换相点校正方法能实时地检测反电动势与相电流的相位差角即最佳换相点与现换相点间的相位差角α′，并对该相位差做闭环调节最终得到稳定的补偿角β′，不依赖于电机转速以及分压滤波电路的参数值，所以能弥补坐标变换无位置方法中变换角度不精确的问题，并实现该驱动系统下的换相点校正，使电机在无位置传感器控制下保持在最佳换相点运行。具有换相点校正环节的坐标变换法无位置传感器永磁无刷直流电动机的驱动系统如图4所示。

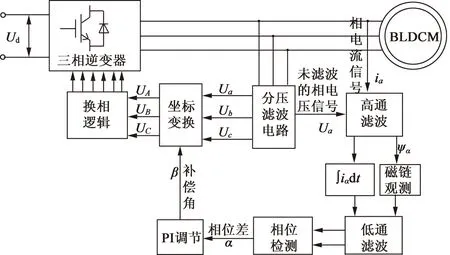
图4 坐标变换与换相点校正相结合的驱动系统

3 仿真验证

为了验证本文所探究的换相点校正方法对于改善高速永磁无刷直流电动机基于坐标变换法的无位置传感器控制的有效性和优越性，使用MATLAB/Simulink平台对该方法进行了仿真验证，本文实验样机参数如表1所示。

表1 仿真电机的主要参数

首先，固定换相补偿角，使不带换相点校正环节的无位置传感器无刷直流电动机控制系统模型在额定转速(n=50 000 r/min)下运行，对0～30°电角度范围内不同变换角下的换相进行仿真测试，对应转矩/电流比值的仿真结果如图5所示(这里的转矩Te与电流i之比表示单位电流下电机出力大小，单位为N·m/A)。

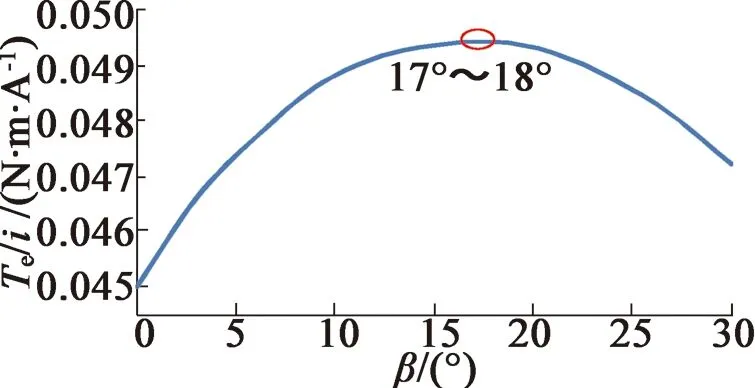
图5 不同变换角下的转矩/电流比

然后，在额定转速n=50 000 r/min的运行状态下，对未加换相校正的无位置传感器电机控制系统模型进行仿真测试，如图6所示。由图6(a)可知，相电流明显滞后于反电动势；由图6(b)可知，滤波后的转子磁链信号和电流积分信号，比之于反电动势和相电流分别滞后了同样的角度，即前两者间的相位差即是反电动势与相电流间的相位差。所以，可用滤波后的转子磁链与电流积分间的相位差代替反电动势与相电流间的相位差进行换相点校正控制，符合理论分析。

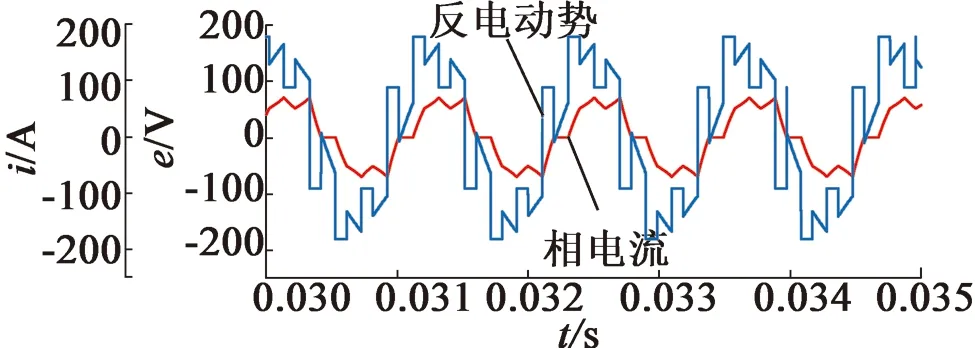
(a) 反电动势和相电流之间的相位关系

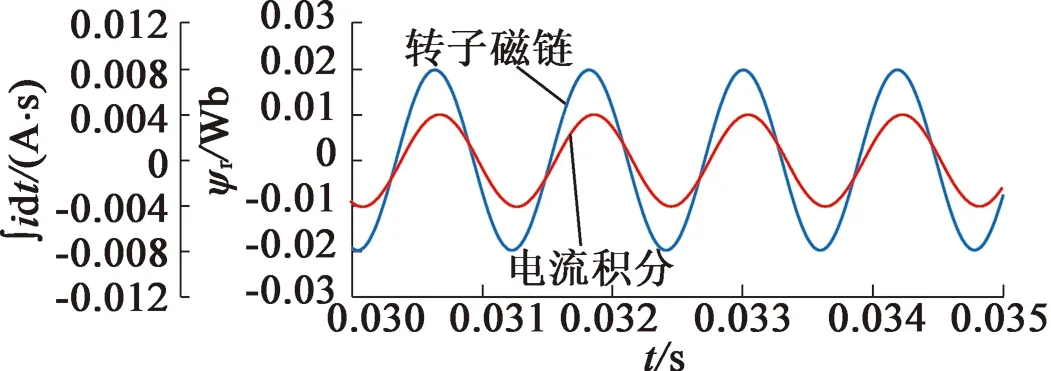
(b) 滤波后转子磁链和电流积分的相位关系

接着，对含换相点校正环节的无位置传感器电机控制系统模型在额定转速n=50 000 r/min的运行状态下进行仿真测试，如图7所示。由图7可见，电机的电流积分信号波形和转子磁链信号波形中心重合，即反电动势与相电流的相位关系一致。即证明了所探究的换相点校正方法对解决相电流相位滞后问题有显著的效果。

图7 含换相点校正的相位关系

由换相点校正原理及过程分析可知，换相点校正环节中PI调节器的输出值即为坐标变换环节的变换角值，如图8所示。由图8仿真结果可知，换相点校正环节实时检测的相位差经PI调节后，换相角逐渐趋于稳定，直至相位差降为零。

图8 换相点校正控制下PI输出值

可见，本文所探究的换相点校正方法能对电机的运行状态有效地进行换相校正，提高电机的性能，验证了高速永磁无刷直流电动机坐标变换法无位置传感器控制策略和磁链法最大转矩/电流比换相校正算法的有效性及优越性。

4 结 语

1) 探究了基于坐标变换的高速永磁无刷直流电动机无位置传感器控制算法，并借助MATLAB/Simulink仿真平台搭建了电机驱动控制模型，实现了电机在坐标变换法下的无位置传感器控制。

2) 搭建的换相点校正环节与坐标变换法相结合的永磁无刷直流电动机无位置传感器控制模型，验证了换相点校正环节对改善坐标变换法无位置传感器控制性能的有效性和优越性。

[1] 李和明.无刷直流电动机无位置传感器控制的研究[D].杭州:浙江大学,2007:1-14.

[2] SPEE R,WALLACE A K.Performance characteristics of brushless DC drives [J].IEEE Transactions on Industry Applications,1988,24(4):568-573.

[3] SAFI S K.Analysis and simulation of the high-speed torque performance of brushless DC motor drives [J].IEE Proceedings - Electric Power Applications,1995,142(3):191-200.

[4] 赵宏涛,吴峻.定子磁链提前换相增加直线永磁无刷直流电动机的推力[J].中国电机工程学报,2011(3):118-123.

[5] CHAU K T,CUI W,JIANG J Z,et al.Design of permanent magnet brushless motors with asymmetric air gap for electric vehicles [J].Journal of Applied Physics,2006,99(8):1241.

[6] PARSA L,LEI H.Interior permanent magnet motors with reduced torque pulsation [J].IEEE Transactions on Industrial Electronics,2008,55(2):602-609.

[7] LEE D M,LEE W C.Analysis of relationship between abnormal current and position detection error in sensorless controller for interior permanent-magnet brushless DC motors[J].IEEE Transactions on Magnetics,2008,44(8):2074-2081.

[8] 罗宏浩,吴峻,赵宏涛,等.永磁无刷直流电动机换相控制研究[J].中国电机工程学报,2008,28(24):108-112.

[9] SHEN J X,IWASAKI S.Sensorless control of ultrahigh-speed PM brushless motor using PLL and third harmonic back EMF[J].IEEE Transactions on Industrial Electronics,2006,53(2):421-428.

[10] 程伟,徐国卿,冯江华,等.基于BP网络的电动汽车用无刷直流电动机转矩角控制技术研究[J].电工技术学报,2006,1(3):62-66.

[11] 吴元元,邓智泉,王晓琳,等.基于正交坐标变换的永磁无刷直流电动机转速估计方法[J].中国电机工程学报,2012,32(6):145-149.

[12] SHI X,WANG X,GU C,et al.A novel commutation cor-rection method for high-speed PM brushless dc motor[C]//Applied Power Electronics Conference and Exposition.IEEE,2017:1899-1905.

[13] CHENG K Y,LIN Y T,TSO C H,et al.Design of a sensor-less commutation IC for BLDC motors[C]//Power Electronics Specialists Conference.IEEE,2002:1365-1375.