槽口宽度和磁极偏心对伺服电动机齿槽转矩的影响

孙兆琼，李定华，钱荣超

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

近年来机器人产业飞速发展，越来越多的领域开始使用机器人代替人力，而伺服电动机作为执行单元，是机器人的核心部件，对机器人的工作性能有着重要影响[1]。伺服电动机运行时转矩脉动过大会导致机器人工作时产生抖动现象，从而影响机器人的定位精度，而齿槽转矩是定子铁心的齿槽与转子永磁体相互作用产生的磁阻转矩，是转矩脉动的重要组成部分。因此，降低齿槽转矩的角度对抑制转矩脉动具有十分重要的意义。

从电机本体设计的角度讲，通常削弱伺服电动机齿槽转矩的方法有：采用分数槽绕组；选取合理的极槽配合；齿顶开槽；缩小定子槽口宽度；采用不等气隙(转子磁极偏心)；采用定子斜槽、转子斜极的方法等[2-5]，但以往文献主要针对传统分布式绕组的电机进行齿槽转矩的研究，目前，公开发表的文献中对机器人用集中绕组拼块式定子铁心的伺服电动机齿槽转矩的研究还属空白。

本文以一台集中绕组拼块式铁心的永磁伺服电动机为例，采用傅里叶分解电机齿槽转矩的解析式，同时采用有限元分析方法，研究改变定子槽口宽度和磁极偏心，削弱齿槽转矩的影响。

1 原理分析

对于永磁电机来说，产生的转矩可按下式计算[6,7]：

(1)

展开可得：

(2)

当电机定子绕组不通电时，齿槽转矩可表示：

(3)

假设电枢铁心内的磁导率无穷大，不通电时，电机内存储的磁能可近似表示为永磁体和气隙中的磁能之和，即：

(4)

式中：θ为转子位置角；α为某一定子齿中心线与某一永磁体中心线之间的夹角。

气隙磁通密度沿电枢表面的分布可表示：

B(θ,α)=Br(θ)G(θ,α)

(5)

式中：Br(θ)为永磁体剩磁磁通密度;G(θ,α)为有效气隙长度沿气隙圆周的分布。

将式(3)用傅里叶级数展开可得齿槽转矩的解析表达式：

(6)

2 建立求解模型

2.1 电机结构

针对机器人的运行要求，其内部的伺服电动机应具备体积小质量轻的特点，因此通常将电机设计成集中式绕组拼块式定子铁心、表贴式磁钢的结构，如图1所示。这种结构可以大幅度地提高槽满率，减小端部绕组体积。电机的主要参数如表1所示。

图1 电机结构图

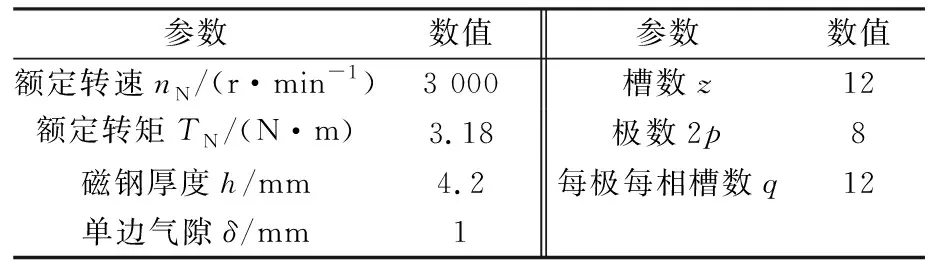
参数数值参数数值额定转速nN/(r·min-1)3 000槽数z12额定转矩TN/(N·m)3.18极数2p8磁钢厚度h/mm4.2每极每相槽数q12单边气隙δ/mm1

2.2 求解模型

本文研究的伺服电动机为对称结构。因此，沿圆周方向取1/4横截面建立求解模型，并进行网格划分，求解模型的剖分网格如图2所示。

图2 伺服电动机求解模型剖分图

本文采用参数化分析的方法分别对2个方案进行了有限元计算[7，8]。方案一：将磁极偏心ΔRmag设定为常数，将槽口宽度Bs0设定为在(0 ～2 mm)区间内的线性变量，分别计算不同槽口宽度对应的齿槽转矩Tcog；方案二：将槽口宽度Bs0设定为常数，将磁极偏心ΔRmag设定为在(0～15 mm)区间内的线性变量，分别计算不同转子偏心对应的齿槽转矩Tcog。伺服电动机的槽口宽度Bs0及转子偏心ΔRmag如图3所示。

图3 槽口宽度Bs0及转子偏心ΔRmag示意图

3 计算结果分析

3.1 改变槽口宽度对削弱齿槽转矩的影响

通过有限元分析计算了不同槽口宽度时的齿槽转矩，齿槽转矩随时间变化的曲线如图4所示。定子槽口宽度Bs0分别为0,0.4 mm,0.8 mm,1.2 mm,1.6 mm,2.0 mm时的齿槽转矩峰峰值Tcpp如表2所示。

图4 不同槽口宽度时的齿槽转矩曲线

参数数值槽口宽度Bs0/mm00.40.81.21.62.0齿槽转矩峰峰值Tcpp/(mN·m)19.312.67.613.83144.6

图5 齿槽转矩的傅里叶分布(Bs0=0.8 mm)

3.2 改变磁极偏心对齿槽转矩的影响

通过有限元分析计算了不同磁极偏心时的齿槽转矩，齿槽转矩随时间变化的曲线如图6所示。转子磁极偏心ΔRmag取值分别为0,3 mm,6 mm,9 mm,12 mm,15 mm时的齿槽转矩峰峰值Tcpp如表3所示。由图6中曲线和表3中计算数据对比可以看出，随着磁极偏心的增加，齿槽转矩的峰峰值先减小后增加，在ΔRmag=12 mm时，齿槽转矩的峰峰值最小。当转子磁极偏心时，磁极中心线处的气隙较小，磁极两端的气隙较大，使电机的气隙磁通密度沿圆周方向上的分布接近正弦，即不等气隙，可通过参数化分析获得最优的磁极偏心数值。

图6 不同磁极偏心时的齿槽转矩曲线

参数数值磁极偏心ΔRmag/mm03691215齿槽转矩峰峰值Tcpp/(mN·m)33.826.721.212.66.726.9

图7 齿槽转矩的傅里叶分布(ΔRmag=12 mm)

4 结 语

通过本文的研究得出如下结论：

2)对于分数槽电机,并非定子槽口宽度越小越好，随着槽口宽度的减小，齿槽转矩的峰峰值先减小后增加，槽口宽度取值在接近零的一定范围内存在最优方案。

3)当转子磁极偏心时，电机为不等气隙结构，电机的气隙磁通密度沿圆周方向的分布接近正弦，通过参数化分析获得最优的磁极偏心数值，使对应的齿槽转矩最小化。

[1] 邓必懋,朱涛.浅析我国工业机器人技术的产业化发展[J]. 机械工程与自动化，2017,4(2):222-224.

[2] 唐旭，王秀和，田蒙蒙，等.基于改变定子齿槽参数的异步起动永磁同步电动机齿槽转矩削弱措施研究.[J]. 电工技术学报, 2016, 31(23):1-8.

[3] 王秀和，杨玉波，丁婷婷，等. 基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J]. 中国电机工程学报,2015,25(15):146-149.

[4] 李文军，杨惠忠. 闭口槽结构对永磁无刷电机齿槽转矩削弱研究[J]. 煤矿机械,2017,38(4):28-30.

[5] 王晓远, 贾旭. 基于槽口优化的电动汽车用大功率无刷直流电机齿槽转矩削弱方法[J].电工技术学报, 2013,25(6):40-45.

[6] 谭建成. 永磁无刷直流电机技术[M]. 北京:机械工业出版社, 2011:193-215.

[7] 孙兆琼，钱荣超，冷小强，等. 永磁同步电动机电枢反应电抗计算[J].微特电机，2013， 41(9):20-22.

[8] 吴苏敏. 基于Ansoft的永磁同步电机结构参数优化研究[D]. 成都：电子科技大学，2014. 15-29.

[9] 陈世坤.电机设计[M]. 北京:机械工业出版社, 2000:23-75.