永磁同步电动机的速度指定位置跟踪控制

王宝军，王家军

(浙江交通职业技术学院， 杭州 311112)

0 引 言

随着电机控制技术的发展，永磁同步电动机(以下简称PMSM)在当前的精确位置驱动领域起到了非常重要的作用。与直流电动机和感应电动机相比，PMSM具有结构紧凑、功率密度高、转矩惯量比大、转矩电流比高，以及控制性能更加突出等优点[1，2]。根据PMSM的不同应用场合，PMSM的应用主要用于位置控制、速度控制和转矩控制3个方面。PMSM位置控制的性能受到摩擦、参数变化、未知负载转矩和未建模动态等各种不确定因素的影响[3，4]。为了提高PMSM位置控制的性能，当前许多先进的控制技术被应用到PMSM位置控制的设计，例如滑模控制[5，6]、反推控制[7]、神经网络[8]和模糊控制[9]等。

一般情况下，PMSM的位置控制包括3个控制环，即位置环、速度环和电流环。根据当前的控制方法，PMSM的速度控制由位置环的输出进行控制，即PMSM的速度无法由外部进行调节。如果在PMSM位置控制过程中能够增加一个速度控制的自由度，这将有利于提升PMSM位置控制的精度和设计灵活性。因此，如何在PMSM位置控制的过程中增加一个速度控制的自由度是本文所要解决的关键问题。

跟踪控制问题是当前现代控制理论研究的一个重要方面。跟踪控制问题可以分为2大类：轨迹跟踪和路径跟踪[10]。轨迹跟踪就是使得系统的某个状态能够跟踪一个与时间相关的参考给定信号。与轨迹跟踪相对应，路径跟踪是使系统的某个状态跟踪一个不受时间、速度和加速度等约束的参考给定信号。轨迹跟踪问题可以看作是一个特殊的路径跟踪问题。当前在所有的PMSM位置跟踪问题中，给定参考信号包含了时间、速度和加速度等控制信息。因此，这类位置跟踪都可以归结为轨迹跟踪问题。如果在PMSM位置跟踪过程中能够指定电机速度的大小，这种控制方式对于PMSM的位置跟踪控制是非常有意义的。借助于参考文献[10]中的控制设计思路，PMSM的速度指定位置跟踪控制可以分为两步设计，第一是使位置跟踪一个设定的路径，第二是使位置的跟踪满足指定的速度指标。

反推控制是非线性反馈控制中的一种反向递推设计方法[11]。反推控制的最大优点是借助虚拟状态变量，采用一步一步的Lyapunov函数设计，使高阶非线性系统的控制设计变得非常简单。同时，反推控制的这种反向递推设计方法对于不确定参数的自适应估计也是非常有利的。反推控制已经广泛应用于PMSM的控制中。文献[12]将反推控制应用于PMSM的速度跟踪控制中。文献[13]基于输入-输出精确线性化，利用反推控制实现了PMSM对于未知参数和负载转矩干扰的鲁棒控制。

在PMSM位置跟踪控制的过程中，由于电机的转速相对来说比较低，这使得位置跟踪的性能受未知负载转矩的影响较大。如果在PMSM 位置跟踪的过程中能够提高未知负载转矩的估计速度，这将有利于进一步提高PMSM位置跟踪的精度。干扰观测器是解决运动控制系统中未知参数和负载干扰问题的有效手段[14]。当前干扰观测器的设计绝大部分都是在频域范围之内进行设计，系统的稳定性很难证明。本文给出了一种新颖的干扰观测器设计方法，这种干扰观测器可以独立于PMSM位置控制器，可以有效降低未知负载干扰对于位置控制精度的影响。

1 PMSM的模型

在转子d-q坐标系内，典型的表贴式PMSM的数学模型可以表示如下:

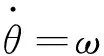
(1)

(2)

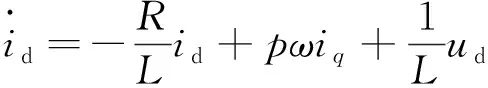
(3)

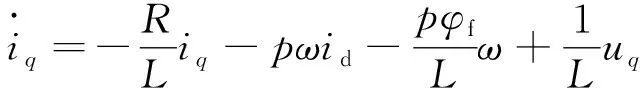
(4)

式中：θ为转子角度；ω为转子角速度；R为定子电阻；L为定子电感；id和iq为定子d和q轴电流；ud和uq为定子d轴和q轴电压；p为极对数；φf为转子永磁磁通；J为转子的转动惯量；B为粘滞摩擦系数；TL为负载转矩。

在磁场定向控制(或者矢量控制)中，直轴电流id常常设定为零，因此式(1)～式(4)中的PMSM模型可以简化如下:

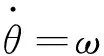
(5)

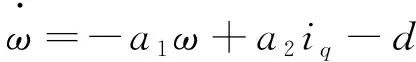
(6)

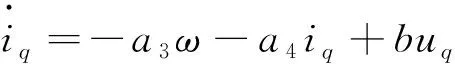
(7)

式中：a1=B/J，a2=kT/J，a3=pφf/L，a4=R/L，b=1/L，d=TL/J，kT=3pφf/2。

2 PMSM速度指定位置跟踪控制的设计

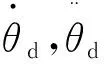
PMSM的位置信号θ和位置给定信号θd为时间的函数，它们分别为θ(t)和θd(t)的缩写。一般的位置跟踪控制可以称为基于时间指定的位置跟踪控制，即在某一指定时刻位置信号θ到达给定的位置θd。基于时间指定的位置跟踪可以表示:

(8)

式中：η(t)为位置跟踪误差。式(8)的物理意义代表PMSM的转子位置能够渐进跟踪给定位置信号。

与时间指定位置跟踪相对应，PMSM的速度指定位置跟踪是指在某个指定的位置，PMSM能够保持某个指定的速度。在一般位置跟踪控制设计中，给定位置设定为θd(t)的模式，即给定位置是时间的函数。如果给定位置设定为时间的间接函数，即给定位置设定为θd[γ(t)]，则通过这种方式可以在位置跟踪过程中增加一个速度指定控制自由度。速度指定可以采用下面的方程式实现[10]:

(9)

式中：η(t)为速度指定控制误差；vd[θd(t),t]为PMSM相应位置的指定速度控制变量。由式(9)可知:

(10)

为了有利于PMSM速度指定位置跟踪控制的设计，利用自适应反推控制设计方法可以较方便地将速度指定控制引入控制器设计。针对式(5)～式(7)，自适应反推控制设计可以分为三步。

第一步：选择PMSM的位置跟踪误差作为第一个虚拟状态变量:

x1=θ-θd(γ)

(11)

第一步的Lyapunov函数可以设计如下:

(12)

式(11)中虚拟状态变量x1的导数:

(13)

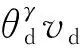
第二个虚拟状态变量x2选择:

(14)

式中：k1>0为正常数。利用式(13)和式(14)可得:

(15)

利用式(15)，则Lyapunov函数V1的导数:

(16)

第二步的Lyapunov函数V2设计如下:

(17)

Lyapunov函数V2的导数可以表示:

(18)

式(14)中虚拟状态变量x2的导数可以表示:

第三个状态变量x3选择:

利用式(19)和式(20)，Lyapunov函数V2的导数可以改写:

第三步的Lyapunov函数V3设计如下:

(22)

Lyapunov函数V3的导数可以表示:

由式(20)可知，虚拟状态变量x3的导数:

(24)

针对式(23)，如果设计控制器uq和相应的自适应控制环节如下：

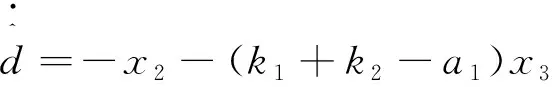
(26)

(27)

则可以保证:

(28)

由前面的控制设计过程可以得出，该自适应反推控制设计可以实现如下3个方面的功能：

(1) 位置的跟踪：θ→θd；

由前面的推导设计过程可以得出，自适应反推控制需要设计2个自适应律，这增加了系统设计复杂性，同时未知负载的估算受虚拟状态变量的影响。如果能够对于未知负载转矩的估计进行独立设计，这将有利于简化系统控制的设计，同时也可以提高未知负载转矩估算的精确性。

3 干扰观测器的设计

PMSM干扰观测器的系统设计如图1所示，主要包括控制器、干扰观测器和PMSM。根据文献[15]，对于式(5)～式(7)中的PMSM模型，干扰观测器可以设计为如下形式:

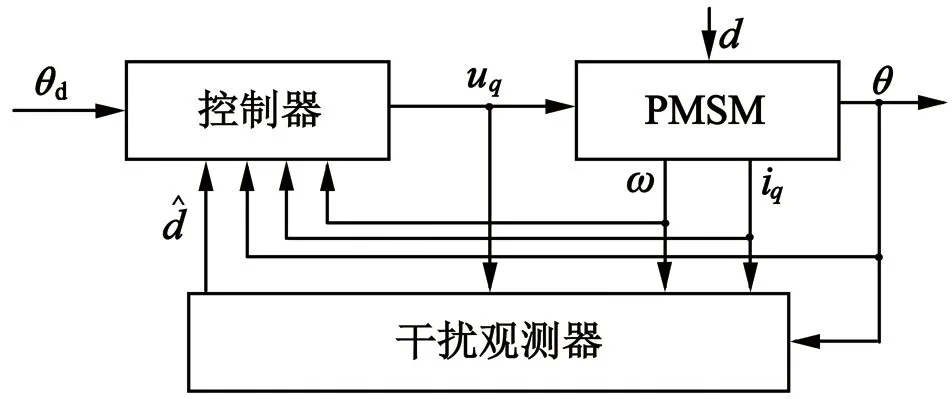
图1 具有干扰观测器的控制系统结构

(29)

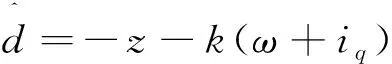
(30)

式中:k>0为正常数。

定理：针对式(5)～式(7)中的PMSM模型，在不考虑控制器设计的情况下，式(29)、式(30)可以实现PMSM未知项d的估计。

证明：利用式(5)～式(7)和式(29)、式(30)，PMSM未知项估计误差的导数可以表示:

式(31)可以简化:

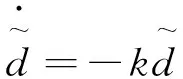
(32)

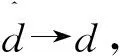
上述PMSM干扰观测器的设计具有如下3个方面的优势：

(1) 干扰观测器的设计简单，可以增强系统的抗干扰能力；

(2) 干扰观测器是指数稳定的，其设计不依赖系统控制器的设计；

(3) 干扰观测器是基于状态方程设计的，这使得其稳定性证明变得简单。

4 仿真分析

用于PMSM仿真模型的参数如表1所示。

表1 PMSM的模型参数

由表1可以获得式(5)～式(7)中的模型参数：a1=0.5，a2=4 900，a3=26.1，a4=80，b=40。

4.1 未知参数采用自适应估计方法的仿真

对于未知负载转矩采用自适应估计的PMSM速度指定位置跟踪的控制结构如图2所示。在系统控制器设计中有4个参数k1,k2,k3和k4需要进行调整，4个参数调整原则如下：

图2 采用自适应估计的PMSM控制系统结构

(1)将k3和k4设定为零，调整参数k1和k2，这种情况属于采用普通反推控制的位置跟踪；

(2)将k4都设定为零，保持将k1和k2不变，调整k3，这种情况属于具有未知负载自适应估计的位置跟踪；

(3)保持将k1,k2和k3不变，调整k4，这种情况属于具有速度指定的位置跟踪。

采用上述的参数调节方法,可以得到控制参数：k1=8，k2=250，k3=3 200，k4=20 000。

4.1.1 负载转矩为未知常数时的仿真

假定PMSM的负载转矩为1 N·m，相对于控制器设计来说是未知的。PMSM的给定位置为θd(γ)=sinγ，其中γ为时间的函数，γ的初始值设定为γ(0)=π/2，电机的初始值设定为θ(0)=0。

在第一种情况下，指定速度控制变量vd为vd=10 rad/s，仿真结果如图3所示。由仿真结果可以得出，稳态位置最大位置跟踪误差为0.010 5 rad，最大负载转矩估计误差为1.15 mN·m。在第二种情况下，降低指定速度控制变量vd为vd=5 rad/s，仿真结果如图4所示。由仿真结果可以得出，稳态位置最大位置跟踪误差为0.003 35 rad，最大负载转矩估计误差为0.54 mN·m。

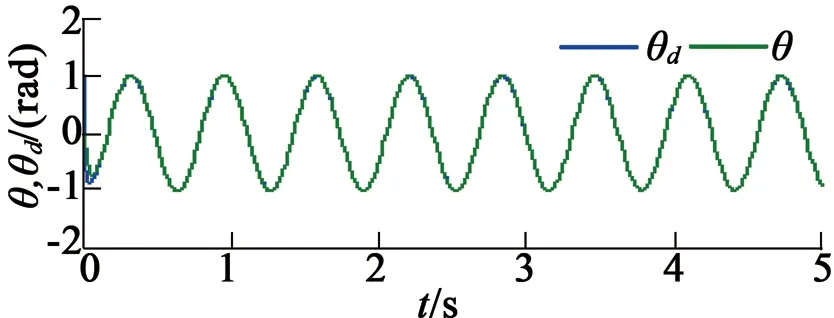
(a) 参考位置和实际位置

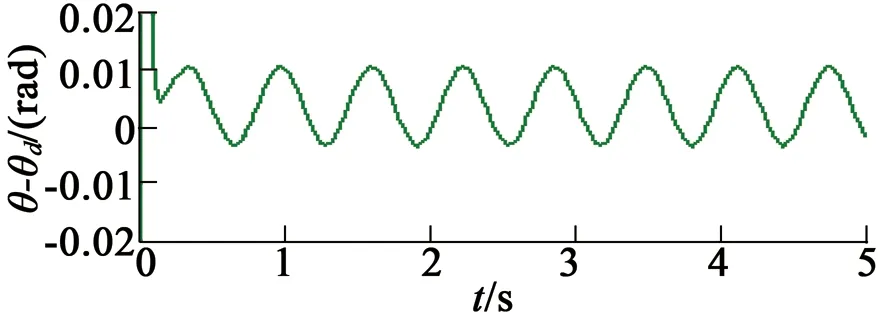
(b) 位置跟踪误差

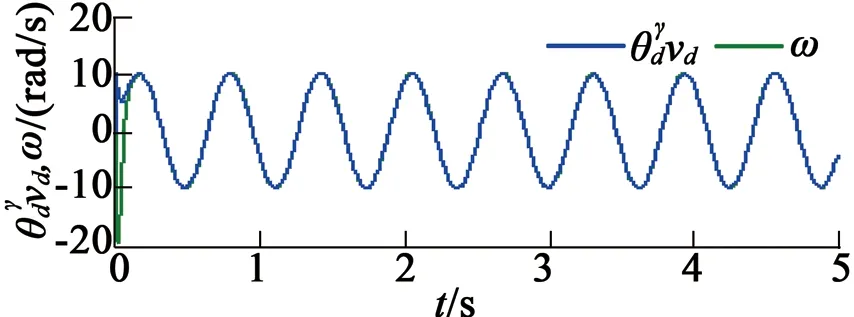
(c) 指定速度与实际速度

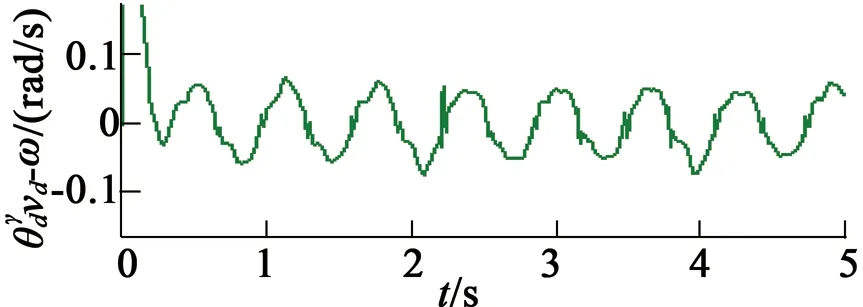
(d) 速度误差

(e) 负载转矩与估计转矩

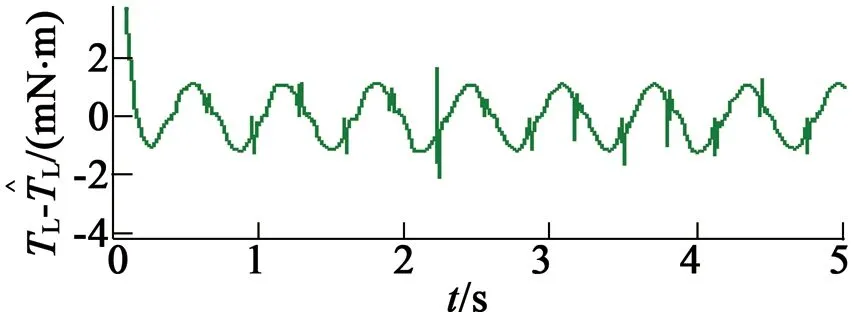
(f) 负载转矩估计误差

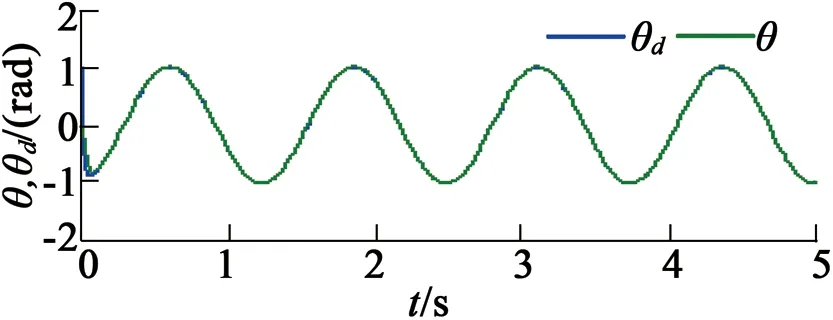
(a) 参考位置和实际位置

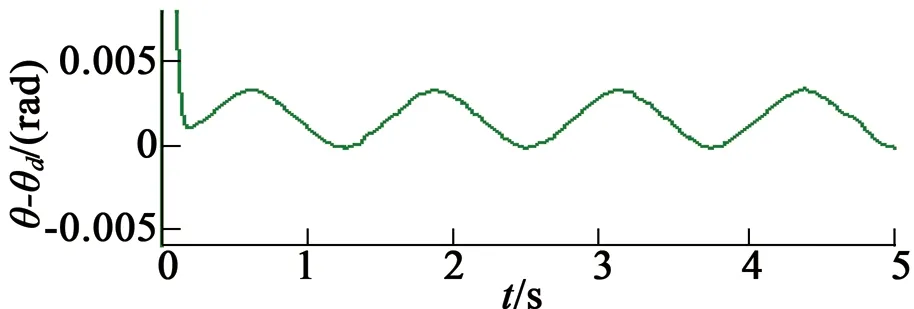
(b) 位置跟踪误差

(c) 指定速度与实际速度

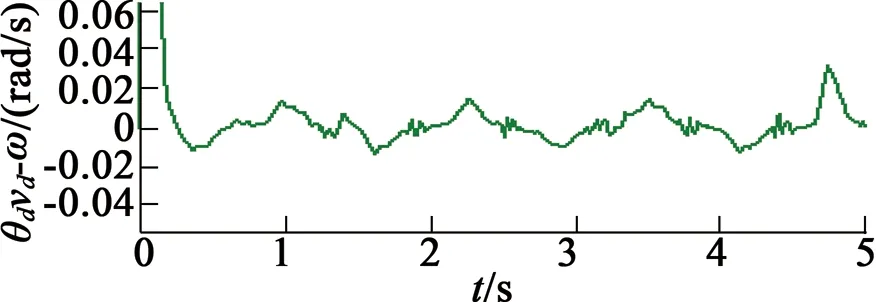
(d) 速度误差

(e) 负载转矩与估计转矩

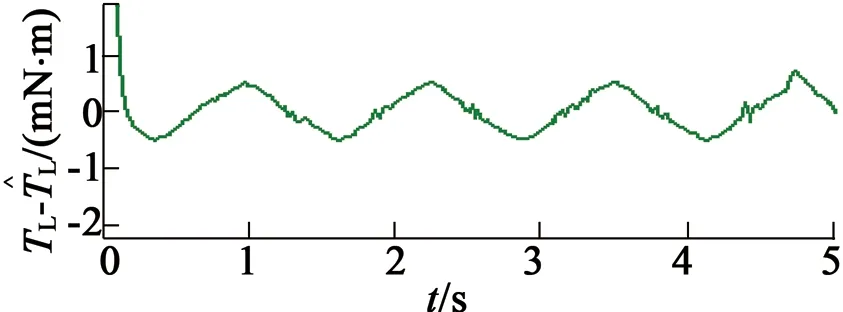
(f) 负载转矩估计误差

由第一种情况和第二种情况的仿真可以看出，PMSM的位置能够跟踪指定位置信号，通过改变指定速度控制变量vd可以调节位置跟踪的精度；同时自适应环节可以实现负载转矩的估计，降低负载转矩对于位置跟踪的影响。

4.1.2 负载转矩为未知变化量时的仿真

假定PMSM的负载转矩为1～2 N·m的随机变化转矩，初始条件与前面一致。

在第三种情况下，指定速度控制变量为vd=10sint，仿真结果如图5所示。在第四种情况下，降低指定速度控制变量为vd=5sint，仿真结果如图6所示。

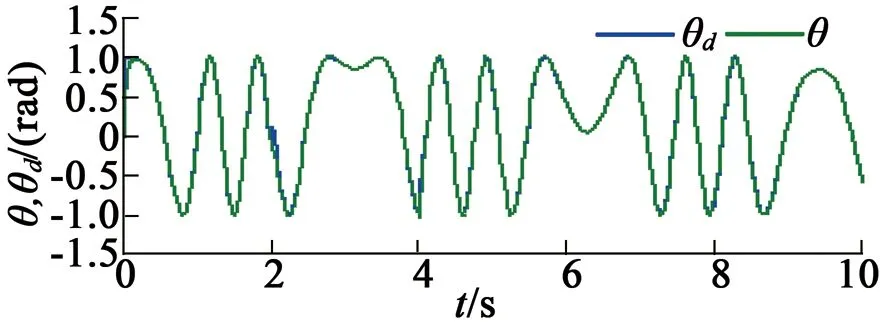
(a) 参考位置和实际位置

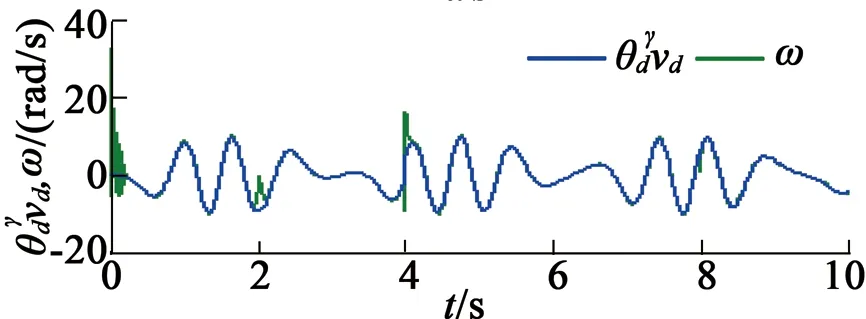
(c) 指定速度与实际速度

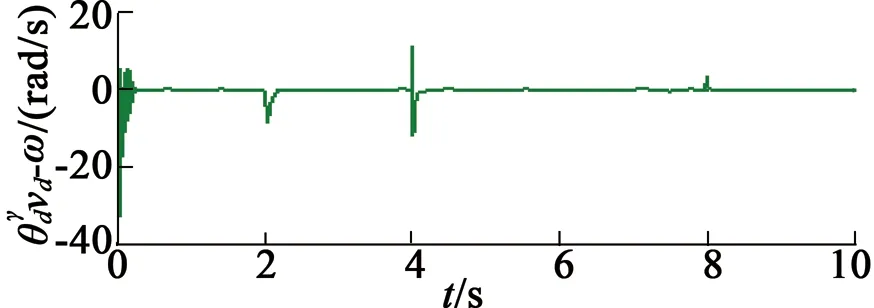
(d) 速度误差

(e) 负载转矩与估计转矩

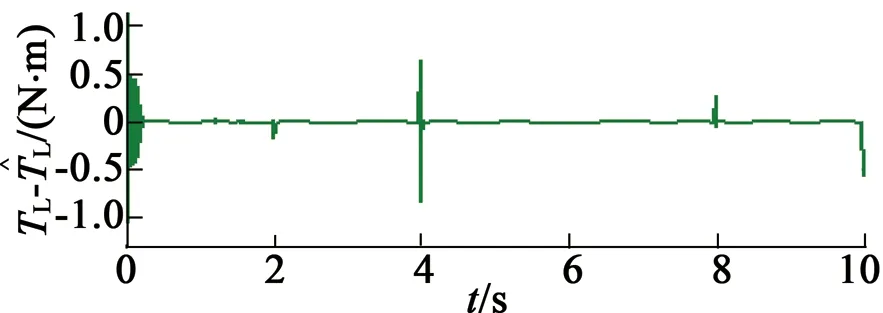
(f) 负载转矩估计误差

(a) 参考位置和实际位置

(b) 位置跟踪误差

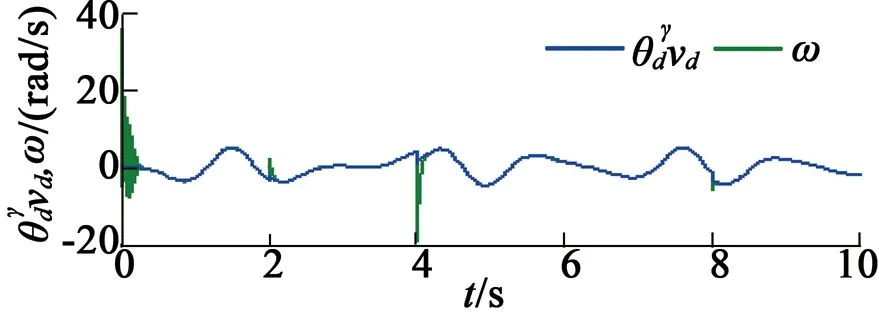
(c) 指定速度与实际速度

(d) 速度误差

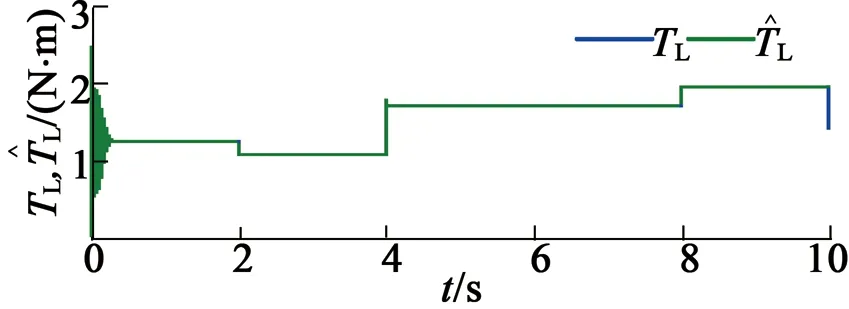
(e) 负载转矩与估计转矩

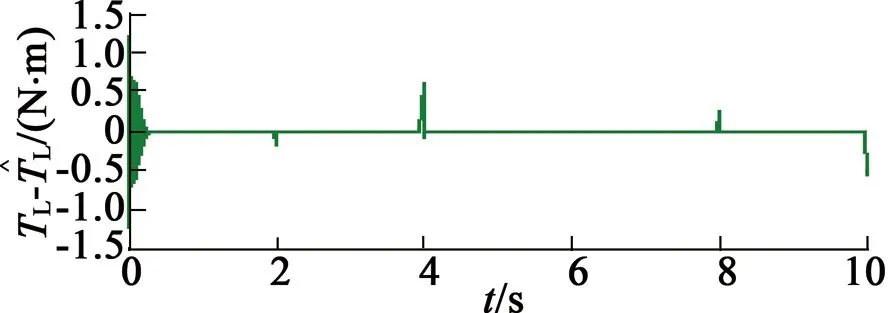
(f) 负载转矩估计误差

由第三种、第四种情况的仿真可以看出，负载转矩估计具有较小的误差，负载的自适应估计对于随机变化负载的估计也是有效的。

4.2 未知参数采用干扰观测器方法的仿真

采用干扰观测器进行负载转矩估计的PMSM指定速度位置跟踪的控制方案设计如图7所示。根据前面的控制参数调节原则，控制参数分别选择：k1=30，k2=320，k3=5 000，k4=40 000，k=25。指定速度控制变量设定为vd=sin (10t)。

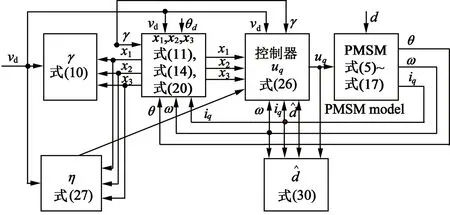
图7 采用干扰观测器的PMSM控制系统结构

在第五种情况下，未知负载转矩设定为固定常数TL=1 N·m，仿真结果如图8所示。在第六种情况下，未知负载转矩设定为TL=1-cos(πt/2)，仿真结果如图9所示。

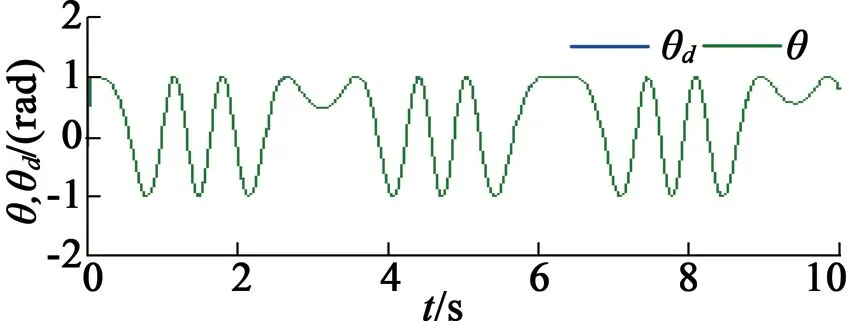
(a) 参考位置和实际位置

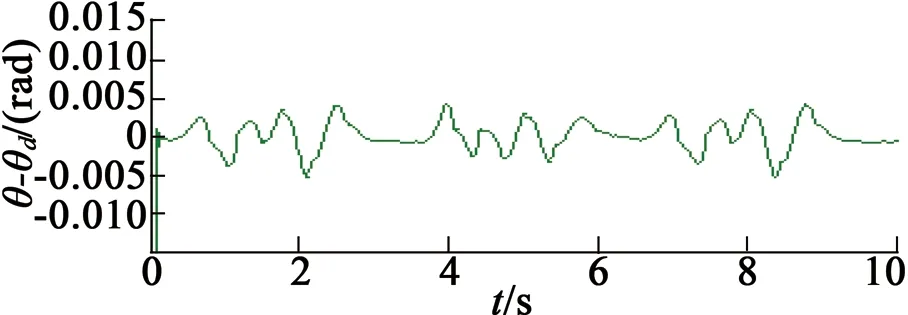
(b) 位置跟踪误差

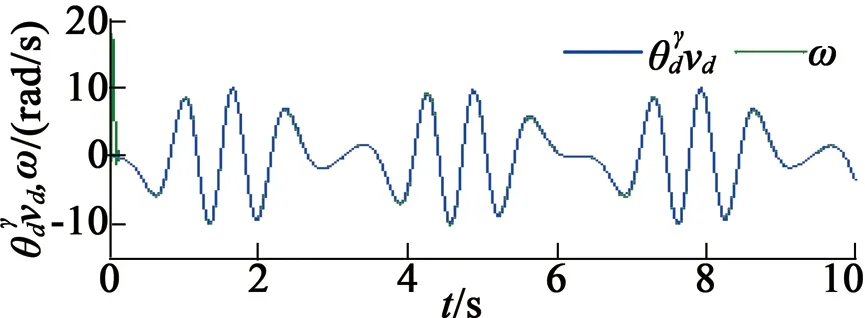
(c) 指定速度与实际速度

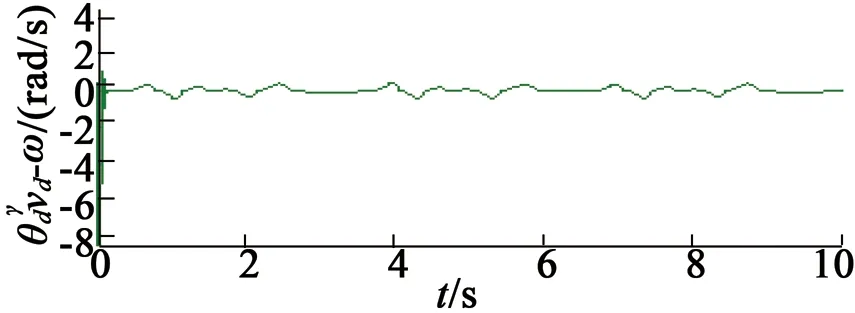
(d) 速度误差

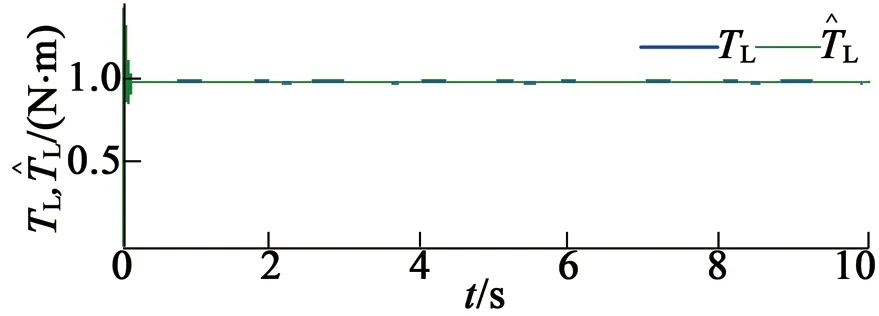
(e) 负载转矩与估计转矩

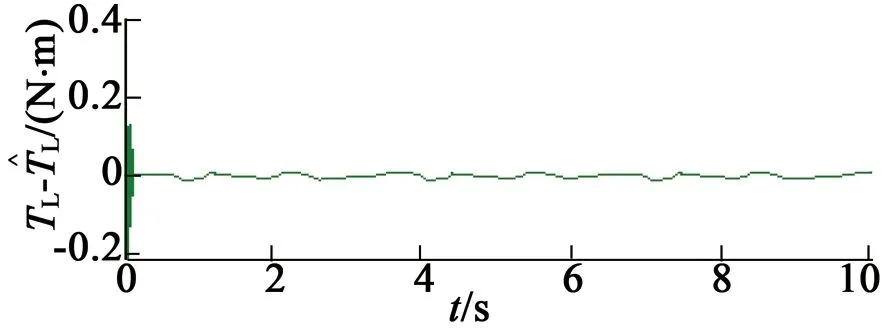
(f) 负载转矩估计误差

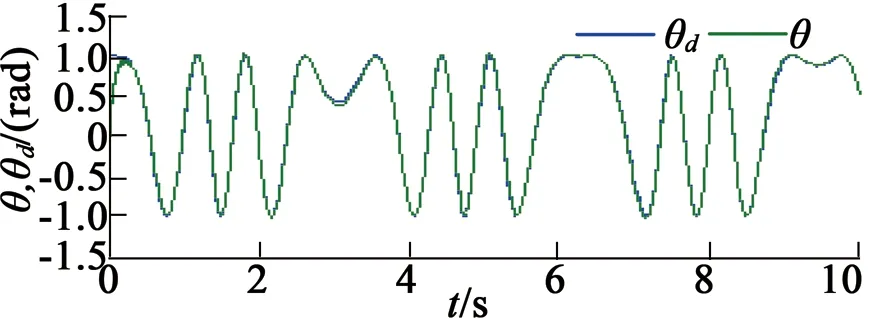
(a) 参考位置和实际位置

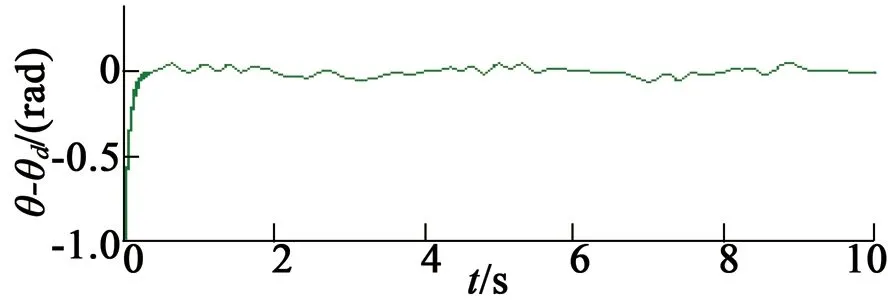
(b) 位置跟踪误差

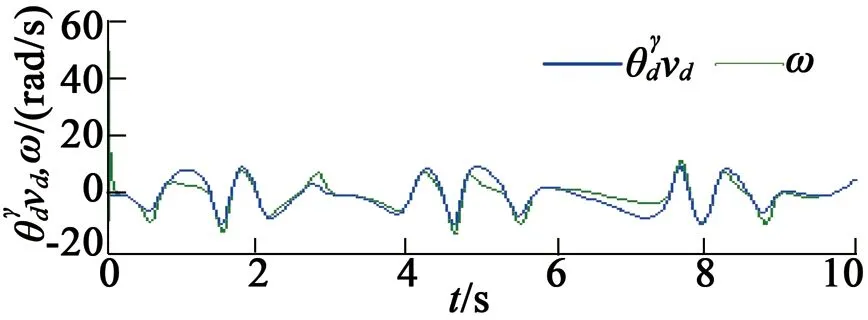
(c) 指定速度与实际速度

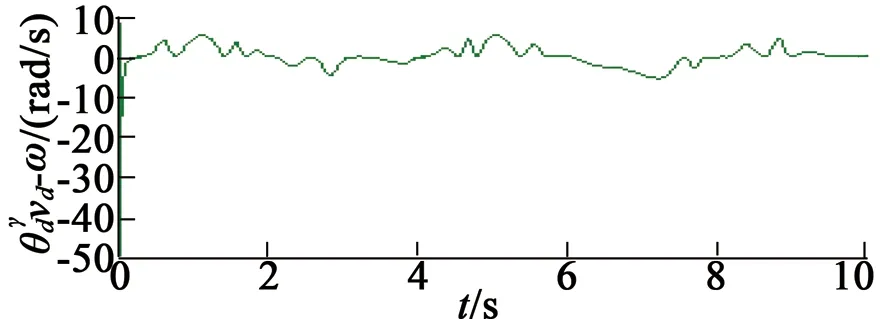
(d) 速度误差

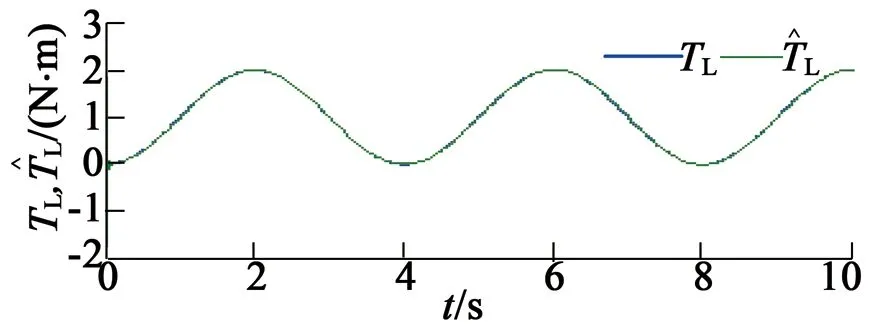
(e) 负载转矩与估计转矩

(f) 负载转矩估计误差

根据图8和图9中的仿真结果，可以得出如下结论：

1) 本文设计的自抗扰观测器参数调节简单便捷，相对于自适应估计具有更高的估计精度；

2) 自抗扰观测器简化了自适应反推控制设计，提高了位置跟踪控制的鲁棒性能；

3) 自抗扰观测器可以独立于控制器的设计，这相对于系统控制设计是非常有价值的。

4.3 仿真结果分析

根据上面各种情况的仿真，可以得出如下结论：

1) 在PMSM的位置跟踪过程中，通过速度指定方法可以增加位置跟踪控制的灵活性，速度控制自由度的引入对于调节PMSM位置跟踪的精度调节很有意义；

2) 基于自适应反推控制可以将速度指定方法引入PMSM位置跟踪，自适应估计方法可以有效估计未知负载转矩和指定速度的控制误差。

3) 自抗扰观测器可以估计PMSM的负载转矩，自抗扰观测器与本文中的自适应相比具有更快了响应速度和更高的估计精度。

5 结 语

本文将速度指定方法引入PMSM的位置跟踪控制中，实现了PMSM的速度指定位置跟踪控制。本文的主要贡献表现在如下方面：

1) 将速度指定控制方法引入PMSM的位置跟踪控制，速度指定方法将速度控制自由度引入位置跟踪控制，这可以增加位置跟踪的灵活性。

2) 自适应反推控制可以将速度指定方法与位置控制器的设计结合起来，同时通过自适应设计可以实现PMSM未知负载转矩和指定速度控制误差的自适应估计。

3) 为了进一步提高PMSM位置控制的精度，本文给出了一个新颖的自抗扰观测器设计方法。该自抗扰观测器可以独立于系统控制器进行设计，自抗扰观测器可以提高PMSM未知负载估计的响应速度和估计精度，这对于提高PMSM位置跟踪的精度具有重要的意义。

[1] 方一鸣， 任少冲， 王志杰，等. 焦晓红永磁同步电动机转速自适应模糊Backstepping 控制[J]. 电机与控制学报，2011,15(6): 98-102.

[2] M. MORAWIEC M. The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter[J]. IEEE Transactions on Industrial Information, 2013, 9(2): 1047-1055.

[3] MOHAMED Y A I. A hybrid-type variable-structure instantaneous torque control with a robust adaptive torque observer for a high-performance direct-drive PMSM [J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2491-2499.

[4] ERROUISSI R, OUHROUCHE M, Chen W H, TRZYNADLOWSKI A M. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost function[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7):2849-2858.

[5] GHAFARI-KASHANI A R, FAIZ J, YAZDANPANAH M J. Integration of non-linear H∞ and sliding mode control techniques for motion control of a permanent magnet synchronous motor[J]. IET Electric Power Applications, 2010, 4(4): 267-280.

[6] QI L, SHI H. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control[J], Neurocomputing, 2013, 115(4):23-30.

[7] PRASHANTH K V, GIRISHA N H. Position control of interior permanent magnet synchronous motor using adaptive backstepping technique[C]//International Conference on Advances in Computing, Communications and Informatics, 2013: 1718-1723.

[8] EL-SOUSY F M. Intelligent optimal recurrent wavelet elman neural network control system for permanent- magnet synchronous motor servo drive[J].IEEE Transactions on Industrial Informatics, 2013, 9(4): 1986-2003.

[9] LIN F J, YANG K J, SUN I F, CHANG J K. Intelligent position control of permanent magnet synchronous motor using recurrent fuzzy neural cerebellar model articulation network[J].IET Electric Power Applications, 2015, 9(3): 248-264.

[10] SKJETNE R, FOSSEN T I, KOKOTOVIC P V. Robust output maneuvering for a class of nonlinear systems[J].Automatica, 2004, 40(3): 373-383.

[11] KOKOTOVIC P V. The joy of feedback: nonlinear and adaptive[J].IEEE Control System Magazine, 1992, 12(3): 7-17.

[12] 王家军，赵光宙，齐冬莲．反推式控制在永磁同步电动机速度跟踪控制中的应用[J]．中国电机工程学报，2004，24(8)：95-98．

[13] YANG Z J, HARA S, KANAE S. An adaptive robust nonlinear motion controller combined with disturbance observer[J]. IEEE Transactions on Control Systems and Technology, 2010, 18(2): 454-462.

[14] TOMEI P, VERRELLI C M. Observer-based speed tracking control for sensorless permanent magnet synchronous motors with unknown load torque[J]. IEEE Transactions on Automation Control, 2011, 56(6): 1484-1488.

[15] CHEN W H. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706- 710.