不同占空比的无刷直流电动机反电动势过零点检测

张 云，王知学，谢 君，侯恩广

(1.山东交通学院 轨道交通学院，济南 250375； 2.山东交通学院 图书馆，济南 250375)

0 引 言

永磁无刷直流电动机是在有刷直流电动机的基础上发展起来的，不仅保留了有刷直流电动机良好的调速性能，还具有噪声低、体积小、控制灵敏、效率高、寿命长等特点[1]。无刷直流电机( 以下简称BLDCM)通过位置传感器获取转子位置信号，从而实现电子换相，然而位置传感器的存在会导致电机制造复杂、电路成本高、抗干扰性差和难以在高低温环境下工作等问题[2]。为此，提出了无位置传感器检测转子位置的方法，较为普遍的有反电动势法[3]、状态观测器法[4]和人工智能法[5]。其中反电动势法较为简单成熟，应用广泛，包括端电压法[6]和线反电动势法[7-10]。

本文基于线反电动势法实现反电动势过零点检测，将PWM斩波过程分为上桥臂开通、上桥臂关断而下桥臂续流、桥臂换相等三个工作状态，针对每个状态给出了基于反电动势检测转子位置的方法。根据斩波过程中不同占空比的维持时间，将反电动势采样的时刻分为小占空比续流时刻和大占空比通电时刻，并设计了带占空比阈值滞回的采样策略，给出了较为精确的低频斩波时的过零点计算方法。

1 反电动势法无位置控制原理

BLDCM系统的等效电路如图1所示。图1中：R，L分别为电机一相绕组的电阻和电感；ea，eb，ec分别为三相绕组的相反电动势；ia，ib，ic，分别为三相绕组的相电流；ua，ub，uc分别为三相绕组的相电压；N为三相绕组采用星形连接的中点；O点为参考电位。BLDCM三相绕组的端电压方程如下：

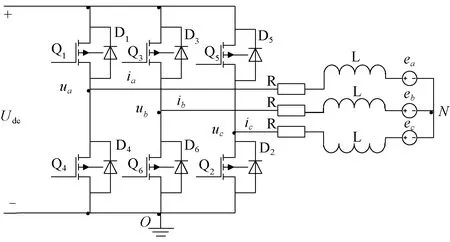
图1 BLDCM系统等效电路

(1)

理想BLDCM的反电动势、相电流及霍尔位置信号的关系如图2所示，霍尔位置传感器安装在定子齿的中心线上，θ为转子相对于定子A相绕组轴线而转过的电角度，将一个电周期分为6个扇区S1～S6，每个扇区为60°电角度，不同的扇区对应不同的霍尔位置传感器，也对应不同的输出相序，如在S1扇区，C相上桥臂Q5导通，B相下桥臂Q6导通，进入S2扇区，C相上桥臂Q5关断，A相上桥臂Q1开通，B相下桥臂Q6开通。随着转子位置的变化，霍尔信号发生相应的变化，根据霍尔信号的变化来控制功率转换电路的开关顺序，输出相应的电流ia，ib，ic，驱动电机运行。

BLDCM的气隙磁场波形为梯形波，如图3所示，其中α为电角度。

图3 BLDCM气隙磁场波形

BLDCM的反电动势如下式：

(2)

式中：K为与电机结构相关的参数；B(θ)为气隙磁密分布，对于BLDCM而言，B(θ)为梯形波，ω为电机转速。

从式(2)可以看出，当图3中气隙磁场波形为平顶波时，反电动势为平顶波，当磁场由高变低出现过零点时，其反电动势也出现过零点。如图2所示，采用两相导通控制BLDCM时，每一时刻都有两相绕组的反电动势为平顶波，另外一相的反电动势为倾斜上升或者下降的波形，为不驱动的悬空相。图1中绕组端点电压与反电动势和中心点N的电压之间的关系如式(1)所示，采用星形接法，三相绕组的电流之和为零，导通两相的反电动势大小相等，符号相反，将式(1)三个方程相加，得到不导通相的反电动势ek与三相绕组的端点电压和中点电压的关系：

ek=ua+ub+uc-3uNO

(3)

不导通相的电流为零，则该相绕组端点电压、反电动势和中性点电压关系：

ek=uk-uNO

(4)

将式(4)代入式(3)，消去中心点电压uNO，得到不导通相反电动势：

(5)

当不导通相的反电动势过零时，即ek为0，得：

(6)

设A相为不导通相，则ua=uk，则式(6)变为：

(7)

当B，C两相为导通相，A相悬空时，若检测到电机三相绕组端点电压满足式(7)时，则A相绕组反电动势处于图2的过零点处，转子再转过30°电角度后，控制A相绕组开通。基于反电动势法的无位置传感器控制，就是通过检测电机悬空相绕组的反电动势过零点的位置实现对电机的控制。

2 基于PWM的反电动势位置检测

对于两相导通的BLDCM控制方法，一相上桥臂PWM斩波，另一相下桥臂保持直通，第三相为悬空的不导通相。在PWM斩波过程中，有三个导通的状态：上桥臂开通的通电状态，上桥臂关断而下桥臂续流状态，两桥臂换相状态。针对PWM斩波过程的三个状态，分析基于反电动势过零点检测的特点。

2.1 上桥臂开通的通电状态

设A相上桥臂PWM斩波，B相下桥臂直通，C相上、下桥臂都不导通，检测C相绕组的反电动势。此时图1的等效电路如图4所示，其中udc为供电电压，I为相电流，VSW为开关管的导通压降，R为相绕组电阻，L为相绕组电感，ea与eb分别为相绕组的反电动势，N为相绕组中点。ea与eb大小相等，统一用E表示，A相电压uAN减B相电压uBN得BLDCM简化的数学模型：

图4 导通时的等效电路

uAN-uBN=2RI+2LpI+2E

(8)

图4电路的方程：

udc=2RI+2LpI+2E+2VSW

(9)

由于ia=-ib，ea=-eb，则式(1)中上两个式子相加得：

uAN+uBN=0

(10)

由式(10)可知，两相的相电压相等，符号相反，如果忽略开关管的导通压降，电机中点N的电压与A，B两相绕组端点的电压关系：

(11)

两相导通时电机中点的电压等于电源电压的一半，由式(7)可知，不导通相C的反电动势过零时，其端点电压uC等于中点电压uN，即当uC等于电源电压的一半时，C相绕组反电动势过零。

当检测到C相绕组的反电动势过零后，转子再旋转30°电角度，即可开通C相。如图2所示，当检测到C相绕组端点电压uC与uN的差值由正变负时，说明C相绕组反电动势由正变负，转子转过30°电角度之后，应该关断B相下桥臂而开通C相下桥臂；反之，当检测到C相绕组的端点电压uC与uN的差值由负变正时，转子转过30°电角度后，则要关断B相上桥臂而开通C相上桥臂。

2.2 上桥臂关断而下桥臂续流状态

在PWM斩波过程中，当一相的上桥臂关断，绕组电流通过下桥臂的二极管续流导通时，如图1所示，设Q1关断，Q4，Q6导通，等效电路如图5所示，设续流二极管的压降与MOSFET的导通压降相等，则简化的数学模型：

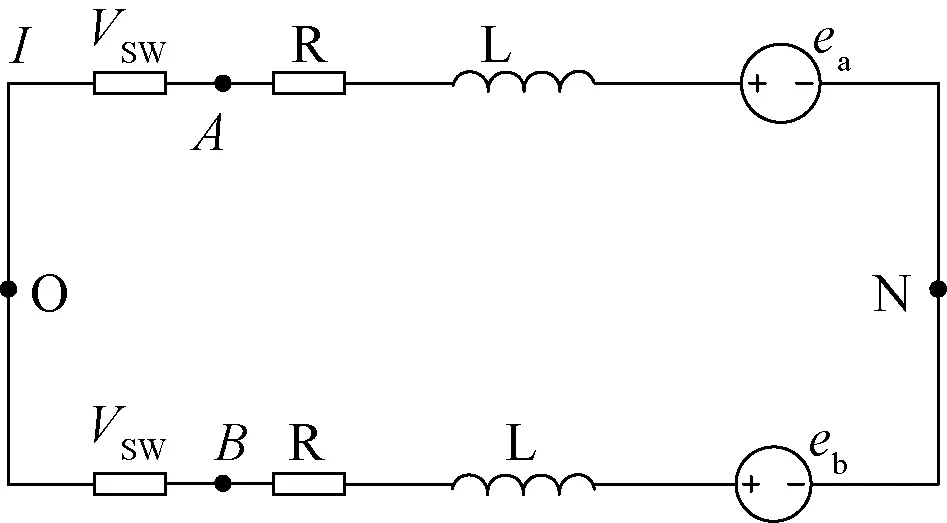
图5 续流导通时的等效电路

0=2RI+2LpI+2E+2VSW

(12)

绕组中点的电压：

uN=uO=0

(13)

A相和B相中点对地的电压：

(14)

由式(7)得，不导通相的反电动势过零点时的电压：

(15)

当不导通相C的反电动势过零时，其端点电压uC为零。如图2所示，当PWM斩波的续流期间C相端点的电压由正变零时，C相绕组的反电动势出现过零点，转子转过30°电角度后，关断B相的下桥臂，开通C相的下桥臂；反之，当检测到C相端点的电压由零变正时，则C相绕组的反电动势出现过零点，转子转过30°电角度后，开通C相上桥臂，关断B相的上桥臂。

2.3 桥臂换相的状态

桥臂换相是指一相桥臂由上桥臂斩波或下桥臂直通切换到上、下桥臂都不导通，而开通另一个不导通相的过程。由于电机电感的续流作用，一相桥臂的开关管由导通变为关断后，电流要续流一段时间。如图6所示，以C相桥臂的对地电压uC的波形为例，粗线部分为电流续流时的电压波形。续流1为C相上桥臂由斩波开通变为关断时uC的电压波形，当图1中的上桥臂Q5关断后，电流要从Q2向上续流，此时C相端点电压uC变为0；续流2为C相下桥臂由直通变为关断时uC的电压波形，当图1中的上桥臂Q2关断后，电流要从Q5向上续流，此时C相绕组的端点电压uC变为电源电压。

图6 换相续流过程

由于桥臂换相后，不导通相绕组要经过电流续流状态之后才能变为悬空状态，而在换相续流期间，悬空相绕组的端电压为零或者电源电压，无法检测反电动势，所以反电动势检测转子位置时应该避开这段时间。

3 基于反电动势的转子位置检测

3.1 基于PWM占空比的反电动势检测

基于PWM的电机控制算法是通过不断改变PWM斩波的占空比而实现对电机的控制，反电动势过零点的检测就是在PWM斩波的过程中实现的。图7为PWM斩波时的波形，上桥臂开通的通电状态的时间为TON，上桥臂关断的续流状态的时间为TOFF。在PWM斩波的过程中，设单片机模拟采样、保持及转换的时间为tAD，单片机PWM输出由低变高到功率管完全开通的时间为tOPEN，则要完成绕组端电压采样所需的时间至少为(tAD+tOPEN)。

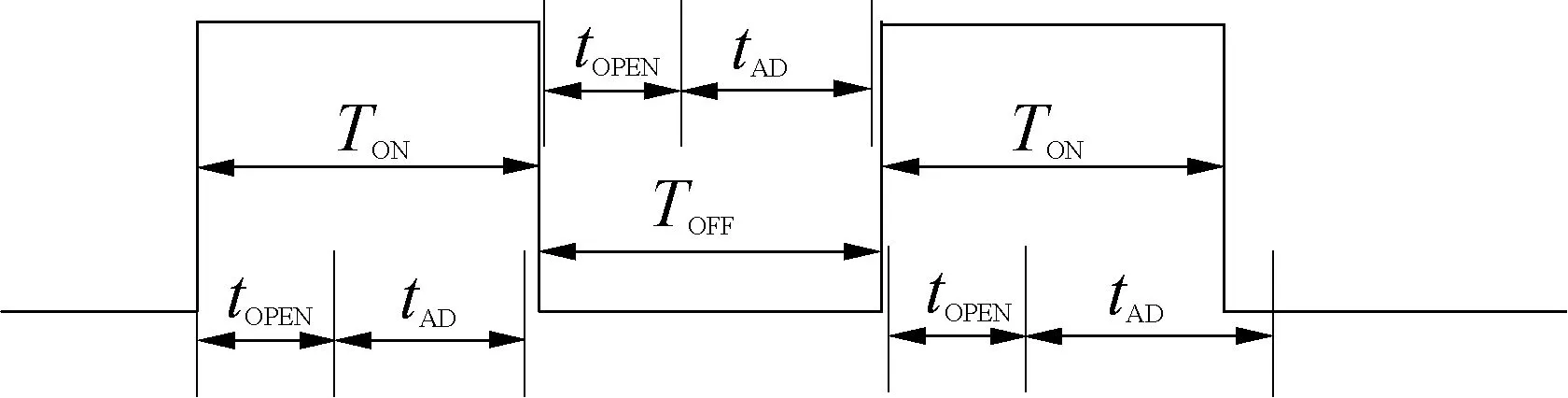
图7 PWM斩波时的采样时间

要根据PWM斩波过程中占空比的大小来选择电机绕组端点电压的采样时刻。当TON>(tAD+tOPEN)时，可采用上桥臂开通通电状态来完成采样，并用式(11)来计算过零点；反之，当TOFF>(tAD+tOPEN)时，可采用上桥臂关断的续流状态来采样，用式(15)来判断绕组的过零点。所以基于反电动势法的过零点位置采样对PWM周期有一定的要求，至少要保证占空比为50%时的高电平或低电平的保持时间超过(tAD+tOPEN)。

3.2 带占空比阈值滞回的采样策略

基于反电动势法的BLDCM无位置传感器转子检测方法要根据PWM斩波的占空比大小来选择合适的采样点和检测算法。一般功率管的开通时间tOPEN<2 μs，模拟采样的时间tAD<8 μs，确保反电动势采样的时间大于10 μs即可，即PWM的斩波周期为20 μs。在电机控制中，PWM斩波频率一般不高于20 kHz，即斩波周期不小于50 μs，完全能够满足采样要求。当PWM占空比较小时，在上桥臂关断续流时采样悬空相过零点；当PWM占空比由小变大，超过了40%时，切换到上桥臂开通的通电状态采样悬空相过零点；当PWM占空比由大逐渐变小到30%时，再切换到上桥臂关断续流时采样悬空相过零点。

以C相不导电为例，当PWM占空比较大时，在上桥臂开通时采样过零点，此时C相采样值uC为反电动势。当uC-(uA+uB)/2的差由正变负时，C相反电动势出现过零点，转子转过30°电角度后的下一个换相时刻将控制C相下桥臂导通；反之，当uC-(uA+uB)/2的差由负变正时，C相反电动势出现过零点，转子转过30°电角度后的下一个换相时刻将控制C相上桥臂导通。当PWM占空比较小时，采用上桥臂关断续流时采样过零点，当C相中点电压由正变0时出现过零点，转子转过30°电角度后将控制C相下桥臂开通；反之，当C相中点电压由0变正时出现过零点，转子转过30°电角度后将控制C相上桥臂开通。

3.3 低频斩波时的过零点计算

为了给反电动势检测留出足够的采样时间，应尽量降低PWM的频率，但这会减少反电动势检测的频次，降低检测精度，随着电机转速的升高，检测频次进一步减少。为了提高电机高速运行时反电动势的检测精度，设计了考虑反电动势电压的过零点计算方法，如图8所示。图8中，Q0(t0,u0) 为实际的反电动势过零点的时刻和对地电压，Q1(t1,u1) 和Q2(t2,u2) 分别为过零点前和过零点后的实际采样点的时刻和对地电压，由于反电动势近似为线性变化，所以可以根据Q1和Q2点的时间和电压估算实际的过零点时间t0，由式(11)得：

图8 反电动势采样点

进而得到过零点时间t0：

(16)

4 实验研究与分析

4.1 实验平台介绍

为了验证无位置传感器的转子位置检测方法的可行性，搭建了电机及控制的测试实验平台，如图9所示，左侧为测功机的制动器，中间为被控的BLDCM，右侧为控制实验板。电机的额定电压为24 V，额定功率为100 W，最高转速为4 000 r/min，控制实验板的主处理器为STM32F405。

图9 电机测试平台

4.2 小占空比的反电动势过零点检测

图10为占空比为30%时的反电动势检测波形，上方曲线3为一相桥臂中点的对地电压，中间曲线1是用单片机一个引脚的电平变化表示检测到悬空相反电动势过零点，下方曲线2是单片机输出的斩波相的PWM波形。

图10 占空比为30%时的反电动势检测波形

图10(a)的中间曲线1的电平从低跳变到高的时刻，表示采样到反电动势的过零点，可以看出，采样时刻是PWM波形输出低电平的时刻。曲线1处于低电平时，PWM波形处于低电平的时间段内，曲线3的变化较大，但其幅值基本都大于0；曲线1跳变为高电平时，在PWM低电平的时间段内，曲线3的幅值基本接近于0，且之后的PWM低电平时间段内，反电动势基本为0，这说明PWM低电平时刻采样是有效的。

如图10(b)所示，检测到曲线3反电动势过零点后，曲线1即输出电平跳变，表示出现了过零点。可以看出，过零点的检测基本均匀，可以用于控制电机运行。由于PWM占空比较低，电机运行转速不高，PWM斩波频率相对较高，基本能够满足检测精度需求。

4.3 大占空比的反电动势过零点检测

图11为占空比为70%时的反电动势检测波形，上方曲线3为一相桥臂中点的对地电压，中间曲线1是用单片机一个引脚的电平变化表示检测到悬空相反电动势过零点，下方曲线2是单片机输出的斩波相的PWM波形。

图11 占空比为70%时的反电势检测波形

图11(a)的中间曲线1的电平跳变时刻，表示采样到反电动势的过零点，可以看出，采样时刻是PWM波形输出高电平的时刻。曲线1处于低电平时，PWM波形处于高电平的时间段内，采样反电动势电压检测到过零点后，单片机控制某一输出引脚电平跳变，指示出现了过零点。

如图11(b)所示检测到曲线3反电动势过零点后，曲线1即输出电平跳变，表示出现了过零点。可以看出，过零点的检测也不均匀，时间长短不一，精确性和一致性不好，这是由于电机转速较高，在一个换相周期内斩波次数较少。

图11(c)为利用式(16)计算的反电动势过零点，曲线3为一相桥臂的对地电压，曲线1电平跳变的时刻是根据式(16)计算的反电动势过零点而输出的实际控制换相时刻波形，曲线2为PWM控制的波形。可以看出，此时的曲线1较图11(b)中的曲线1更为均匀，一致性和精确性更好。

5 结 语

本文详细阐述了BLDCM反电动势检测转子位置的方法，根据PWM斩波控制的特点，将斩波过程分为上桥臂开通、上桥臂关断而下桥臂续流、桥臂换相等三个工作状态，并针对每个状态给出了基于反电动势检测转子位置的方法。根据PWM不同占空比下的维持时间，将反电动势采样的时刻分为小占空比续流时刻采样和大占空比通电时刻采样，并设计了带占空比阈值滞回的采样策略，给出了较为精确的低频斩波时的过零点计算方法。最后，实验测试证明了本文给出的反电动势过零点检测方法的合理性。