凭分吹草动 我自涛声依旧
——2017年高考三角函数题型回顾与展
■江西省丰城中学 吴爱龙
纵观近几年高考全国卷,三角函数部分一般是一大一小两道试题。如果不考大题,则会考三道小题;考查内容主要涉及三角函数求值、三角函数的图像与性质、三角恒等变换、解三角形。2 0 1 7年高考大纲提出了对“数学文化”知识考查的明确要求;对能力要求的内涵进行了修改,增加了基础性、综合性、应用性和创新性的要求,强调考查同学们的数学思想、数学能力、数学的科学与人文价值,更加注重了对同学们数学综合素养的考查。尽管考纲作了较大调整,但由于三角函数属传统章节,考查的内容几乎没太大的变动。
聚焦1 三角函数的图像
例1 (1)(2 0 1 7年课标Ⅰ卷)已知曲线

结论正确的是( )。
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线

B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线2C.把1上各点的横坐标缩短到原来的,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线2
(2)(2 0 1 7年天津卷)设函数f(x)=2 s i n(ω x+φ),x∈R,其中ω>0,|φ|<π。若,且f(x)的最小正周期大于2 π,则( )。

解析:(1)若把曲线C1上各点横坐标伸长到原来的2倍(纵坐标不变),便得y=c o s,无论左右怎么平移不可能得到曲线C2,排除选项A、B。当把曲线C1上各点的横坐标缩短到原来的(纵坐标不变)后,得到曲线y=c o s2x,再将其向左平移个单合题意。由2 π=3 π,得ω=2,排除选项C、ω 3 D。若选A,则,此时,符合题设,而选项B不合题意,故答案为A。


点评:准确画出y=s i nx、y=c o sx、y=t a nx及y=As i n(ω x+φ)的图像是考试大纲的基本要求,对于函数y=As i n(ω x+φ)还必须掌握“五点作图法”与“变换作图法”,了解其物理意义及参数A、ω、φ对函数图像变化的影响。变换法作图包括振幅变换、周期变换、相位变换,振幅变换较好掌握,后两者容易出问题。对于周期变换与相位变换建议先相位后周期变换,否则平移的长度单位易出错。由函数y=f(ω x)的图像要得到函数y=f(ω x+φ)的图像必须是左(右)平移 φ 个
ω
单位,而不是|φ|个长度单位。五点法作图应抓准五个关键点,尤其是其中三个零点。第一个零点图像特征是由下而上,第二个零点是由上而下。在已知函数图像求函数解析式时,如果从图上把握不住图像特征,建议不用零点代入求初相φ的值。如本例第二小题在得出之后,利用条件
求φ时,就无法排除选项B了。
聚焦2 三角函数的性质
例2 (1)(2 0 1 7年课标Ⅲ卷)设函数
,则下列结论错误的是( )。称

(2)(2 0 1 7年浙江卷)已知函数f(x)=s i n2x-c o s2x-2 3 s i nxc o sx,求f(x)的最小正周期及单调递增区间。数不单调,D错误,故选D。)的最小正周期是解得的单调递增区间是[π+kπ,2π+kπ],k∈Z。63



点评:三角函数的性质包括三角函数的定义域、值域、最值、周期性,以及单调性、奇偶性与对称性。判断函数的周期性可用定义或套 用Ac o s(ω x+φ)的 最 小 正 周 期 为 T的最小正周期为T=若要判断直线x=a是否为函数f(x)=As i n(ω x+φ)或f(x)=Ac o s(ω x+φ)的对称轴,只需判断f(a)=±A或f'(a)=0是否成立;若要判断点(a,0)是否为它们的中心,只要判断f(a)=0是否成立。函数y=f(a-x)是一个复合函数,欲求其单调递增区间必须先求函数的定义域进而求函数y=f(x)的递减区间;若函数y=f(x+a)为偶函数,有f(-x+a)=f(x+a),则函数y=f(x)的图像关于直线x=a对称。若函数y=f(x+a)为奇函数,有f(-x+a)=-f(x+a),从而知函数y=f(x)的图像关于点(a,0)成中心对称。此外,若函数y=f(x)满足条件f(a+t)=f(b-t),t∈R,则函数y=f(x)的图像关于直线x=对称。而函数y=f(a+x)与y=f(b-x)的图像关于直线对称,前者属函数图像的自身轴对称问题,后者是两个函数图像之间的相互对称问题,应严加区别。此外,还应掌握翻折变换。函数y=f(|x|)是偶函数,图像关于y轴对称,在y轴右侧的图像保留,左侧原有图像去掉后再将右侧图像关于y轴翻折过去。
聚焦3 三角函数的变换
例3(2 0 1 7年山东卷理科)已知函数


(1)求ω;
(2)将函数=f(x)的图像上各点的横坐标扩大到原来的2倍(纵坐标不变),再将得到的图像向左平移个单位,得到函数y=g(x)的图像,求g(x)在小值。又0<ω<3,所以ω=2。

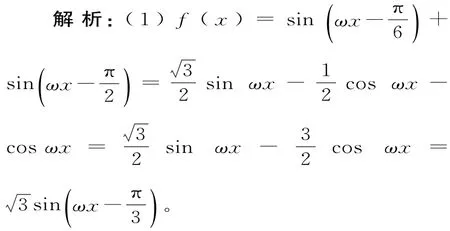

(2)由(1)知,将其图像上各点横坐标扩大到原来的2倍(纵坐标不变),得函数;再将图像向左平移π个单位,得g(x)=4



点评:三角函数的恒等变换是高考的必考内容,它渗透于三角函数的求值与化简、图像与性质、解三角形与平面向量等各种题型之中。三角恒等变换既要掌握和(差)角公式、二倍角公式,又要会套用积化和差、和差化积与半角公式。此外,还必须掌握诸如常值代换、整体处理、凑角、升(降)幂等常用技巧。公式等是常用公式,此外,公式及其变形也经常用到。本例函数f(x)还可以直接套用和差化积公式来化简,f(x)=也非常简捷。



聚焦4 解三角形的问题
例4 (1)(2 0 1 7年山东卷理科)在△A B C中,角A、B、C的对边分别为a、b、c,若△A B C为锐角三角形,且满足s i nB(1+2 c o sC)=2 s i nAc o sC+c o sAs i nC,则下列等式成立的是( )。
Aa.=2b Bb.=2a
C.A=2B D.B=2A
(2)(2 0 1 7年全国新课标Ⅰ卷理科)已知△A B C的内角A、B、C的对边分别a、b、c,

①求s i nBs i nC;
②若6 c o sBc o sC=1,a=3,求△A B C的周长。
解析:(1)由题设知s i nB+2 s i nBc o sC=s i nAc o sC+s i n(A+C),又s i nB=s i n(A+C),因此,有2 s i nBc o sC=s i nAc o sC。因为c o sC≠0,所以2 s i nB=s i nA,即2b=a,故选A。

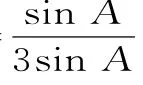

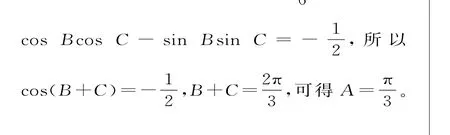
(2)①由题设条件可得1a cs i nB=2由正弦定理得s i nCs i nB=,故s i nBs i nC=。又a=3,代入b cs i nA6 2c m。在容器中注入水,水深为1 2c m。现有一根玻璃棒l,其长度为4 0c m,容器厚度、玻璃棒粗细均忽略不计,将l放在容器中,l的一端置于点E处,另一端置于侧棱G G1上,求l没入水中部分的长度。
解析:(1)将正六边形分割为6个全等的得b c=8。由余弦定理得,所以得b+c=3 3,故△A B C的周长为3+3 3。
点评:解三角形常涉及正弦定理、余弦定理(勾股定理)、射影定理、内角和定理以及三角形面积公式等知识,必须熟记。考查题型包括求角、求边长、求函数值、求面积与周长的取值范围或最值问题。此外还要熟练掌握一些常见的三角恒等变换,变换的方向是消去“角度差异”、“名称差异”与“次数差异”。
聚焦5 三角文化与素养
例5 (1)(2 0 1 7年浙江卷)我们古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度。祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S6,S6=。
(2)(2 0 1 7年江苏卷)如图1,水平放置的正四棱台形玻璃容器的高为3 2c m,两底面对角线E G,E1G1的长分别为1 4c m和
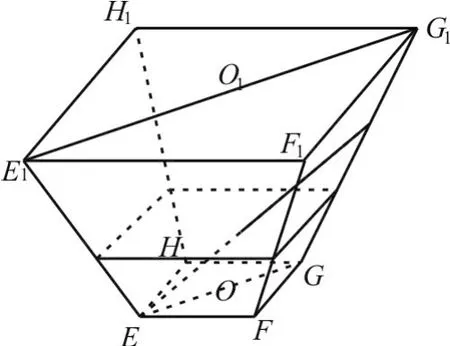
图1


(2)作其对角面E E1G1G,如图2。再作G K⊥E1G1于K,作NM⊥E G交其延长线于M,则△GMN与△G1K G相似。G中+M,3 x由=设在3勾)x2M股+R。N t定(=4理△x 4E x知)M2,(1N则= 4 4 02,解得x=6。


图2
设EN与水面交
点为P,作P Q⊥E G于Q,则由△E P Q与△E NM相似知E P=2 0。

故玻璃棒l没入水中部分的长度为2 0c m。
点评:数学文化与数学素养的考查是新一轮高考命题大纲的明确要求,以此为背景命制试题既能考查知识的应用,又能使同学们感受到我国古代灿烂的数学文化。
通过以上对2 0 1 7年高考中的三角函数高考题型回放与聚焦,我们不难看出三角函数题型是较为稳定的,并无大起大落。认真研读2 0 1 8年全国统一考试大纲(理科)后,预测2 0 1 8年高考三角函数题型仍将如此,不会有大的变化或举动。希望同学们迎考学习时,应紧扣考试大纲,回归课本,瞄准考点,弄清知识点,淡化技巧,不搞“题海战术”,回避难题与偏题。由于在高考《考试大纲》“总纲”中特别强调“立德树人”育人功能,通过数学史上典型事例,渗透中华优秀传统文化的因素,使同学们感受中华文明的博大精深,因此对涉及三角的数学文化试题仍应多加关注。此外,应注意三角函数与数列、导数的综合问题,三角函数与均值不等式的交汇而命制的最值或取值范围问题,在解三角形中,应关注角平分线、中线、外接圆、内切圆等几何概念,应了解测量中的方位角、仰角与俯角等术语,还应重视正、余弦定理与三角形面积公式等在平面多边形中的拓展应用。总而言之,对三角函数的学习,只要多做常规题,便可轻松得分。三角函数命题考向预测以一言而蔽之,即:“任凭风吹草动,我自涛声依旧。”

