中职数学教学中的情境创设
陈立斌
摘 要:中职数学是中职学校重要的文化基础课,是学好专业课的基础。然而,中职学生普遍数学基础知识薄弱,对数学学习缺乏兴趣。本文就如何提高中职数学教学效果,激发学生学习数学的兴趣,从教学情境创设方面,谈谈自己的教学经验。
关键词:中职数学;教学情境;措施
中职学生普遍文化课基础薄弱,尤其数学知识比较缺乏,不仅表现为数学知识掌握不扎实,而且对数学学习缺乏兴趣。要想提高中职学校的数学教学效果,培养学生对数学的学习兴趣很重要。课堂是教学的主阵地,每一次课堂教学都是从情境创设开始的,有效的情境能够激发学生学习数学的兴趣。笔者结合自己在中职数学教学工作中的经验,谈一谈中职数学教学中创设情境的方法。
一、以数学游戏创设教学情境
数学游戏是一种运用数学知识的大众智力娱乐活动,把有趣的数学游戏引入数学教学中,在具体的情境中初步认识对象的特征,用游戏激活课堂。
例如,在“两条直线的位置关系”一课的教学,教师可以让学生玩“两人的双手各被两根绳子交叉绑住,不解开绳子或剪短绳子,将两人分开”的游戏,让学生发挥自己的想象力寻找解决方案。学生经过努力未能解决这个问题,会向教师寻求帮助,这样就把学生的注意力拉回了课堂。学生在教师的指导下,成功解决问题,体会到成功的喜悦,从而激发了学生学习的兴趣。教材上的概念、性质,多是以较抽象的结论或精炼的数学语言呈现的,学生理解起来会有一定的困难,而游戏的方式可以改变知识的呈现方式,利用学生头脑中已有的知识或相关经验,为学习提供有利条件。
二、以数学故事创设教学情境
数学理论的发展史中,数学故事丰富多彩,把数学故事引入课堂中,极大地丰富了数学教学内容,激发了学生学习的积极性。因此,在数学教学中适当结合数学故事有利于培养学生对数学的兴趣,帮助学生克服消极倾向。
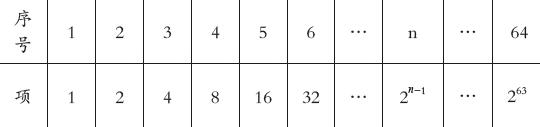
例如,在“数列”一课的教学,引入国王与麦粒的故事。国王要奖励国际象棋的发明者,让发明者自己提出奖励要求,发明者提出的要求是:“请在棋盘的第1个格子里放1颗麦粒,在棋盘的第2个格子里放2颗麦粒,在第3个格子里放4颗麦粒,在第4个格子里放8颗麦粒,以此类推,每个格子里放置的麦粒都是前一个格子的2倍,直到第64个格子。”国王听了很高兴,觉得这太容易了,你觉得国王是否真的满足发明者的要求?学习了数列知识后,学生就可以帮助国王回答这个问题。从棋盘第1个格子到第64个格子的麦粒:
从棋盘第1个格子到第64个格子麦粒的总数:Sn=1+2+4+8+16+…+…+263=18446744073709551615。一斤麦子有26000粒麦粒,那么18,446,744,073,709,551,615÷26,000÷2000=354,745,078,340.568 (吨) 。
这是一个非常有趣的数学故事,包含了等比数列的公比、首项、通项公式、等比数列求和等数学知识。学生在感受数学故事的同时,又学到了数学知识。
三、以数学历史创设教学情境
数学是一门古老的学科,历史悠久,源远流长。中国古代的数学家为数学的发展创立了丰功伟绩。成书东汉时期的《九章算术》是中国古代最早的数学著作,随后出现了祖冲之、秦九韶公式(国外称海伦公式)等,这些都比西方数学早几百年。把数学历史引入数学教学中,将会激发学生的爱国主义情怀,树立民族自豪感。
四、以数学实验创设教学情境
数学实验就是教师依据学生的实际能力,结合教材知识,运用一定的教学道具和手段,引导学生积极实验,并且在教学过程中组织学生主动获取知识和构建知识,培养其数学思维、数学技能和数学素质。
例如,在“指数函数”教学中,教师可以让学生完成关于折纸的实验。
师:谁能告诉我珠穆朗玛峰有多高?
生:大约8848米。
师:那么大家有没有想过一张纸经过有限次对折之后厚度会达到甚至超过珠峰的高度呢?下面我们来分析一下这个问题,将一张纸从中间对折,设对折次数为x,对折后纸的层数为y,y与x之间构成一个函数关系,你们能写出x与y之间的函数关系式吗?
生:y与x之间的关系式可以表示为:y=2x。
师:借助计算机算一下,当纸的厚度为0.03mm时,对折32次,它的厚度能达到多少?会超过珠峰吗?
生:当x=32时,y=4294967296,超过了珠峰的高度。
这个实验把指数函数的相关知识融入其中,学生通过全程参与实验,从函数关系式的建立到得出对折32次纸张的厚度,最终的结果让学生匪夷所思,感受到数学知识的博大精深,从而激发学生学习数学的兴趣。
要想提高中职学校的数学教学效果,首先要吸引学生,激发学生学习数学的兴趣。中职数学教师要在创设教学情境上多下工夫,把学生的注意力吸引到课堂教学上来,培养学生学习数学的興趣。兴趣是最好的老师,只要学生有了学习兴趣,中职数学教学工作一定能圆满开展,达到预期效果。
参考文献:
[1]鲍分民.运用数学游戏激活课堂[J].考试周刊,2013(84).
[2]毕伟华,唐艳敏.基于数学故事在中学数学中的实践应用研究[J]. 数学学习与研究(教研版),2017(7).

