基于Normative算子的HFS数值延拓方法及多属性决策应用
孙贵东, 关 欣, 衣 晓, 赵 静
(海军航空大学航空作战勤务学院, 山东 烟台 264001)
0 引 言
多属性决策是多传感器电子侦察情报融合处理的关键环节,特别对于决策层融合来讲,融合中心通过融合来自各信源的独立属性判决,给出多传感器融合结果。随着电子侦察情报的多源异类,导致各信源上报的独立属性判决往往具有不确定性,这就造成了融合中心多属性决策的模糊性。为了解决属性决策的模糊性问题,本文引入近年来发展起来的犹豫模糊集(hesitant fuzzy set,HFS)来处理带有模糊信息的多属性决策问题[1-3]。
2010年文献[4]引入了HFS的概念,本质上HFS与直觉模糊集和模糊多重集之间的关系紧密,也可以看成是二型模糊集的特例。HFS的产生是因为其隶属度不是像直觉模糊集那样由于误差幅度的不确定性和二型模糊集那样由一系列离散可能值的程度进行描述,而是在一些可能值之间犹豫不定。例如对于侦察情报上报的某型飞机的描述,决策A认为其隶属于Ⅰ型飞机的隶属度是0.4,而决策B认为其隶属于Ⅰ型飞机的隶属度为0.6,则最后关于隶属于Ⅰ型飞机的决策就会在0.4和0.6之间犹豫不定,此时就可以用HFS表示,即h={0.4,0.6}。尽管HFS提出至今不足10年的时间,但由于其在处理模糊信息领域的优越性,得到了学者的广泛关注,在距离、相似度度量、集成算子、运算方法、关联系数等方面取得了一系列研究成果[5-14]。文献[5-6]首先定义了HFS之间的距离、相似度和关联系数度量,并基于现有模糊集的度量方法提出了一系列HFS距离、相似度和关联系数度量计算式;文献[7-8]分析了文献[5-6]提出的HFS距离度量方法,并指出其在有些条件下不满足三角不等式,提出了改进的距离度量方法;最近文献[9]又提出了新的HFS相似度度量方法;文献[10-12]则提出了HFS集成算子的概念,并给出了各种HFS集成算子样式,相继文献[13]重点讨论了HFS的除法、减法运算;之后文献[14]指出了现有的关联系数的不足,并提出了新的关联系数,使其与统计学关联系数更贴近。HFS不仅在数学概念上取得了进展,在属性决策[15-21]、聚类分析[22-25]、模式识别[26-27]、特征提取[28]、语义计算[29-31]等领域HFS也得到了广泛的应用。
上述文献较好地分析了HFS的性质和应用,但是通过分析HFS的性质发现,其各种运算方法基本上都是基于HFS隶属度可能值的数值个数相同的前提,如果隶属度可能值的数值个数不一致,上述方法的都无法直接运算,因此关于HFS隶属度可能值的数值个数的统一问题值得研究。现有的HFS隶属度可能值的数值个数统一方法主要是文献[5]提出的基于隶属度最大、最小进行NE的乐观、悲观法。此外,文献[15]提供了一种0.5隶属度NE方法,文献[21]和文献[32-33]改进了乐观、悲观法提出了基于态度的η法NE方法。文献[34]认为延拓增加的元素应该是HFS中原有的元素,这样最接近原始的犹豫度情况,此外从偏好关系角度也提出基于一致性原则的NE方法。
然而上述几种方法都或多或少存在不足,乐观、悲观NE法仅仅利用最大、最小值来进行延拓,直观上必然会导致决策的失衡,这是显而易见的;0.5 NE法虽然是一种折中的态度,但是脱离了HFS原有的隶属度,在很多情况下是不切实际的;而ηNE法尽管根据η考虑了决策者的态度,但是其利用的NE是基于最大、最小值的态度,在最大、最小隶属度误差较大时,必然会导致错误决策。文献[34]认为延拓增加的元素应该是HFS中原有的元素,从HFS本质的角度讲这种方法是NE的初衷,但是在实施过程中并不事先知道究竟应该增加HFS中的哪个元素,特别是当HFS中元素较多时,如果任意增加会造成较大误差,因而风险性较大。基于一致性原则的NE方法,基本思想是利用一致性矩阵中元素增加的传递公式rij=rik+rkj-0.5实施的,但是上式本身就存在争议,一是传递公式右侧的减0.5值得商榷,二是当rik+rkj>1.5或rik+rkj<0.5时,显然是错误的,如果对任意的k,都满足rik+rkj>1.5或rik+rkj<0.5,则延拓增加的元素必然会大于1或小于0,此时此种延拓方法失效。
由于HFS中隶属度个数的统一问题在HFS距离、相似度和相关系数等度量计算、多属性决策领域起到关键作用。为此,本文试图解决HFS的隶属度数值个数统一问题,提出一种新的HFS隶属度NE方法,依次选取已有模糊集的隶属度可能值的均值作为一个新的延拓隶属度,直至所有模糊集数量相等为止,并基于有序加权平均(ordered weighted averaging,OWA)算子[35]归纳隶属度统一方法。最后将所提出的方法应用到多传感器电子侦察情报的多属性决策问题中。
1 HFS描述
本节主要引入HFS的定义,分析讨论HFS之间的性质和距离度量问题,为后续的研究提供理论基础。
1.1 HFS的定义
定义1[1-2]设论域X={x1,x2,…,xn},则X上的HFS被定义为
M={〈x,hM(x)〉|x∈X}
(1)
式中,hM(x)为[0,1]区间内的一系列不同取值,表示集合X中元素x对M的隶属度,为了方便,文中将HFS简写为hM(x)。
例如假设论域集合X={x1,x2,x3},hM(x1)={0.4,0.2},hM(x2)={0.5,0.4,0.3,0.6},hM(x3)={0.6,0.5,0.7},则X上的HFS为
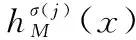
1.2 HFS的距离度量
假设M、N、O为X={x1,x2,…,xn}上的HFS,如果算子d(M,N)满足下列条件:
(1) 非负性:0≤d(M,N)≤1,当且仅当M=N时,d(M,N)=0;
(2) 对称性:d(M,N)=d(N,M);
(3) 三角不等式:d(M,N)≤d(M,O)+d(O,N)。
则称d(M,N)为M和N之间的距离度量。
文献[5-9]提出并详细分析了HFS的距离度量,这里仅提供4种常见的距离公式,并在最后的仿真分析进行应用,其他距离都是基于这4种距离的变形,可参考文献[5-9]。
(1) Hamming距离为
(2)
(2) Euclidean距离为
(3)
(3) 广义规范距离为
λ>0
(4)
(4) 广义规范Hausdorff距离为
λ>0
(5)
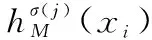
lxi=max{l(hM(xi)),l(hN(xi))}
(6)
2 基于Normative算子的HFS数值延拓方法
本节首先描述现有HFS隶属度NE方法存在的不足,其次基于一种合乎直观的思想提出基于Normative算子的HFS NE方法,并应用举例。
2.1 算法分析
一般情况下HFS中的隶属度可能值的数值个数不相等,这就导致无法进行HFS之间的距离等度量运算,通常通过NE的方法,将数量少的模糊集隶属度NE补齐和数量最多的模糊集一样长度。现有的NE补齐方法[5,15,21,32-34]主要是基于隶属度最大、最小进行NE的乐观、悲观法,0.5隶属度NE法、ηNE法和文献[34]中的方法,为了方便本文将上述前4种方法简记为乐观(optimistic,OP)法,悲观(pessimistic,PE)法,0.5法和η法。
引言中简要对上述方法的缺点进行了分析,OP法和PE法的主要缺点在于增加了决策的风险度,在获取的已知情报条件下,没有任何新息的加入,此时采用这两种方法进行决策都会增加风险度,所以其应用受到局限。
而0.5法从数值上看体现了一种折中的态度,但是其本质上是脱离原有决策隶属度基础的,与决策不存在逻辑关系,因而在很多情况下是不切实际的,必然会造成决策的更大风险,所以不建议采用。
最后η法在OP法和PE法的基础上采用一种η加权的偏好态度进行NE,具体做法为
(7)
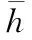
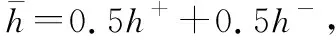
文献[34]中的方法认为增加元素为HFS中原有的元素,这种思想是延拓数值所寻求的,但是不清楚缺失的究竟是哪个元素,无法实现,只能减小风险去逼近这些缺失的元素。
所以为了克服上述几种HFS隶属度可能值的数值个数延拓方法的不足,提出一种基于Normative算子的HFS隶属度NE方法,Normative算子的物理意义是取平均计算,因此依次选取已有模糊集的隶属度可能值的均值作为一个新的延拓隶属度,直至所有模糊集数量相等为止。新算法的物理意义本身是在没有任何新息决策加入的情况下,基于现有的决策信息的一种稳妥决策,即采用现有的决策信息的均值作为新的隶属度进行延拓,这种方法相比之前的方法具有保均值性,更为稳定,能够更为完整地保留已知所有的决策信息,并且当决策信息改变时能够根据改变后的信息实时调整,保证了决策的有效性,不会像0.5法那样一成不变。同时承担的决策风险更小,直观上更符合决策者的思维,易于理解。
2.2 基于Normative算子的隶属度NE
直观上讲,在对2个数值决策犹豫不定时,往往会考虑一种折中的思想,即选取其均值作为决策结果,基于Normative算子的HFS隶属度NE方法正是基于这种思想实施的。
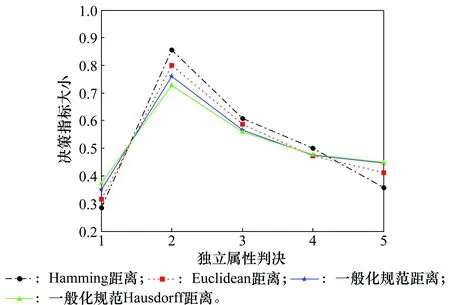
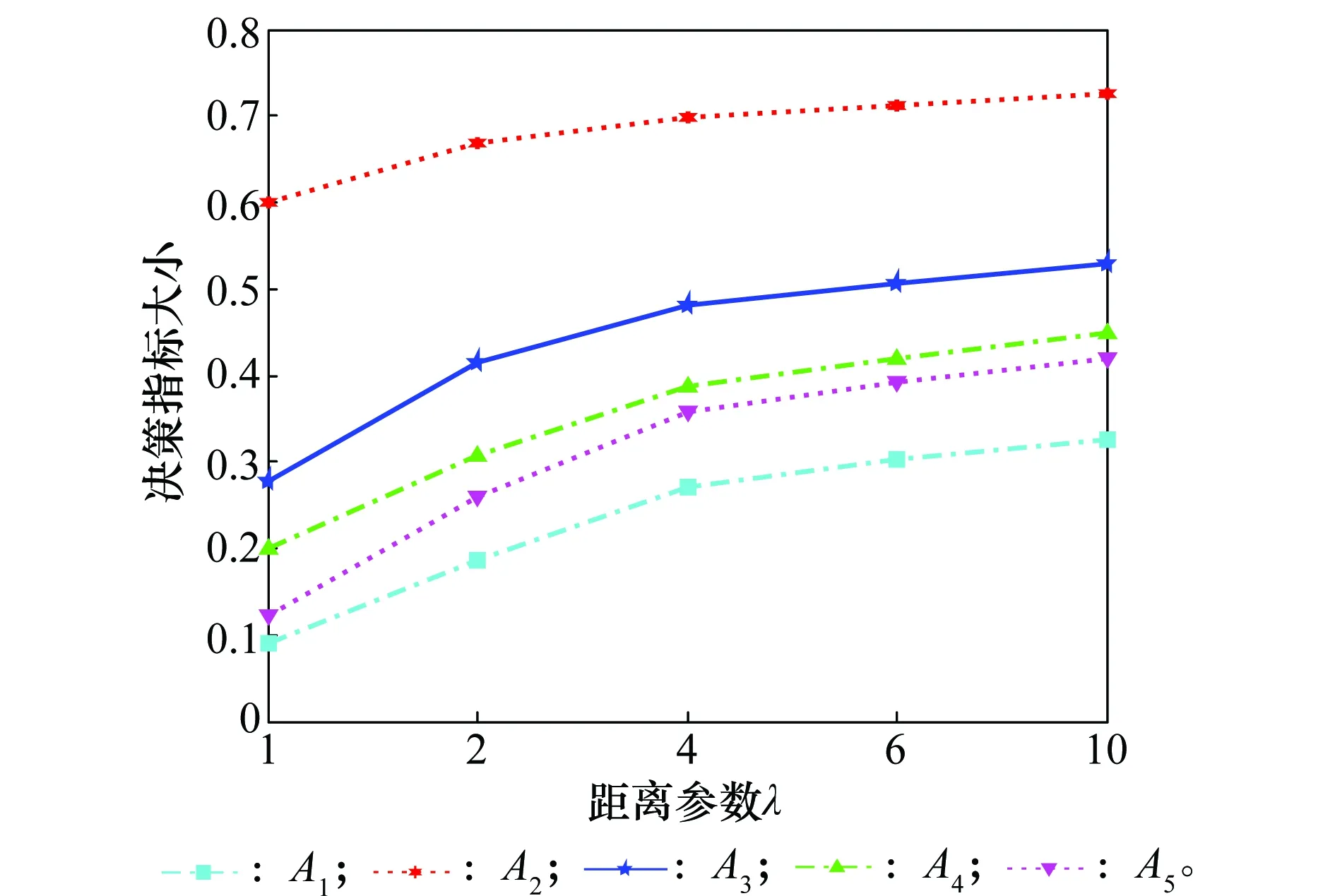
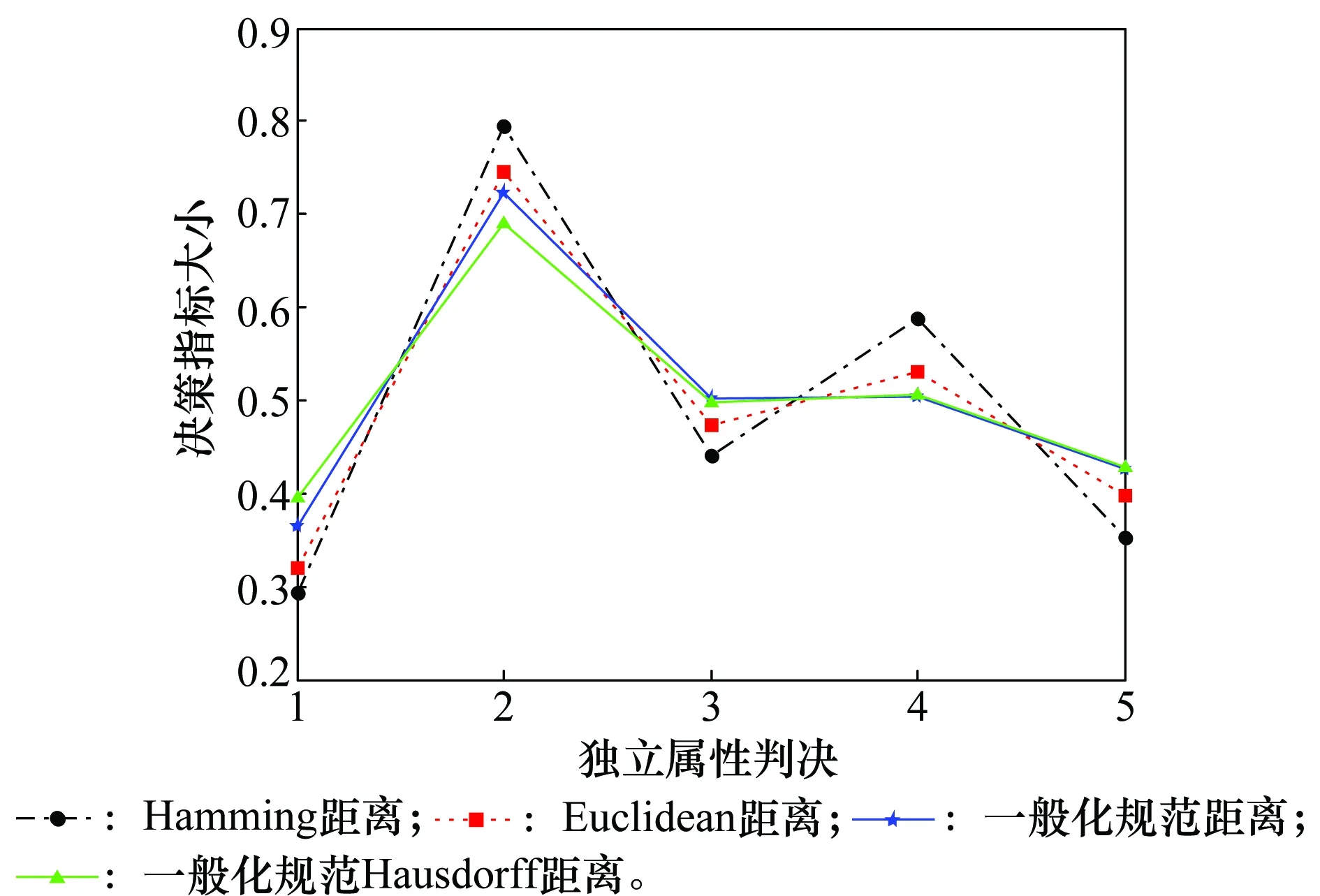
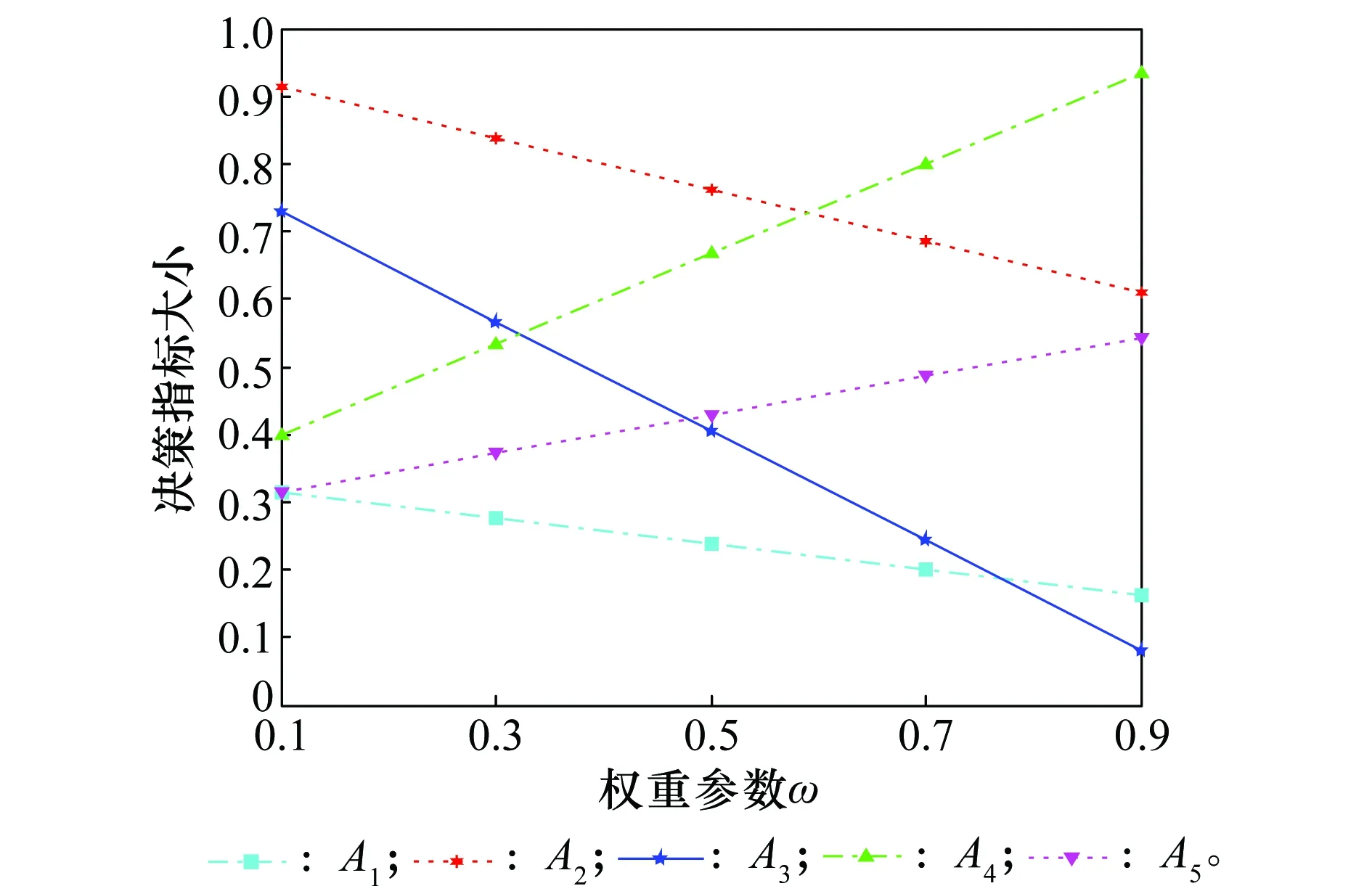
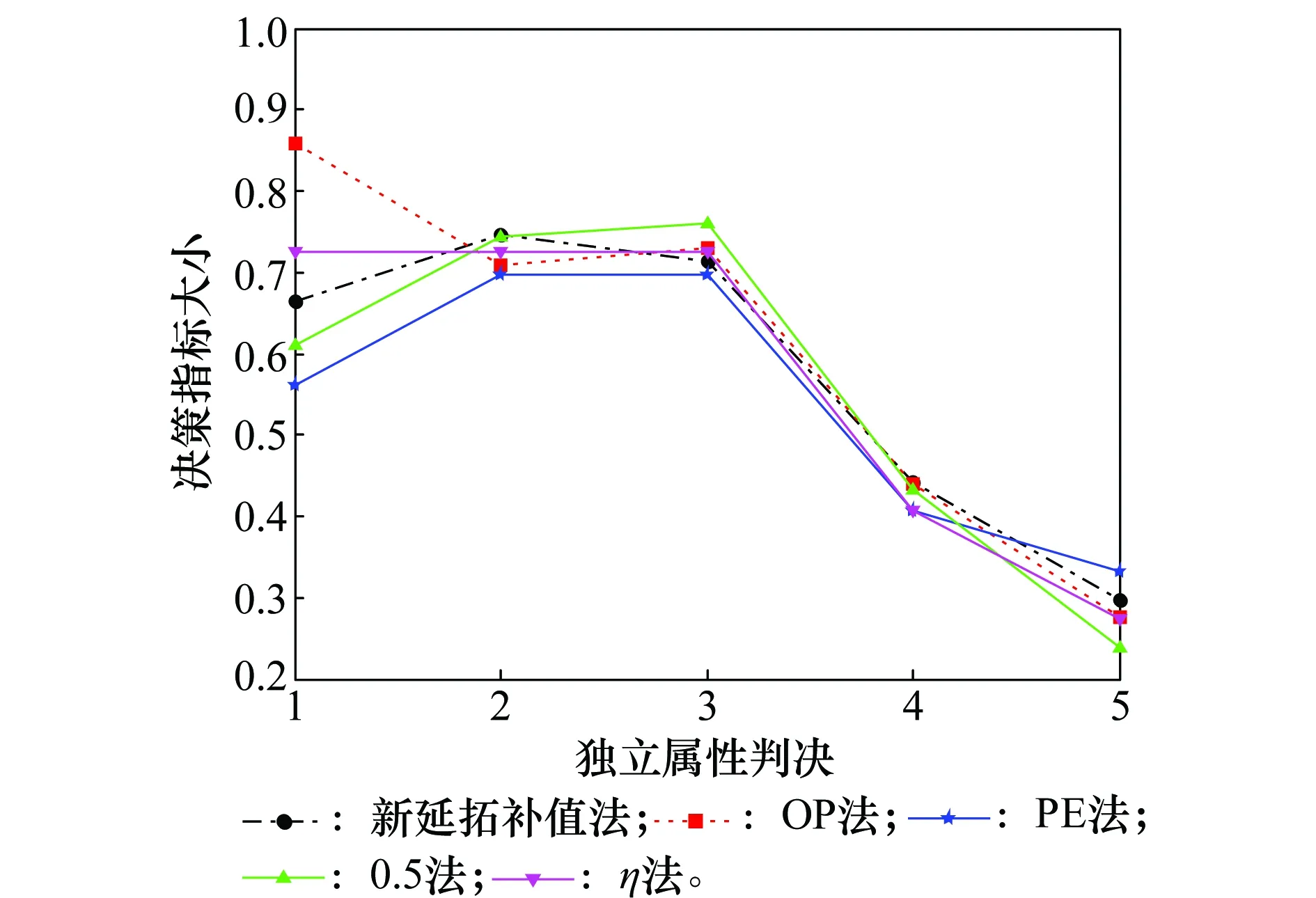
记HFShM(xi)={a1,a2,…,al(hM(xi))},hN(xi)={b1,b2,…,bl(hN(xi))},令l(hM(xi)) 基于Normative算子的隶属度NE方法描述为:依次计算现有决策信息HFS中隶属度的可能值的均值作为一个新的隶属度,并加入到隶属度集合中与原有的隶属度一起形成新的HFS,直至所有HFS中隶属度的数量相等,用数学语言表示为: 计算现有决策信息HFS中隶属度的可能值的均值为 (8) al(hM(xi))+1=al(hM(xi))+2=,…,= (9) 则NE后新的HFS为 (10) 例如,2个HFShN(xi)={0.6,0.7,0.5,0.4,0.1},hM(xi)={0.1,0.3,0.8},则需要对hM(xi)进行延拓补值,根据提出的新的HFS隶属度NE方法得到 则NE后 实际上,HFS的NE问题本质上是一类多对一映射问题,即在没有新息加入的条件下,利用已有的隶属度更新新的隶属度。为此本文基于OWA算子的思想,首次对HFS的隶属度NE方法进行归纳。 假设HFSh(x)={γ1,γ2,…,γi,…,γn},现在需要将其隶属度个数由n延拓至m,n 首先记向量为 (11) 其次,计算h(x)的OWA算子为 k=1,2,…,m-n,j=1,2,…,n (12) OP算子:w=(1,0,…,0); PE算子:w=(0,0,…,1); Hurwicz算子:w=(η,0,…,(1-η)); 上述算子分别表示前文中所述的OP法、PE法,η法和本文新提出的折中方法。向量算子的不同,NE的方法随之改变,式(12)很好地归纳了HFS的NE方法。例如利用式(12)对h(x)={0.1,0.3,0.8}进行隶属度延拓使得隶属度个数达到5,首先进行降序排列得到{0.8,0.3,0.1},再利用上述4种算子(1,0,0),(0,0,1),(η,0,(1-η))和(1/3,1/3,1/3)分别进行延拓,取η=0.5,则分别得到以下结果{0.8,0.8,0.8,0.3, 0.1},{0.8,0.3,0.1,0.1,0.1},{0.8,0.45,0.45,0.3,0.1},和{0.8,0.4,0.4,0.3,0.1}。 本节利用HFS的隶属度来描述电子侦察情报各传感器上报的带有不确定性的独立属性判决,解决因不确定性造成的模糊属性决策问题。 记各传感器独立属性判决为Ai(i=1,2,…,n),假设每类判决具有P={p1,p2,…,pj,…,pm}类属性(属性判决的属性不一致,类别不完全相同依然适用),令属性判决Ai在属性pj上的独立犹豫模糊判决为hAi(pj),则记属性判决Ai在属性集P上的HFS为 Ai={〈pj,hAi(pj)〉|pj∈P} (13) 式中,hAi(pj)由一组[0,1]区间内的可能值组成,则所有传感器上报的带有不确定性的独立属性判决A可以用HFS表示为 A= (14) 式中,1≤i≤n,1≤j≤m。通过式(14)就可以将各传感器带有不确定性的独立决策判决用HFS的形式描述,进一步只需根据式(14)进行HFS多属性决策就可以实现对电子侦察情报的判定。 由于属性判定不是本文研究的重点,所以暂不提供一种新的决策判定方法,也不讨论属性的效益型、成本型及最优属性权重的规划问题,而基于现有的与理想状况相似的偏好排序技术(technique for order preferences by similarity to ideal solution,TOPSIS[36-37])方法进行决策判定,仅就属性权重对决策的影响和各种距离的效果进行分析,来解决HFS的多属性决策问题,这并不影响本文方法的适用性。 (15) 之后基于TOPSIS法按属性值遍历,求得各判决属性的正负理想解为 (16) (17) (18) (19) 式中,i=1,2,…,n,lpj为隶属度NE后新的HFS中隶属度的数量。 定义决策判定指标为 (20) 则根据ξi的大小排序即可进行决策判定,由于决策判定指标ξi的物理意义为决策方案与正负理想方案之间差异的一种特殊比值,显然正确的决策方案应该越靠近正理想方案,因此决策判定不应当简单地按照ξi的大小排序选取最大的作为最终的决策结果,而需要在决策判定时对ξi进一步限定。为此,这里对传统的TOPSIS法进行了改进,基于决策指标的物理意义,增加决策门限ε,0.5<ε≤1,本文称之为TOPSIS-ε法,如果 (21) 判定ξimax对应的决策方案为决策结果,如果有 (22) 则决策矛盾,无法给出正确决策方案,需要重新决策。 上述方法是在没考虑各属性重要性的情况下得到的,但考虑到各属性在决策中的重要性往往不同,所以在决策过程中应考虑属性权重的影响。记各属性权重向量为 (23) (24) (25) 则加权后的融合决策判定指标为 (26) 同样根据改进后的TOPSIS-ε法进行决策判定。 基于TOPSIS的电子侦察情报犹豫模糊多属性决策步骤如下: 步骤1将各传感器上报的独立属性判决用HFS表示,形成HFS属性判决矩阵A; 步骤3基于TOPSIS法按属性值遍历形成正负理想解hZj(pj)和hFj(pj); 步骤5基于正负理想距离计算决策判定指标ξi; 步骤6根据ξi大小排序,若满足TOPSIS-ε法,则判定ξi大的对应的决策方案为决策结果。 本节将所提出的基于Normative算子的HFS NE方法应用到电子侦察情报的多属性决策中。电子侦察情报处理中,我方Radar、电子支援措施(electronic support measures, ESM)、红外等传感器量测到的敌方载频、脉冲重频、脉宽、功率等多个属性信息,通过这些属性信息对敌方的机载平台进行多属性决策判定其属于哪一类,最后在融合中心进行融合判定。而量测过程中往往受到敌方干扰,造成量测信息的不确定性,因此通过HFS描述这些独立属性判决。假设各传感器上报给融合中心5类独立属性判决,分别记为A1、A2、A3、A4、A5,每类属性判决具有4类属性,分别记为p1、p2、p3、p4,融合中心根据4类属性对具有不确定性的5类属性判决进行多属性融合判定,判定敌方的机载平台类型。5类独立属性判决以HFS的形式表示,如表1所示。 表1 HFS独立属性判决表 首先基于新的HFS NE方法对表1中的隶属度进行NE,并按降序排列,得到延拓后的HFS判决如表2所示。 表2 NE后的HFS独立属性判决表 按照式(16)和式(17)计算NE后的HFS各属性判决的正负理想解分别为 hZ(p1)={0.8,0.75,0.75,0.7} hZ(p2)={0.8,0.7,0.7,0.6} hZ(p3)={0.6,0.55,0.55,0.5} hZ(p4)={0.9,0.8,0.8,0.7} hF(p1)={0.4,0.3,0.3,0.2} hF(p2)={0.4,0.35,0.35,0.3} hF(p3)={0.4,0.3,0.3,0.2} hF(p4)={0.5,0.45,0.45,0.4} 则所有HFS属性判决的正负理想解分别为 Z= F= 按照距离式(18)和式(19)计算各HFS属性判决与正负理想解Z、F之间的正负理想距离分别为 {0.250 0,0.050 0,0.137 5,0.175 0,0.225 0} 最后按照式(20)计算融合决策判定指标分别为 ξ={0.2857,0.8571,0.6071,0.5000,0.3571} 根据融合决策判定指标得知融合后的属性判决排序为 A2>A3>A4>A5>A1 所以经融合中心多属性决策,判定第2类属性判决为决策结果,即判定敌方机载平台为A2。 对比分析采用4组对比试验,一是HFS不同距离的对比计算,二是讨论距离参数λ对决策结果的影响,三是讨论属性权重对决策结果的影响,最后重点对比新的NE方法与已有4种延拓方法的应用效果。 (1) 距离计算对比 第1.2节提供了4种距离计算方法,第4.2节仅以Hamming距离为例进行计算,本节用给出的4种距离计算方法分别计算HFS属性判决与正负理想解之间的距离,其中一般化距离中以λ=5为例进行计算,关于距离参数λ的影响在下一节重点分析,经计算得到4种距离计算的决策对比效果如图1所示。 图1 4种距离计算的融合决策对比图Fig.1 Fusion decision contrast diagram of 4 kinds of distance calculation 4种距离计算后的决策指标分别为 ξ1={0.285 7,0.857 1,0.607 1,0.500 0,0.357 1} ξ2={0.314 9,0.801 0,0.586 8,0.471 5,0.411 4} ξ3={0.349 9,0.760 1,0.565 0,0.474 0,0.446 4} ξ4={0.374 2,0.727 0,0.558 2,0.476 0,0.449 5} 由图1和指标计算得知,融合后的属性判决排序均为 A2>A3>A4>A5>A1 通过4种距离计算得到经融合中心融合后的判别结果是一致的,均为第2类属性判决,即判定敌方机载平台为A2,所以在本文应用算例中没有特殊要求的情况下,采用任一种距离计算都是合理的。 (2) 距离参数计算对比 本节讨论一般化规范距离中不同的距离参数λ对决策结果的影响,理论上讲λ的取值为0到正无穷,但是距离计算中没有任何一种距离将λ的取值设定的太大,并且λ太大也是无意义的,只需采用部分取值得到距离随λ参数变化的趋势即可,因此λ值设为1、2、4、6、10,进行分析距离参数λ对决策结果的影响。经计算得到的决策指标随距离参数λ的变化对比图如图2所示。 图2 决策指标随距离参数变化图Fig.2 Diagram of decision indexes with distance parameters 由图2得到,不同距离参数λ计算后的属性判决排序均为 A2>A3>A4>A5>A1 尽管距离参数λ变化,但是决策结果并没有随着距离参数λ的变化而改变,始终为A2,而且各属性决策指标大小随着距离参数的变化趋势是一致的,都随着距离参数的增加而递增至比较平稳的数值,且变化幅度相对稳定。所以可以将距离参数作为决策的一种态度,其在一定范围内的改变并不会影响决策结果的改变,在合理的情况下,采用任一种距离参数进行计算都是允许的。 (3) 加权计算对比 上述两节的计算结果是在没有考虑权重的条件下得到的,但在实际决策过程中,属性权重对决策的作用不容忽视,第3.2节考虑到各属性在决策中的重要性往往不同,提供了加权计算方法,为此本节讨论属性权重对决策结果的影响。将4类属性权重分别设为0.1、0.3、0.2、0.4,再按照第3.3节的算法步骤计算,得到的决策指标对比图如图3所示。 由图3得知,4种距离计算后得到的决策指标排序均为 A2>A4>A3>A5>A1 通过图3和图1对比得知,在考虑权重的情况下通过4种距离计算得到经融合中心融合后的决策判别与不考虑权重时的计算结果排序有所不同,所以说权重的变化对计算结果有影响,为进一步讨论权重的问题,假设属性4的权重从0.1按步长0.2变化到0.9,其余属性权重平均,以Hamming距离为例计算进行距离计算,得到的决策指标随权重的变化图如图4所示。 图3 不同权值条件下的决策对比图Fig.3 Fusion decision contrast diagram of different weights conditions 图4 决策指标随权重的变化图Fig.4 Diagram of decision indexes with different weights 由图4得知,各属性决策指标大小随着权重参数的变化而变化,其中属性判决A1、A2、A3的决策指标随着权重参数的增加而减小,而A4、A5的决策指标随着权重参数的增加而增大,并且当属性4的权重在0.6附近时,决策结果发生变化,由原来的A2变为A4,所以说属性权重在进行多属性融合决策时占有十分重要的作用,在决策前应充分考虑权重的分配,以便得到更合理的决策结果。 (4) NE方法对比 第2节提出了新的HFS NE方法,并分析了现有方法的局限性,本节为了更直观地对比新方法和已有的OP法、PE法、0.5法和η法4种延拓补值方法的效果,构造了多属性决策对比试验,其中采集的试验数据如表3所示。 表3 HFS独立属性判决表 分别按照本文所提出的新的HFS NE方法和已有的OP法、PE法、0.5法和η法5种NE方法对表3中属性判决进行NE,并经第3.3节的多属性决策步骤进行多属性决策判定(距离计算采用汉明距离计算,其他距离可类似计算,为了与新方法的折中思想对比明显η法计算时取η=0.5进行计算,其他η取值可类似计算),得到决策效果对比如图5所示。 图5 不同延拓方法计算的融合决策对比图Fig.5 Fusion decision contrast diagram of different extending methods 经5种方法计算后的决策指标分别为 ξ1={0.663 9,0.746 2,0.713 3,0.443 1,0.297 7} ξ2={0.858 1,0.709 5,0.729 7,0.439 2,0.277 0} ξ3={0.561 7,0.697 5,0.697 5,0.407 4,0.333 3} ξ4={0.610 6,0.743 4,0.761 1,0.433 6,0.238 9} ξ5={0.725 9,0.725 9,0.725 9,0.407 4,0.274 1} 由图5和指标计算得知,融合后的属性判决排序结果为 新方法:A2>A3>A1>A4>A5 OP法:A1>A3>A2>A4>A5 PE法:A2=A3>A1>A4>A5 0.5法:A3>A2>A1>A4>A5 η法:A1=A2=A3>A4>A5 通过属性判决结果得到,经5种方法计算后得到5种不同的计算结果,新的NE方法得到的决策结果为A2,OP法得到的决策结果为A1,0.5法得到的决策结果为A3,而PE法和η法得到的决策结果分别有多个,PE法为A2和A3,η法为A1、A2和A3,实际中出现多个决策结果应当归属于无效决策,因此在本试验中PE法和η法没有决策结果。对比5种方法的计算结果,对其进行数据分析得知。OP法的计算结果之所以为A1是因为在属性判决1中,每个犹豫模糊属性隶属度中都存在0.8、0.9等较大的隶属度,而OP法正是通过这些最大值进行NE而忽略了其余隶属度的作用,导致决策结果错误地判定为A1。0.5法判决结果为A3的原因在于其脱离隶属度本身,无论原有隶属度为何值其都会以0.5延拓,A3与正确结果A2之间本来差异就不是很明显,通过0.5延拓,正好将A3中隶属度在0.5以下的数值忽略,而导致其计算结果高于A2,因而属于错误决策。PE法则将隶属度的最小值的作用放大,特别是在需要延拓个数较多的HFS中,这样导致其余原有大部分隶属度的作用弱化,造成了较大误差,因而导致A2和A3的计算结果相同。η法的缺点在于只考虑了最大最小值,这样导致最值相近的一些决策的结果就很接近,特别是当隶属度数值需要延拓个数较多的时候,最值之间内部的隶属度实际上占有决定性作用,η法往往忽略了起作用,因而导致A1、A2和A3的计算结果相同。而本文提出的新的HFS NE方法考虑了所有HFS隶属度的共同作用,得到了正确的决策结果A2。新方法避免了前4种方法的共同特点:仅利用局部隶属度NE;并且通过隶属度平均化,能够克服因量测误差造成错误决策而产生少数偏离正常隶属度的突变隶属度的情况,具有更强的稳定性,决策风险更小,从直观上更符合决策的直觉思维,易于理解。 针对HFS中隶属度数值个数不统一导致其度量方法不能直接运算的问题,首先分析了现有HFS隶属度NE方法,并分别指出其局限性,之后基于折中的思想提出了基于Normative算子的HFS隶属度NE方法,并成功应用于多传感器电子侦察情报融合决策中,结合现有的TOPSIS方法并将其拓展为TOPSIS-ε法进行决策判定,得到了满意的决策结果。同时通过不同的HFS仿真试验,讨论了4种距离计算,距离参数、属性权重对决策结果的影响,得到在没有特殊要求时,不同距离计算、距离参数并不影响融合结果,而属性权重的变化可能会对决策结果产生影响,决策时应充分考虑权重赋值。最后重点对比了所提出新的HFS隶属度NE方法与现有的4种NE方法的应用性,在本文算例中只有新方法得到了正确的决策结果,其余方法均因其局限性而导致错误决策,验证了新NE方法的准确性和稳定性。本文方法亦可以拓展到区间HFS领域,进行进一步的研究及应用。 参考文献: [1] MARDANI A, JUSOH A, ZAVADSKAS E K. Fuzzy multiple criteria decision-making techniques and applications-Two decades review from 1994 to 2014[J]. Expert Systems with Applications, 2015, 42(8):4126-4148. [2] LIU W S, LIAO H C. A bibliometric analysis of fuzzy decision research during 1970-2015[J]. International Journal of Fuzzy Systems, 2017, 19(1): 1-14. [3] BLANCO-MESA F, MERIGO J M, GIL-LAFUENTE A M. Fuzzy decision making: A bibliometric-based review[J]. Journal of Intelligent & Fuzzy Systems, 2017, 32(3):2033-2050. [4] TORRA V. Hesitant fuzzy sets[J].International Journal of Intelligent Systems, 2010, 25(6):529-539 [5] XU Z S, XIA M M. Distance and similarity measures for hesitant fuzzy sets[J]. Information Sciences, 2011, 181(11):2128-2138. [6] XU Z S, XIA M M. On distance and correlation measures of hesitant fuzzy information[J]. International Journal of Intelligent Systems, 2011, 26(5):410-425. [7] LI D Q, ZENG W Y, ZHAO Y B. Note on distance measure of hesitant fuzzy sets[J]. Information Sciences, 2015, 321:103-115. [8] LI D Q, ZENG W Y, LI J H. New distance and similarity measures on hesitant fuzzy sets and their applications in multiple criteria decision making[J]. Engineering Applications of Artificial Intelligence, 2015, 40: 11-16. [9] LIU Y, LIU J, HONG Z Y. A multiple attribute decision making approach based on new similarity measures of interval-valued hesitant fuzzy sets[J]. International Journal of Computational Intelligence Systems, 2018, 11(1): 15-32. [10] XIA M M, XU Z S. Hesitant fuzzy information aggregation in decision making[J].International Journal of Approximate Reasoning, 2011, 52(3): 395-407. [11] XIA M M, XU Z S, CHEN N. Some hesitant fuzzy fuzzy aggregation operators with their application in group decision making[J].Group Decision and Negotiation, 2013, 22(2): 259-279. [12] ZHANG S, XU Z S, HE Y. Operations and integrations of probabilistic hesitant fuzzy information in decision making[J]. Information Fusion, 2017, 38: 1-11. [13] LIAO H C, XU Z S. Subtraction and division operations over hesitant fuzzy sets[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(1): 65-72. [14] LIAO H C, XU Z S, ZENG X J. Novel correlation coefficients between hesitant fuzzy sets and their application in decision making[J].Knowledge-Based Systems,2015,82(C):115-127. [15] LIAO H C, XU Z S, XIA M M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making[J]. International Journal of Information Technology & Decision Making, 2014, 13(1): 47-76. [17] WU Z B, XU J P. A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters[J]. Information Fusion, 2018, 41:217-231. [18] ZHANG Z M. Hesitant fuzzy multi-criteria group decision making with unknown weight information[J]. International Journal of Fuzzy Systems, 2017, 19(3): 615-636. [19] ZHANG Z M. A framework of group decision making with hesitant fuzzy preference relations based on multiplicative consistency[J].International Journal of Fuzzy Systems,2017,19(4): 982-996. [20] WEI G W, ALSAADI F E, HAYAT T, et al. A linear assignment method for multiple criteria decision analysis with hesitant fuzzy sets based on fuzzy measure[J]. International Journal of Fuzzy Systems, 2017, 19(3): 607-614. [21] XU Z S, ZHANG X L. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information[J]. Knowledge-Based Systems, 2013, 52(6): 53-64. [22] ZHANG X L, XU Z S. Hesitant fuzzy agglomerative hierarchical clustering algorithms[J]. International Journal of Systems Science, 2015, 46(3):562-576. [23] CHEN N, XU Z S, XIA M M. Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J]. Applied Mathematical Modelling, 2013, 37(4): 2197-2211. [24] YANG X, XU Z S, LIAO H C. Correlation coefficients of hesitant multiplicative sets and their applications in decision making and clustering analysis[J]. Applied Soft Computing, 2017, 61: 935-946. [25] LI C Q, ZHAO H, XU Z S. Kernel C-means clustering algorithms for hesitant fuzzy information in decision making[J]. International Journal of Fuzzy Systems, 2018, 20(1): 141-154. [26] GUAN X, SUN G D, YI X, et al. Grey relational analysis for hesitant fuzzy sets and its applications to multi-attribute decision making[J]. Mathematical Problems in Engineering, 2018, Article ID: 7436054. [27] SUN G D, GUAN X, YI X, et al. Grey relational analysis between hesitant fuzzy sets with applications to pattern recognition[J]. Expert Systems with Applications, 2018, 92: 521-532. [28] EBRAHIMPOUR M K, EFTEKHARI M. Ensemble of feature selection methods: a hesitant fuzzy sets approach[J]. Applied Soft Computing, 2017, 50: 300-312. [29] RODRíGUEZ R M, MARTíNEZ L, HERRERA F. Hesitant fuzzy linguistic term sets for decision making[J]. IEEE Trans.on fuzzy Systems, 2012, 20(1): 109-119. [30] LIAO H C, XU Z S, ZENG X J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making[J]. IEEE Trans.on fuzzy Systems, 2015, 23(5):1343-1355. [31] LIAO H C, XU Z S, HERRERA-VIEDMA E, et al. Hesitant fuzzy linguistic term set and its application in decision making: a state-of-the-art survey[J]. International Journal of Fuzzy Systems, DOI: 10.1007/s40815-017-0432-9. [32] ZHU B, Xu Z S, XU J P. Deriving a ranking from hesitant fuzzy preference relations under group decision making[J]. IEEE Trans.on Cybernetics, 2014, 44(8): 1328-1337. [33] ZHU B, XU Z S. Consistency measures for hesitant fuzzy linguistic preference relations[J]. IEEE Trans.on Fuzzy Systems, 2014, 22(1): 35-45. [34] XU Y J, CABRERIZO F J, HERRERA-VIEDMA E. A consensus model for hesitant fuzzy preference relations and its application in water resource management[J]. Applied Soft Computing, 2017, 58: 265-284. [35] YAGER R R. On ordered weighted averaging aggregation operators in multi-criteria decision making[J]. IEEE Trans.on Systems, Man, and Cybernetics, 1988, 18(1): 183-190. [36] ZYOUD S H, HANUSCH D F. A bibliometric-based survey on AHP and TOPSIS techniques[J]. Expert Systems with Applications, 2017, 78: 158-181. [37] SUN G D, GUAN X, YI X, et al. An innovative TOPSIS approach based on hesitant fuzzy correlation coefficient and its applications[J]. Applied Soft Computing, 2018, 68: 249-267.
2.3 基于OWA算子的HFS隶属度统一
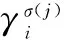
3 基于TOPSIS的电子侦察情报多属性决策判定
3.1 犹豫模糊属性表示
3.2 犹豫模糊多属性决策判定
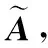
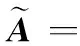
3.3 算法步骤
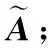
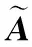
4 电子侦察情报多属性决策应用
4.1 仿真环境

4.2 仿真实验

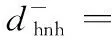
4.3 对比分析

5 结 语

