基于序优化的多传感器协同雷达辐射控制

李 波, 李卿莹, 高晓光, 张春燕

(西北工业大学电子信息学院, 陕西 西安 710072)

0 引 言

随着多传感器管理(multi-sensor management, MSM)技术的不断发展与进步[1-2]及飞机隐身性能和反隐身技术的不断提高[3-4],对多传感器协同(multi-sensor collaboration, MSC)探测[5-6]的研究已成为热点。多传感器系统(multi-sensor system,MSS)由主动传感器和被动传感器2部分构成,且系统内各传感器有着不同的作用范围和功能。主动传感器即为机载雷达,可以同时探测目标的角度和距离信息;被动传感器只能获取目标的角度信息,如机载红外搜索跟踪(infrared search and track, IRST)系统、电子支援措施(electronic support measure, ESM)等,对各传感器探测到的目标信息进行融合,能够有效提升载机探测、跟踪目标的能力[7]。但是,雷达开机会向外界辐射电磁波,容易被敌方侦察机侦察或干扰,因此应尽可能地减少雷达的开机辐射时间[8]。采用雷达与被动传感器协同探测,在保证跟踪精度的条件下,尽可能减少雷达的开机时间,不仅可以提高飞机的探测和跟踪能力,还可以提高飞机的隐蔽性。

20世纪70年代,文献[9]在传感器管理中采用线性规划的方法进行传感器-目标分配。到了90年代,通信与传感器技术大力发展,但直接对信息进行融合的传统方法因平台运动、分布位置、通信带宽、计算能力和能量等的限制而无法有效实施。90年代初期,SM的研究在国外逐渐成为热潮。文献[10-11]在传感器管理(sensor management,SM)中应用了信息论(information theory, IT)中熵的概念。国外对于MSM算法的研究,应用了许多领域的技术[12-16]。

国内对SM算法的研究起步比较晚。文献[17]通过分析作战效能论证了MSC下的雷达猝发探测技术在未来空战中具有可实施性;文献[18]在辐射限制下对有/无源传感器进行管理,协同目标跟踪;文献[19]在目标跟踪过程中通过比较距离测量熵与距离估计信息熵对雷达开关机进行实时控制;文献[20]提出了通过比较跟踪的预测协方差、预定门限来控制雷达辐射的方法;文献[21]则对在雷达辐射控制(radar radiation control, RRC)基础上所构建的异类MSS综合与管理方法进行了研究；文献[19-21]都采用雷达实时辐射控制方式但并未对辐射控制因子进行优化求解；文献[22]研究设计了主被动雷达协同探测跟踪模式,并提出改进的自适应交互式多模型不敏滤波算法。近年来,国内关于MSC跟踪的研究虽有一定突破性进展和成果[23-24],但在其理论创新与应用实践方面仍然还有许多关键技术问题需要深入研究和解决。

本文提出雷达混合辐射控制(radar mixed radiation control, RMRC)方式,并找出符合要求的雷达辐射周期Tc和辐射控制因子k最优的组合,使得MSC探测跟踪过程中在保证跟踪精度的同时尽量减小雷达开关机次数以提高作战飞机电磁隐身性能。在跟踪过程中,采用交互式多模型(interaction multiple model,IMM)算法[25-26]实现对单目标的跟踪,利用扩展卡尔曼滤波(extend Kalman filter,EKF)算法[25]对跟踪结果进行滤波,建立了MSC下RRC的参数优化模型。在等间隔控制、实时控制和混合控制下分别进行仿真,得出结论。

1 MSC下RRC方式

1.1 等间隔控制方式

雷达的等间隔辐射是最简单的辐射控制方式。在该控制方式下,雷达采用固定的辐射周期Tc进行辐射,且辐射周期是离线计算的。其基本思想为:在确定的作战条件下,根据已知的传感器量测误差及预测所需的跟踪精度,考虑不同的目标类型、目标距离、战斗需要等因素,离线计算出针对某种目标的雷达等间隔辐射周期Tc。该控制方式比较简单,实现也比较容易。

1.2 实时控制方式

由于雷达辐射的等间隔控制方式不仅需要离线计算出辐射周期Tc,而且需要对目标类型做出判断,因此不确定性较大。而且在这种辐射周期固定的工作方式下,雷达可能在被动传感器单独对目标跟踪效果很好的情况下开机工作,此时雷达对跟踪效果的帮助较小,反而向外辐射电磁波,这样不仅造成了辐射资源的浪费,还增加了我方被敌方侦察跟踪的风险;反之,雷达可能在被动传感器对目标跟踪效果较差的情况下不开机,这样就不能满足对目标的跟踪要求,严重时还可能造成目标丢失。因此提出一种比较灵活的实时控制方式,雷达是否发射电磁波主要由系统对目标跟踪的实时效果进行评估决定。该方法是通过比较目标滤波残差范数d(k)与门限从而实现雷达开关机的实时控制。根据滤波理论,d(k)服从自由度为m(m为观测维数)的卡方分布,由此通过滤波残差控制雷达开关机就相当于一个假设检验问题,即检验d(k)是否位于以m为中心的置信区间(m-kσd(k),m+kσd(k))内。k为决定置信区间长度的系数,称其为辐射控制因子。

1.3 混合控制方式

由于雷达辐射的实时控制方式中雷达的开机次数过于频繁,易被敌方探测跟踪,不利于我机的隐身性。因此提出一种混合控制方式,将等间隔控制和实时控制结合起来,即雷达采用固定的辐射周期Tc,同时利用目标残差范数来确定雷达是否开机。这样既可以避免雷达以固定辐射周期探测带来的灵活性差和目标丢失等问题,同时又避免了每次量测更新时目标残差范数计算量大及雷达开机次数过多的缺点。在混合控制方式下,要避免丢失目标,应尽量使雷达辐射周期小。MSC下雷达混合控制方式流程如图1所示。

图1 混合控制流程图Fig.1 Flow chart of hybrid control

2 MSC下RRC参数优化模型

2.1 基于IMM-EKF的MSFT算法

本文的MSS采用匀速直线运动、匀速左转弯和匀速右转弯3种模型对目标进行协同跟踪,交互式多模型-扩展卡尔曼滤波(interaction multiple model-extend Kalman filter,IMM-EKF)算法对这3种模型进行交互跟踪。

假设目标运动的状态方程为

xt+1=Φtxt+wt

(1)

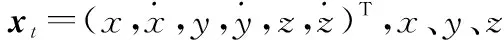
在匀速运动(constant velocity, CV)模型假设下有

(2)

在匀速转弯(constant turn, CT)模型假设下有

(7)

观测方程为

zt=h[xt]+vt

(8)

式中,T为传感器的采样周期;ω为匀速转弯的角速度;zt为观测向量;vt为服从高斯分布的白噪声,即:vt～N(0,Rt),Rt为观测噪声协方差矩阵。wt和vt相互独立,系统的观测方程为非线性方程。针对不同的传感器,量测的量不同,故观测方程有不同的形式,具体如下:

主动传感器可以测量目标的距离r、方位角θ和俯仰角φ,即

(9)

被动传感器只能测量目标的方位角θ和俯仰角φ,即

(10)

基于IMM-EKF的多传感器融合跟踪(multi-sensor fusion tracing,MSFT)算法如图2所示。

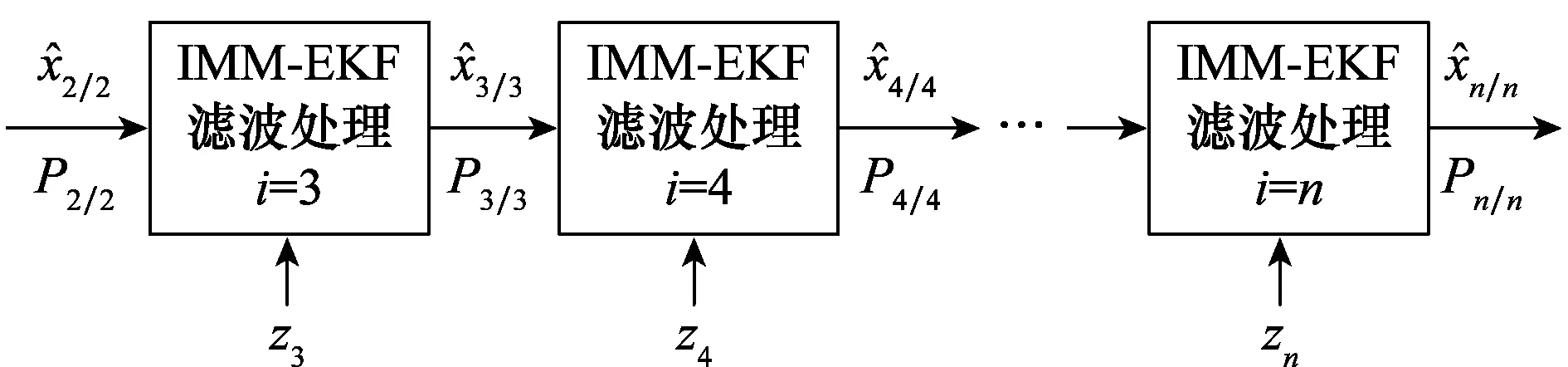
图2 基于IMM-EKF的MSFT算法Fig.2 MSFT algorithm based on IMM-EKF

2.2 RMRC参数优化模型

RMRC就是要在保证对目标跟踪精度的条件下,尽可能地减少雷达开机次数。在RMRC策略下,雷达以一定的辐射控制周期Tc和辐射控制因子k共同完成雷达的开关机控制过程。在MSC对目标进行跟踪过程中,辐射周期Tc越小,量测信息越充分,目标跟踪精度越高;辐射周期Tc越大,雷达工作次数越少,目标跟踪精度越低;辐射控制因子k越小,置信区间越大,雷达开机次数越多,目标跟踪精度越高;辐射控制因子k越大,置信区间越小,雷达开机次数越少,目标跟踪精度越低,即雷达辐射周期Tc大小和辐射控制因子k大小将直接影响到对目标的协同跟踪效果。

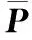
(11)

(12)

式中,Pj为第j次滤波得到的状态误差协方差矩阵;Ns为滤波次数,由跟踪时间和采样周期共同决定,即Ns=Ttrack/Ts。

基于MSC的RRC问题,就是确定出最佳的参数组合,使得MSC目标跟踪精度尽可能接近期望跟踪精度,即

(13)

上述优化问题保证了目标跟踪精度在高于期望跟踪精度的前提下,尽可能接近期望跟踪精度,这样能够在保证跟踪精度的同时,尽量减少雷达开机时间,提升电磁隐身性能。式(13)中的目标函数和约束条件都不能显式给出,要借助IMM-EKF的迭代仿真计算得出。因此,上述优化问题可以采用基于仿真的优化方法进行求解。

3 基于OO的RRC参数优化模型求解

对于单目标复杂优化问题,通常其解空间具有复杂的结构,且随着问题规模增大,其解集大小也会呈指数级增大。因此,需要大量的时间进行仿真计算,且常常得不到满意的解。

1992年,文献[27-31]最先提出了序优化(ordinal optimization, OO)理论。作为一种求解单目标复杂优化问题的有效工具,其基本思想包含排序比较和目标软化,实际工程中的问题往往比较复杂、求解规模较大且解空间结构比较复杂,而OO理论方法在解决这类复杂问题时具有更强的能力,可以有效提高计算效率。

一般地,OO理论将单目标优化问题分为5种类型:Neutral型、Bell型、Steep型、U-shaped型和Flat型,分别对应的有序性能曲线(ordered performance curve,OPC)[31]如图3所示。根据问题所对应的OPC可以确定优化问题的类型,就可以根据相应的原则求解足够好的优化方案。

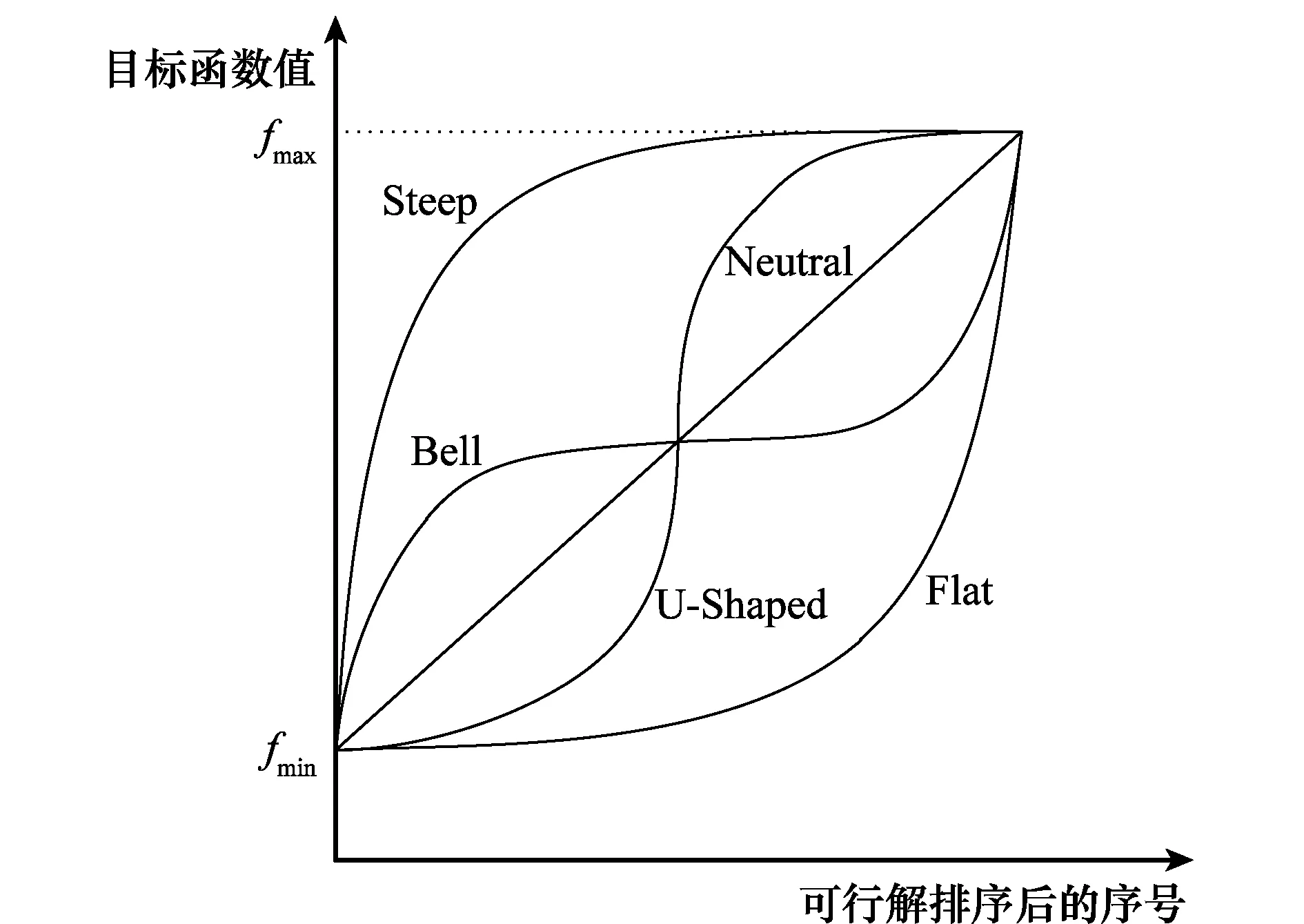
图3 OO OPCFig.3 OPC of OO

RRC参数优选的OO求解步骤如图4所示。

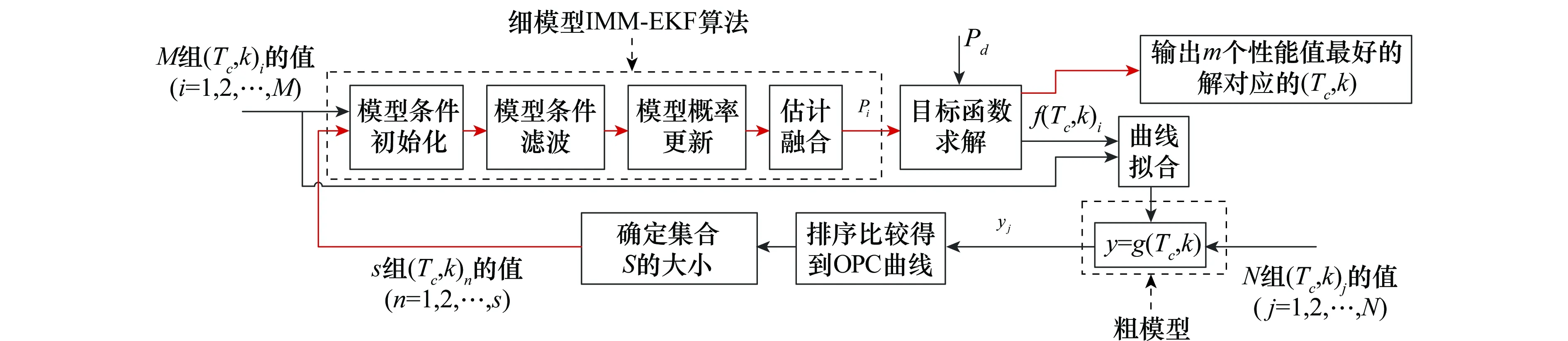
图4 RRC参数优选的OO步骤Fig.4 OO steps of RRC parameter optimization

OO的具体流程为:

(1)按机会均等原则从解空间中随机抽取M组(Tc,k)i(i=1,2,…,M)的值,其中Tc∈[Tc min,Tc max],k∈[kmin,kmax]。将这M组数据输入到细模型(即IMM-EKF算法)中进行计算,得到M组估计误差协方差矩阵Pi。

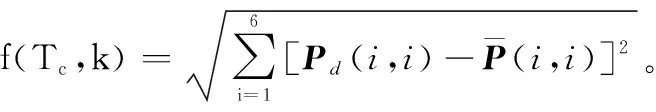
(3)将M组目标函数值和输入进行曲线拟合得到优化问题的粗模型y=g(Tc,k)。

(4)重新按机会均等原则从解空间中随机抽取N组(Tc,k)j(j=1,2,…,N)的值构成表征集合,将这N组数据输入拟合得到的粗模型中进行仿真计算,对输出yj进行排序比较,并绘出其OPC,得到OPC曲线的类型。

(5)将OPC类型所对应的z,ρ,γ,η结合式Z(m,g)=ezmρgγ+η确定选定集合S的大小s。

(6)从粗模型的输出中由小到大选取s组输出对应的输入(Tc,k)n(n=1,2,…,s),将这s组数据代入细模型中进行计算,对输出的目标函数值f(Tc,k)n(n=1,2,…,s)进行排序,从小到大选取m个值,输出这m个值对应的(Tc,k)值即为所求的足够好的解。

其中曲线拟合所用的方法为最小二乘拟合法,对于前面所述的RRC参数优化模型的最小二乘拟合,有

(14)

式中,(a1,a2,…,a6)为待定系数。

4 仿真分析

4.1 仿真环境

用于仿真的计算机性能指标如表1所示。

表1 仿真计算机性能

4.2 仿真初始条件设置

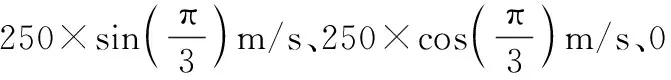
过程噪声协方差矩阵为Qk=diag[100,10,50,5,100,10],量测噪声协方差矩阵为Rk=diag[100,10,50,5,100,10]。期望协方差矩阵Pd=diag[200,30,150,20,100,10]。

对于3种模型:CV模型、匀速左转弯模型和匀速右转弯模型,模型概率为u=[0.4,0.3,0.3]T,模型转移概率矩阵为

(15)

总的仿真时间为200 s,且目标在20～60 s做匀速左转弯运动;在110～150 s做匀速右转弯运动;在其余时间则做匀速直线运动。仿真的采样时间T=1 s,目标在作匀速左转弯和匀速右转弯角速度分别为ω1=3 rad/s和ω2=-3 rad/s。假设整个过程中工作的传感器有3种:ESM系统、IRST系统和机载雷达。ESM一直处于工作状态,IRST的工作周期为3 s,雷达的工作周期为Tc。

4.3 OO求解

从解空间Tc∈[0.5,10],k∈[0.05,1]中Tc按0.5的步长、k按0.05的步长取值时,M=400,由混合控制方式得到的仿真结果如下:

将输入Tc、k及IMM-EKF的输出f(Tc,k)作为坐标系的3个轴,画出的三维图形如图5所示。拟合得到的待定系数如表2所示。

从解空间Tc∈[0.1,10],k∈[0.01,1]中选出N=10 000组输入代入粗模型(即g(Tc,k))中进行计算,其中Tc按步长0.1、k按步长0.01来选取。最终得到的10 000组解按从小到大排序后,在直角坐标系中画出的OPC曲线如图6所示。

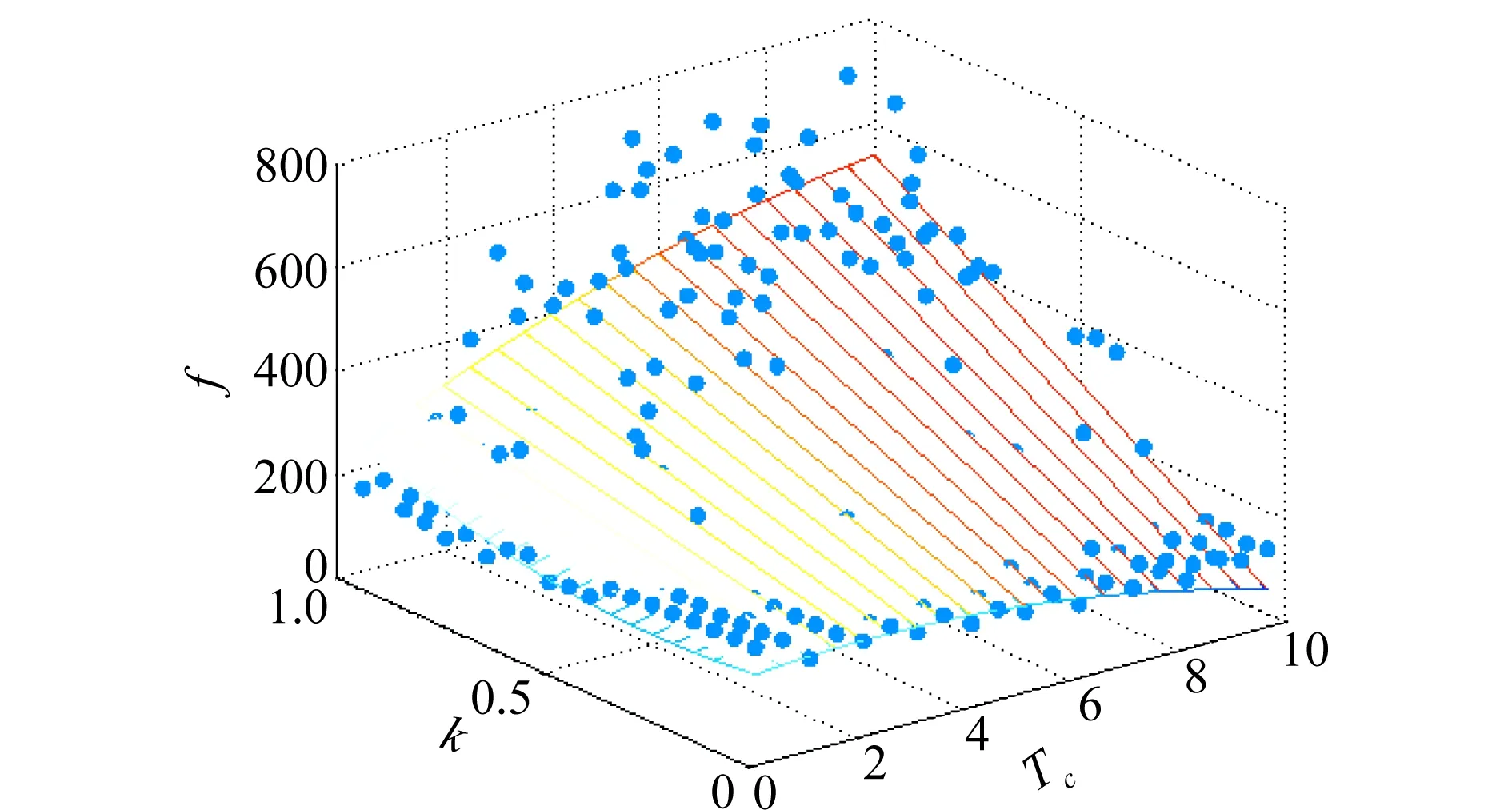
图5 Matlab拟合得到的三维图形Fig.5 3D graphics fit by Matlab

a1a2a3a4a5a6-2.074 2228.863 043.575 88.707 6-16.575 3148.912 2

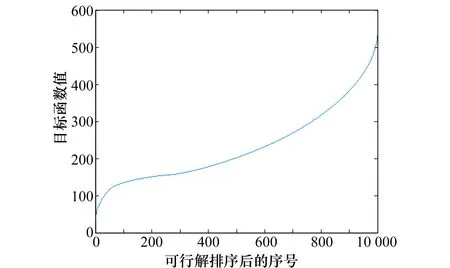
图6 OPC曲线Fig.6 OPC curve

当m=5,g=50时,噪声特性U=1时,由Z(m,g)=ezmρgγ+η得到的选定集合ΘS的大小s=83。最终得到足够好的5个解、对应的目标函数值f(Tc,k)和程序运行时间如表3所示,序号为1的解为5个解中的最优解。

表3 混合控制方式得到的足够好的解

同理,由OO的方法在等间隔辐射控制方式和实时控制方式下得到最优解,3种控制方式下的最优解情况如表4所示。

表4 3种控制方式得到的最优解

将等间隔控制、实时控制和混合控制方式得到的最优解分别代入IMM-EKF算法中,得到3种控制方式下的跟踪误差和雷达开机次数。3种控制方式的位置跟踪误差如图7所示。

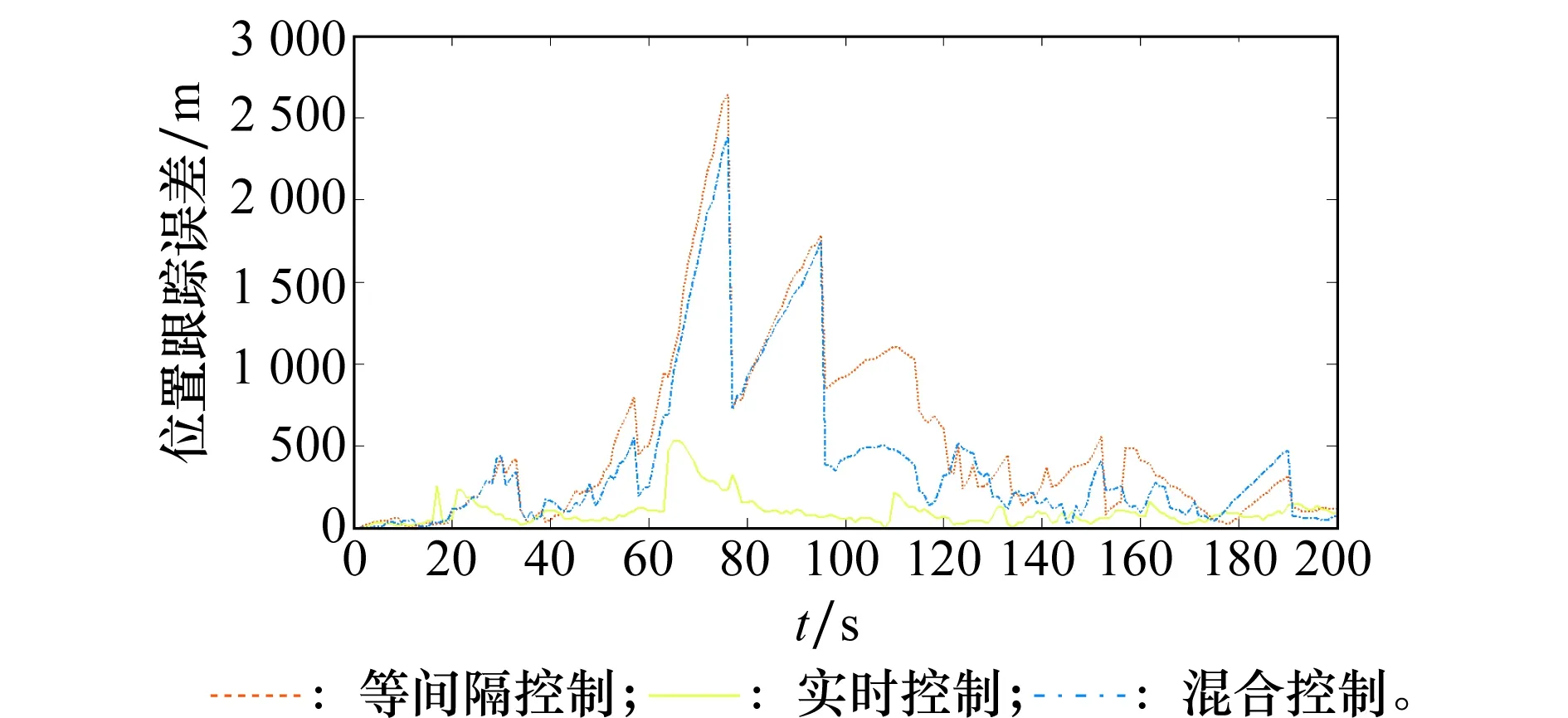
图7 3种控制方式的位置跟踪误差Fig.7 Tracking error of three control methods

由图7可以看到,实时控制方式的跟踪误差最小,跟踪性能最好;等间隔控制方式下的跟踪误差最大;混合控制方式下的跟踪误差则介于实时控制和等间隔控制之间。

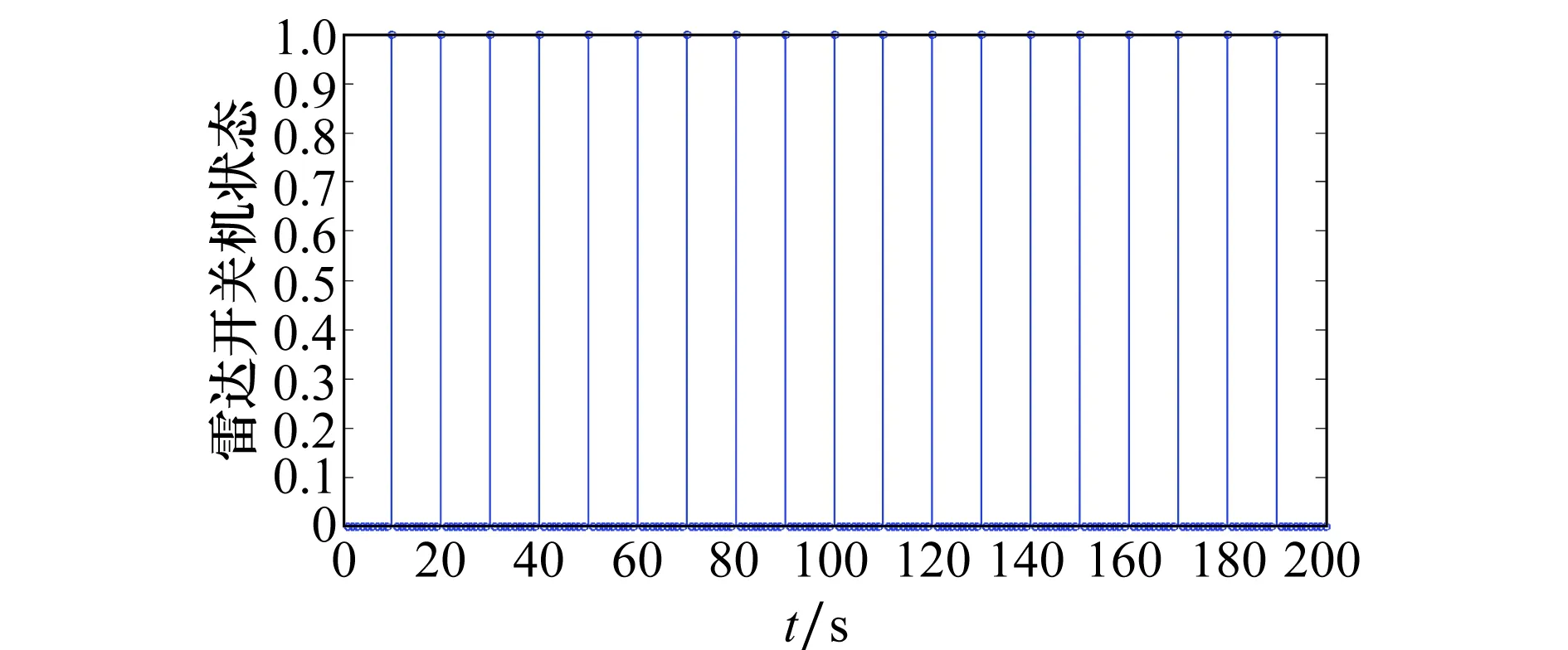
图8 等间隔控制下雷达开机次数Fig.8 Radar boot times of equal interval control

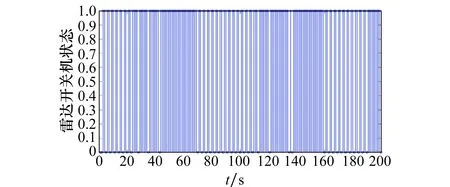
图9 实时控制下雷达开机次数Fig.9 Radar boot times of real-time control

图10 混合控制下雷达开机次数Fig.10 Radar boot times of hybrid control

而由图8～图10可以看到,实时控制的雷达开机次数最多,很容易被敌方侦察与截获,而等间隔控制的开机次数次于实时控制,混合控制的雷达开机次数最少。综上,混合控制方式可以在保证雷达开机次数较少的情况下又能达到比较好的跟踪性能。

5 结 论

本文提出MSC下的RMRC方法,基于IMM-EKF跟踪滤波算法对MSC下的RRC问题进行建模分析,基于OO方法在Matlab环境下对该模型进行仿真求解,并对仿真结果进行分析。对等间隔控制、实时控制和混合控制方式下的参数进行优化,比较了3种控制方式的跟踪结果。仿真结果证明了混合控制方式的相对优势。该方法应用于未来空战的复杂战场环境,能够在保证作战效能的前提下有效降低我方战机的被探测概率,具有较强的实战应用价值。

参考文献：

[1] BIER S G, ROTHMAN P L, MANSKE R A. Intelligent sensor management for beyond visual range air-to-air combat[C]∥Proc.of the IEEE Aerospace and Electronics Conference, 1988: 264-269.

[2] 胡笑旋, 张强. 多传感器协同管理机制研究[C]∥中国仪器仪表学会青年学术会议, 2007. HU X X, ZHANG Q. Research on multi-sensor synergistic management mechanisms[C]∥Proc.of the China Instrument Society Young Academic Conference, 2007.

[3] 徐雅薇,谢晓竹.多传感器图像融合方法及应用综述[J].四川兵工学报,2015,7(10):116-119.

XU Y W, XIE X Z. Overview of approaches and applications of multi-sensor image fusion[J].Journal of Sichuan Ordnance,2015,7(10): 116-119.

[4] 刘宁波,孙艳丽,周伟.无人机多传感器协同探测演示系统设计[J].兵器装备工程学报,2016,37(12):80-83.

LIU N B, SUN Y L, ZHOU W. Design for multi-sensor collaborative reconnaissance of unmanned aerial vehicle demonstration system[J].Journal of Ordnance Equipment Engineering, 2016, 37(12):80-83.

[5] 赵建恒, 许蕴山, 邓有为,等. 一种面向协同探测的多传感器管理系统架构[J].电光与控制, 2015(6): 6-10.

ZHAO J H, XU Y S, DENG Y W, et al. An architecture of multi-sensor management system for cooperative detection[J]. Electronic Optics and Control, 2015(6): 6-10.

[6] 武龙,许蕴山,龙文彪.一种多传感器协同探测的雷达跟踪系统[J].空军工程大学学报(自然科学版),2017, 18(1):39-43.

WU L, XU Y S, LONG W B. A radar tracking system based on cooperative detection of multi-sensor resource[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(1):39-43.

[7] SHAHBAZIAN E, BARIL L, MICHAUD G, et al. Analysis of adaptive data fusion approaches within lm canada’s technology demonstrator[C]∥Proc.of the RTO IST Symposium on Military Data and Information Fusion, 2003: 11.

[8] 贵彦乔,吴彦鸿,俞道滨. 跟踪雷达干扰技术综述[J].兵器装备工程学报,2017,38(4):141-147.

GUI Y Q,WU Y H,YU D B. Review of jamming techniques to tracker radar[J].Journal of Ordnance Equipment Engineering,2017,38(4):141-147.

[9] NASH J M. Optimal allocation of tracking resources[C]∥Proc.of the IEEE Conference on Decision and Control, 1977:1177-1180.

[10] MANYIKA J, DURRANT-WHYTE H. Data fusion and sensor management: a decentralized information-theoretic approach[M]. Prentice Hall PTR, 1995.

[11] SCHMAEDEKE W W. Information-based sensor management[C]∥Proc.of the Optical Engineering and Photonics in Aerospace Sensing, 1993: 156-164.

[12] XIONG N, SVENSSON P. Multi-sensor management for information fusion: issues and approaches[J]. Information Fusion, 2002, 3(2): 163-186.

[13] HINTZ KENNETH J, MCINTYRE G. Goal lattices for sensor management[C]∥Proc.of the Signal Processing, Sensor Fusion and Target Recognition, 1999: 249-255.

[14] KREUCHER C, KASTELLA K, III A O H. Sensor management using an active sensing approach[J]. Signal Processing, 2005, 85(3):607-624.

[15] HILAL A R, BASIR O. A collaborative energy-aware sensor management system using team theory[M]. ACM, 2016.

[16] TANG S, BI D, XU Y, et al. Dynamic sensor management algorithm based on improved efficacy function[C]∥Proc.of the IEEE International Conference on Electronic Measurement & Instruments, 2016: 1438-1442.

[17] 刘学全, 李波, 万开方, 等. 基于多传感器协同的雷达猝发技术研究[J]. 中国民航大学学报, 2012, 30(6): 17-20.

LIU X Q, LI B, WAN K F, et al. Study on radar burst technology based on multi-sensor synergy[J]. Journal of Civil Aviation University of China, 2012, 30(6): 17-20.

[18] 吴巍,柳毅,王国宏,等.辐射限制下有源无源协同跟踪技术[J].信息与控制,2011, 40(3): 418-423.

WU W, LIU Y, WANG G H, et al. Active and passive synergy tracking technique with emission constraint[J]. Information and Control, 2011, 40(3): 418-423.

[19] 吴巍, 柳毅, 杨玉山, 等. 机载多传感器协同跟踪与辐射控制研究[J]. 弹箭与制导学报, 2011, 31(1): 153-156.

WU W, LIU Y, YANG Y S, et al. The study on air-borne multi-sensor synergy tracking and radiation control[J]. Journal of Projectiles, Rockets Missiles and Guidance, 2011, 31(1): 153-156.

[20] 吴巍,王国宏,柳毅,等.机载雷达、红外、电子支援措施协同跟踪与管理[J].系统工程与电子技术,2011,33(7)：1517-1522.

WU W, WANG G H, LIU Y, et al. Airborne radar/IRST/ESM synergistic tracking and management[J]. Systems Engineering and Electronics, 2011, 33(7): 1517-1522.

[21] 钟晓军, 王国宏. 异类多传感器系统中基于跟踪质量的辐射控制研究[J]. 现代雷达, 2004, 26(2): 18-22.

ZHONG X J, WANG G H. A study on radiation control based on the tracking quality in heterogeneous sensors system[J]. Modern Radar, 2004, 26(2): 18-22.

[22] 章钊, 周峰, 张亮亮. 一种主/被动雷达协同探测跟踪算法[J]. 空军工程大学学报(自然科学版), 2013, 02:51-55.

ZHANG Z, ZHOU F, ZHANG L L. Research on active and passive radar synergistic detection and tracking algorithm[J]. Journal of Air Force Engineering University (Natural Science Edition), 2013, 02:51-55.

[23] 黄俊, 滕鹏, 于雷,等. C4ISR多传感器跟踪资源协同分配方法研究[J]. 系统仿真学报, 2009, 21(3):851-855.

HUANG J, TENG P, YU L, et al. Research on coordinated allocation of c4isr multi-sensor tracking resource[J]. Journal of System Simulation, 2009, 21(3):851-855.

[24] 马霞, 吴必富. 辐射控制下多机多传感器协同目标跟踪的分配决策数学模型[C]∥中国指挥控制大会, 2015.

MA X, WU B F. Mathematics model for multi-aircraft multi-sensor coordinated tracking target assignment policy with emission control[C]∥Proc.of the China Command and Control Conference, 2015.

[25] 戴春亮,时晨光,周建江,等.基于无源传感器协同的机载雷达自适应辐射控制算法[J].数据采集与处理,2016,31(4):746-753.

DAI C L, SHI C G, ZHOU J J, et al. Adaptive radiation control algorithm with passive sensor cooperation in airborne radar system[J]. Journal of Data Acquisition and Processing, 2016, 31(4): 746-753.

[26] 吴卫华, 江晶, 高岚. 机载雷达辅助无源传感器对杂波环境下机动目标跟踪[J]. 控制与决策, 2015, 30(2): 277-282.

WU W H, JIANG J, GAO L. Tracking maneuvering target in clutter with passive sensor aided by airborne radar[J]. Control and Decision, 2015, 30(2): 277-282.

[27] LAU T W E, HO Y C. Universal alignment probabilities and subset selection for ordinal optimization[J]. Journal of Optimization Theory and Applications, 1997, 93(3): 455-489.

[28] DENG M, HO Y C, HU J Q. Effect of correlated estimation errors in ordinal optimization[C]∥Proc.of the ACM 24th Conference on Winter Simulation, 1992: 466-474.

[29] DENG M, HO Y C. Iterative Ordinal optimization and its applications[C]∥Proc.of the 36th IEEE Conference on Decision and Control, 1997, 4: 3562-3567.

[30] LI D, LEE L H, YU C H. Constraint ordinal optimization[J]. Information Sciences, 2002, 148(1):201-220.

[31] 李波,刘学全,高晓光.基于BP网络和序优化方法的火控攻击方案寻优[J].系统工程与电子技术,2013,35(9):1886-1990.

LI B, LIU X Q, GAO X G. Fire control attack scheme optimization based on BP network and ordinal optimization[J]. Systems Engineering and Electronics, 2013, 35(9): 1886-1990.