基于深度卷积神经网络的PolSAR图像变化检测方法
王 剑, 王英华, 刘宏伟, 何敬鲁
(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071; 2. 西安电子科技大学信息感知技术协同创新中心, 陕西 西安 710071)
0 引 言
遥感图像变化检测技术用于检测同一地点在某一段时间内发生的变化,在灾害监测、土地调查和目标侦查等民用和军用方面具有广泛的应用[1-2]。近年来,有关极化合成孔径雷达(polarimetric synthetic aperture radar,PolSAR)图像变化检测的研究受到越来越多的关注。PolSAR系统受天气条件和光照条件的影响较小,其数据不仅能够提供幅度信息,还可以描述目标的散射特性,进一步提供有关场景地物更加丰富的信息,因此在图像解译中比单极化合成孔径雷达(synthetic aperture radar,SAR)更具优势[3]。
遥感图像变化检测步骤一般包括:图像预处理,差异图提取及变化二值图生成[1]。由于PolSAR数据的特点,传统的PolSAR变化检测的研究主要集中于统计方法。2003年,文献[4]提出了基于Wishart似然比检验统计量的变化检测方法,通过2幅PolSAR图像中相同位置像素的协方差矩阵相似性检验,实现PolSAR图像变化检测;2014年,文献[5]利用异质杂波模型实现PolSAR图像变化检测;2016年文献[2]基于矩阵相似性的思想,提出了基于Hotelling-Lawley Trace检验统计量的变化检测方法;此外,文献[6-7]提出了基于超像素和Wishart分布的变化检测方法以及基于超像素和混合Wishart分布的变化检测方法;文献[8]提出了结合超像素和多数投票的变化检测方法;近年来,在单极化SAR及高光谱图像变化检测方面,文献[9-11]提出了多种基于机器学习与深度学习的变化检测算法,取得了重要的进展,同时也提供了新的研究思路。
文献[2,4-5]均为基于统计建模的方法,而文献[6-8]都使用了超像素分割并对Wishart似然比方法做了改进,但上述方法存在3个问题:
(1)对PolSAR数据统计建模不能够完全精确地拟合原始PolSAR数据的分布,导致所得结果不够准确,产生大量的虚警。
(2)基于检验统计量的方法都需要设定虚警率或显著性水平以获得阈值用于判别,不同参数产生的结果差异较大,且无法实现自动检测。
(3)使用简单的超像素分割可能会造成误分割,造成检测结果不够准确。
针对以上问题,受到文献[9-12]的启发,本文提出了结合深度学习的PolSAR变化检测方法,具体流程如图1所示。

图1 基于DCNN的PolSAR图像变化检测方法Fig.1 PolSAR image change detection method based on DCNN
本文方法具有以下特点:
(1)结合二时相PolSAR图像的共有信息和各自特有信息,实现联合超像素分割与合并,更准确地提取空间信息。
(2)利用深度卷积神经网络(deep convolutional neural network,DCNN)在分类任务当中的优势,将变化检测问题转化为分类问题进行处理,训练DCNN并用于分类。
1 基于区域信息的差异图生成
1.1 二时相PolSAR图像联合超像素分割与合并
超像素分割在遥感图像处理当中具有广泛的应用[13-15]。为了实现二时相图像的超像素分割,同时结合2幅图像的共有和特有信息得到一致的超像素分割结果,本文使用文献[8]中的PolSAR联合超像素分割方法将图像分割为Ns个超像素区域,得到分割结果S。
为进一步提取空间信息,本文在文献[14]提出的单幅单极化SAR图像超像素合并方法的基础上进行修改,实现了二时相多极化SAR图像的联合超像素合并。在合并过程中,对于2幅PolSAR场景共有的同质区域,进行超像素合并;而对于场景复杂区域,不进行超像素合并。场景复杂区域指的是呈现为纹理复杂、散射机制变化剧烈以及强度变化剧烈的区域,为了保持这类区域中边界的完整和准确,有必要在区域内不进行超像素合并操作。以下4个准则用于实现联合超像素合并。
邻接准则[14]。该准则就是要找到相邻的超像素对,服从式(1)
(1)
式中,si和sj代表联合分割之后的任意2个超像素。C1(i,j)是表示任意2个超像素是否具有邻接关系的量。C1(i,j)=1时,超像素si与sj是邻接的;C1(i,j)=0时,则超像素si与sj不具有邻接关系。
相似性准则。直接将文献[14]中的相似性准则特征提取方法运用于二时相PolSAR对数功率图,得到任意超像素si的特征向量K1(i)和K2(i)(i代表超像素标号,式(2)中j表示与i不同的超像素标号,下标表示PolSAR图像序号)。相似性准则定义为
C2(i,j)=‖[K1(i),K2(i)]-[K1(j),K2(j)]‖1
(2)
式中,[A,B]符号表示将2个特征向量A与B连接构成一个新的特征向量的操作;‖ · ‖1表示1范数距离。式(2)中,[K1(i),K2(i)]表示超像素si在第1和第2时相图像当中的特征向量连接而成的新的特征向量,[K1(j),K2(j)]同理。因此,C2(i,j)表示了超像素对(si,sj)在特征空间中的距离。
空间连续性准则[14]。该准则的目的是在合并超像素的同时保持边缘结构不被破坏。类似于文献[13]中纹理特征向量的提取,运用4种尺度的Prewitt核[16]对PolSAR对数功率图提取边缘特征,可以得到超像素的边缘特征向量H1(i,j)和H2(i,j)。由此定义空间连续性准则为
C3(i,j)=
(3)
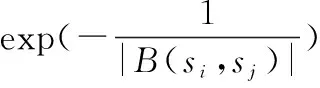
Wishart距离准则。该准则用到PolSAR图像的Wishart距离w1(i,j)与w2(i,j)(第一和第二时相中超像素si与sj的Wishart距离[4])。该准则计算公式为
C4(i,j)=‖[w1(i,j)w2(i,j)]‖1
(4)
式中,w1(i,j)表示超像素对(si,sj)在第一时相的Wishart距离,而w2(i,j)表示他们在第二时相的Wishart距离。实际上,C4(i,j)通过Wishart距离度量了超像素对(si,sj)在散射机制和强度上的差异度,C4(i,j)的值越大,表示超像素对之间的差异越大,反之越小。
根据上述4个准则,计算得到任意超像素对(si,sj)之间的4个归一化准则量C1(i,j)、C2(i,j)、C3(i,j)和C4(i,j)。为了实现超像素合并,首先根据邻接准则C1(i,j)找到邻接的超像素对,D1表示超像素分割后所有邻接超像素对的集合,即
D1={(si,sj)|C1(i,j)=1,i≠j,i,j=1,2,…,Ns}
(5)
再根据其余3条准则确定要合并的超像素,即
D2={(si,sj)|Ck(i,j)≤β,(si,sj)∈D1,k=2,3,4}
(6)
D2为需要合并的超像素对的集合,其中β为[0,1]区间内的值,需要预先设定。为了验证β对超像素合并的影响,设置不同的β值进行超像素合并。通过对比实验发现,当β值设置过小时,超像素合并不完全,出现欠合并的现象;当β值设置过大时,出现过度合并的现象;而β取值在[0.16,0.2]时,能够达到较好的合并效果,因此本文当中将β设定为0.16。
图2给出了局部区域的联合超像素分割及合并的结果图。为了更好地反映分割与合并算法的效果,使用PolSAR图像的Pauli伪彩色图[3]表示原图像,如图2(a)和图2(b)所示。图2(c)与图2(d)分别是图2(a)与图2(b)经过联合超像素分割的结果,超像素边界用白色线表示,2幅图像的分割区域完全一致,同时分割考虑了2幅图的特有信息,即对于图2(a)或图2(b)当中特有的区域,如发生变化的区域,也能够很好地实现分割。图2(e)和图2(f)是在图2(c)与图2(d)的基础上,进行超像素合并后的结果。
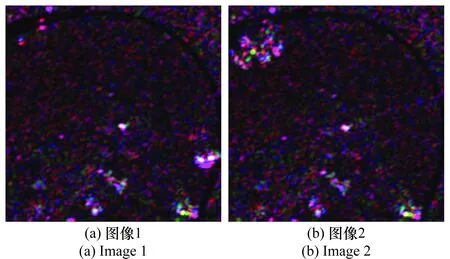

图2 局部区域联合超像素分割结果与合并结果Fig.2 Joint super pixel segmentation results and merging results in local area
从图2中可以观察到,在同质区域,实现了超像素合并,将同质区域当中的超像素合并在一起,形成了一个或有限几个面积较大的超像素块;而在场景复杂区域中,没有进行超像素合并,该区域内超像素仍保持较小的面积。
1.2 结合空间信息的Wishart似然比差异图
超像素合并之后,使用基于区域的Wishart距离可以得到差异图。区域级Wishart距离[15,17]定义如下
(7)

(8)
式(8)表示基于超像素的PolSAR变化检测差异度量计算方式,与式(7)的区别在于,d(si)表示了二时相图像在同一超像素区域si的差异。当前存在的问题是,联合合并之后超像素大小是不均匀的,即存在N同质区域超像素≫N非同质区域超像素的情况,由图2也可观察到该结论。此现象导致同质区域间的差异值远远大于非同质区域间的,这与实际情况相违。基于以上原因,本文修改距离公式得到以下差异度量为
(9)
式(9)是用参数Ni归一化后的距离度量公式,保持距离的合理性的同时去掉了Ni对距离计算的影响,使距离计算正确且与实际情况相符。通过使用合并后的超像素标记计算差异值,一定程度上去除了同质区域相干斑噪声的影响,同时由于场景复杂区域内的超像素未合并,该区域的边缘特征得到保持,提升了差异图中变化区域形状信息表示的准确性。
2 预分类算法
预分类算法是为了获得大量有标号的样本用于训练神经网络及初次划分图像场景。本文的预分类算法改进了文献[18]所提的预分类算法。原方法中阈值设定过程涉及到差异图特征提取、聚类及参数设置等步骤。本文方法在此基础上进行改进。首先对差异图进行大尺度的中值滤波,一定程度消除相干斑带来的影响。窗口尺寸一般设为30×30,然后用模糊C均值聚类(fuzzy C mean clustering,FCM)算法[19]依据像素幅值进行二类分类,根据分类结果获得变化类的样本数T,将其设定为阈值。利用中值滤波的平滑效果,差异图中反映变化的区域将扩大,同时部分由相干斑噪声引起的面积很小的伪变化区域被去除。改进后的方法相比于原始方法[18]可以获得更多的正负类伪训练样本,更好的鲁棒性能,且能够实现阈值的自动化选择。除阈值设定外,其余步骤与原始方法一致。
使用上述方法可以获得预分类结果图像I,I中像素被分为3类:变化类、待确定类和未变化类,在图像中分别由标号1、0.5和0表示。为了提高样本的置信度,按如下方式进一步处理结果I:对结果图像I中的像素点(x,y),用Lx,y表示该像素点的标号,若Lx,y=0.5,则保持该点标号不变;否则,取其5×5的邻域作为操作区域,若操作区域当中有超过一半的像素标号与Lx,y一致,则保持(x,y)的标号不变,否则将Lx.y置为0.5,即将该样本点划分到待确定类。最终预分类算法将整个图像场景分为3类,即变化类(L=1),未变化类(L=0)及待确定类(L=0.5)。
3 基于DCNN的PolSAR图像变化检测
深度学习在单极化SAR图像处理当中已经得到了广泛的应用,但在多极化SAR图像处理领域应用较少。文献[12]在2016年提出了基于DCNN的PolSAR图像分类算法,相比于传统方法取得了更好的结果,表明了深度学习在PolSAR图像处理中提取特征和分类方面的优势,受到该方法及一系列基于深度学习的单极化SAR图像变化检测方法[9-11]的启发,本文提出了基于DCNN的PolSAR图像变化检测算法。
3.1 PolSAR图像特征选择与数据标准化
3.1.1 PolSAR图像特征选择
全极化SAR数据由4个通道构成,分别为SHH、SHV、SVH和SVV(下标第1个字母代表接收极化方向,第2个字母代表发射极化方向)。单站情况下,SHV=SVH,一般使用大小为3×3的极化协方差矩阵或者极化相干矩阵描述每一像素点处的散射信息[3]。
为了更有效地训练DCNN,从原始图像数据中每一像素点处提取6种原始特征构成网络输入,即
(10)
式中,SPAN表示散射功率;T22代表极化相干矩阵对角线上的第2个元素;T33代表极化相干矩阵对角线上的第3个元素,其中A、B、C特征来自极化相干矩阵,分别反映了散射总功率、方向为0°的偶次散射及方向为45°的二面角散射[3];D、E、F分别表示Pauli极化分解[3]伪彩色图像的3个通道。本文A、B、C特征取自文献[12]。对于文献[12]中的其他特征,通过分析其在变化检测当中的可分性,发现可分性不够好,因此去掉了这些特征。根据文献[20],PolSAR数据经过Pauli分解和伪彩色编码得到的伪彩色特征对于分类有提升效果,也能更好地突出变化区域的形状和轮廓信息,所以在特征A、B、C的基础上,加入Pauli伪彩色图的3通道作为补充,进一步提升特征的整体可分性。
3.1.2 数据标准化
为实现像素级上的分类,需要构建以像素为中心的特征表达作为网络的原始输入。本文方法中,提取以任意坐标(x,y)为中心的s×s(s代表像素点数,且s为奇数)邻域中所有像素点的6种特征作为(x,y)的特征表达,即得到尺寸为s×s×6的特征表示。具体到变化检测任务,两幅图像在(x,y)坐标处对应的特征分别记为p1(x,y)和p2(x,y),将p1(x,y)和p2(x,y)按数据维度的第一维联结起来,即拼接成大小为2s×s×6的联合特征。对训练集、验证集、测试集样本都需要进行数据标准化操作,操作后所得的联合特征数据将用于后续的训练和测试过程。
3.2 DCNN结构
本文使用的DCNN连接类似于经典的AlexNet[21]与文献[12]的网络结构,结构如图3所示。假定输入数据大小为m×n×c,在卷积层Conv1,需要进行P=2的空间填充,此时数据尺寸为(m+4)×(n+4)×c,用20个3×3×c的卷积核实现卷积操作,生成维度(m+2)×(n+2)×20的数据。池化层功能相当于下采样,可以削减数据大小和权值数,本方法中池化层都采用最大值池化[21]。在池化层P1,由于本文输入数据设定为2s×s,其中s为奇数,卷积后数据的第2维无法进行步幅为2的池化,因此需要在池化之前在第2维做P=1的零填充,然后进行2×2的最大值池化,输出维度(m/2+1)×((n+1)/2+1)×20的数据。在卷积层Conv2,首先进行P=1的零填充操作,此时数据大小为(m/2+3)×((n+1)/2+3)×20,经50个3×3×20的卷积核操作得到维度(m/2+1)×((n+1)/2+1)×50的输出。在池化层P2,池化后的数据尺寸为((m+2)/4)×((n+3)/4)×50。全连接层F1输出大小为1×1×500。F1后接ReLU激活函数[21]实现非线性变换并加速算法收敛。全连接层F2有2个输出,其后接Softmax Loss层[22],输出的2个值分别表示样本属于变化类与非变化类的概率,最终据此概率判断输入样本的类别。

图3 DCNN结构Fig.3 Architecture of DCNN
3.3 训练DCNN
本文采用经典方式训练DCNN,损失函数为交叉熵函数[22],使用冲量随机梯度下降算法[23]在反向传播过程中更新参数,使用文献[12]中深度卷积网络的更新规则进行更新,具体表示为

(11)
ωi+1=ωi+vi+1
(12)
式中,ωi代表第i次迭代的权值参数;L表示损失函数。
式(11)中,冲量参数设为0.9,权值衰减系数(weight-decay)设为0.000 5,i代表迭代次数,vi代表第i次迭代时的速度参数,ε表示学习率。此外,学习率的设定方式也与文献[12]中的更新方式相同。训练开始之前,网络中所有权值和偏置用均值为0、方差为0.01的高斯分布随机初始化,速度值v初始化为0。
4 实验结果
为了验证本文算法的有效性,在实测数据上进行变化检测实验,同时与多种PolSAR变化检测方法进行对比。使用制图精度、用户精度、总体分类精度及Kappa系数[24]等指标对多种算法的实验结果进行评估。本文使用的实验数据是由美国空军实验室(airforce research laboratory,AFRL)提供的X波段三通道PolSAR数据[25],实验所用数据为2幅三通道PolSAR图像,场景大小均为1 501×1 501,两幅图像发生的变化主要为车辆的移动,具体可见图4。图4(a)与图4(b)分别是实验当中所使用的原始PolSAR数据的Pauli分解伪彩色图像,图4(a)是第一时相的伪彩色图,图4(b)是第二时相的伪彩色图,图4(a)与4(b)的不同之处就是场景中的车辆发生了移动,产生了变化。图4(c)是人工标记的Groundtruth图像,反映了真实的车辆变化区域。

图4 实验图像和参考图像Fig.4 Experiment images and Groundtruth image
利用本文所提算法及像素级Wishart似然比检测[4](记为Wishart)、基于HLT检验统计量的变化检测[2](Hotelling-Lawley Trace Statistic,记为HLT)、似然比变化检测算法[26](记为LR)、超像素级Wishart似然比检测[6](记为Region Wishart)、基于超像素和多数投票(method based on superpixel and majority voting,SMV)[8]等方法对所选数据进行实验。Wishart(0.005)表示在显著性水平为0.005时的检测结果,Wishart(k-means)表示对检验统计量进行k-means聚类的实验结果,HLT(0.005)和HLT(k-means)意义也同上。LR(0.1)表示阈值设为0.1的结果。实验参数设置方面,为了验证邻域大小对实验结果的影响,分别使用3×3、5×5、7×7、9×9的邻域数据构建训练集数据、验证集数据和测试集数据,数据当中每一个样本的大小分别为6×3×6、10×5×6、14×7×6和18×9×6,相应地将这4种样本训练的DCNN简称为DCNN1、DCNN2、DCNN3和DCNN4,通过实验结果对比将DCNN4结果作为本文结果。此外,在实验当中,超像素分割尺度设为3,合并准则阈值β设为0.16,其余参数如上文所述。实验结果在表1和图5当中给出。由于预分类算法获得的伪训练样本中存在严重的类别不平衡现象,因此对少数类即变化类采用翻转和复制的方式进行数据扩充,一定程度上改善了类别的不平衡程度。
表1中,Pc(producer’s accuracies of changed)与Pu(producer’s accuracies of unchanged)分别表示变化类和未变化类制图精度[5,7],Uc(user’s accuracies of changed)与Uu(user’s accuracies of unchanged)分别表示变化和未变化类用户精度[5,7],FA(number of false alarms)、MA(number of missed alarms)、Pcc与Kappa分别表示虚警数、漏警数、总体分类精度及Kappa系数[24]。
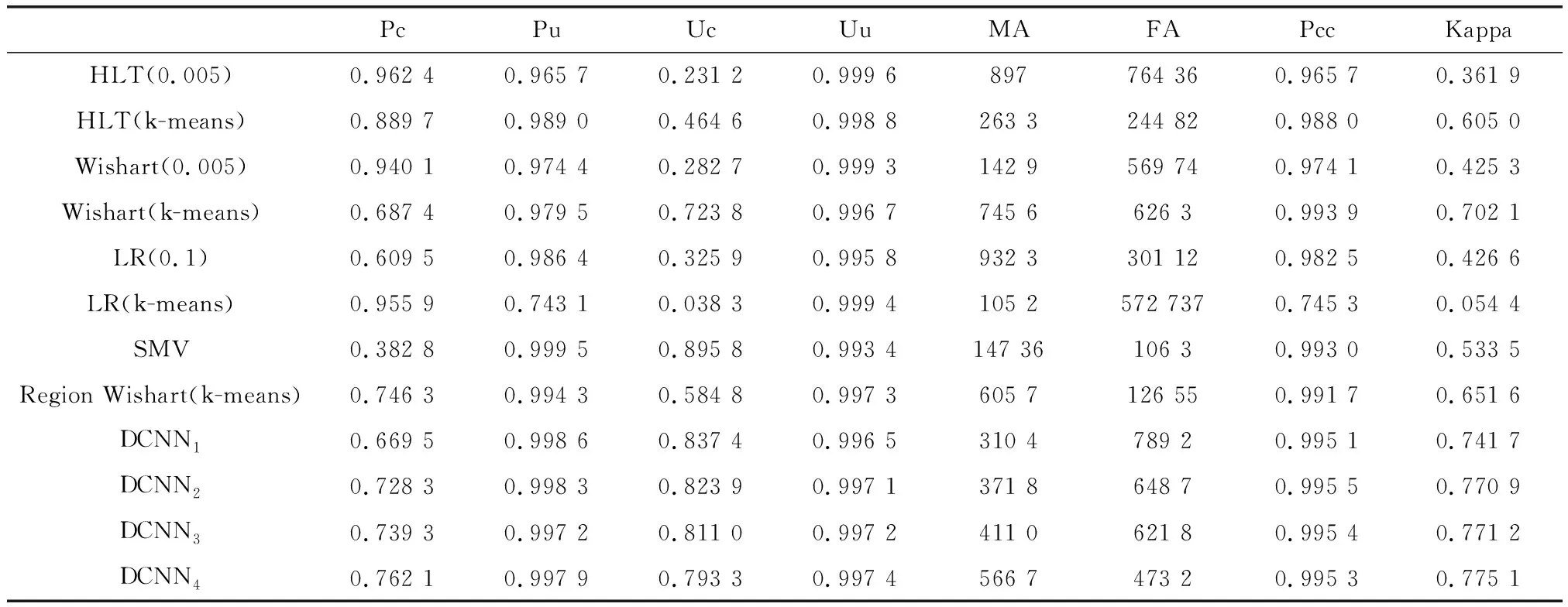
表1 多种变化检测方法性能参数比较

图5 实验结果对比Fig.5 Comparison of experimental results
由表1中的性能参数对比及图5中实测数据实验结果对比可知,本文方法DCNN4的结果相比于其他方法更具优势。相对于本方法而言,统计建模方法能够获得较高的检测率,同时虚警率也很高,这是由于不能够对数据进行精确的统计建模造成的;对于运用超像素分割的方法,分割的不准确性或所选择的特征对于不同数据的表现不同都会导致超像素方法的不稳定。本文方法首先借助联合超像素合并的空间信息得到了类别的粗划分结果,然后训练神经网络可以从数据本身学到优化的特征表达用于分类任务,避免了统计建模或超像素分割的不准确性带来的误差。由图5看出,本文所提方法的检测结果与人工标注的参考图更加接近,检测区域更平滑与集中,能够更加准确地反映变化区域的形状。
通过对比多种方法所得到的实验结果与性能参数,可以总结出本文方法相对于传统方法具有以下优点:①本文方法能够很大程度降低相干斑噪声的影响。从结果图中可以看出,相对于大部分传统算法,本文结果的虚警点数更少;②本文方法结合超像素合并与DCNN训练,能够较好地保持变化区域的轮廓信息,由图5及表1中Pcc和Kappa系数等参数的对比可以证明本文方法对变化区域轮廓刻画的准确性比传统方法更高。
5 结 论
本文以PolSAR图像变化检测为目的,构建了以DCNN为中心的变化检测算法,将变化检测问题转换为分类问题加以解决,实现了自动的、无监督的变化检测。本方法结合了空间和像素的信息,通过两种信息的交互使用,一定程度克服了单独使用像素级或者超像素级的方法的缺点。同时,利用DCNN在特征提取和分类方面的优越性,在保持较高检测率的同时将虚警控制在较低的水平,提高了算法的稳定性,相比于传统算法具有更好的性能。
参考文献:
[1] 公茂果, 苏临之, 李豪, 等. 合成孔径雷达影像变化检测研究进展[J].计算机研究与发展, 2016, 53 (1): 123-137.
GONG M G, SU L Z, LI H, et al. A survey on change detection in synthetic aperture radar imagery[J]. Journal of Computer Research and Development, 2016, 53 (1): 123-137.
[2] AKBARI V, ANFINSEN S N, DOULGERIS A P, et al. Polarimetric SAR change detection with the complex hotelling-lawley trace statistic[J]. IEEE Trans.on Geoscience and Remote Sensing, 2016, 54(7): 3953-3966.
[3] LEE J S, POTTIER E. Polarimetric imaging: from basics to applications[M]. Boca Raton, FL: CRC Press, 2009.
[4] CONRADSEN K, NIELSEN A A, SCHOU J, et al. A test statistic in the complex Wishart distribution and its application to change detection in polarimetric SAR data[J]. IEEE Trans.on Geoscience and Remote Sensing, 2003, 41(1): 4-19.
[5] LIU M, ZHANG H, WANG C. Change detection of multilook polarimetric SAR images using heterogeneous clutter models[J]. IEEE Trans.on Geoscience and Remote Sensing, 2014, 52(12): 7483-7494.
[6] YANG W, SONG H, XIA G S, et al. Dissimilarity measurements for processing and analyzing PolSAR data: a survey[C]∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium, 2015: 1562-1565.
[7] YANG W, YANG X L, YAN T H, et al. Region-based change detection for polarimetric SAR images using Wishart mixture models[J]. IEEE Trans.on Geoscience and Remote Sensing, 2016, 54 (11): 6746-6756.
[8] XIE L, ZHANG H, WANG C, et al. Superpixel-based PolSAR images change detection[C]∥Proc.of the 5th IEEE Asia-Pacific Conference on Synthetic Aperture Radar,2015: 792-796.
[9] GONG M G, ZHAN T, ZHANG P Z, et al. Superpixel-based difference representation learning for change detection in multispectral remote sensing images[J]. IEEE Trans.on Geoscience and Remote Sensing, 2017, 55(5): 2658-2673.
[10] GONG M G, ZHAO J J, MIAO Q G, et al. Change detection in synthetic aperture radar images based on deep neural networks[J]. IEEE Trans.on Neural and Learning Systems, 2016, 27(1): 125-138.
[11] LI Y, GONG M G, JIAO L C, et al. Change-detection map learning using matching pursuit[J]. IEEE Trans.on Geoscience and Remote Sensing, 2015, 53(8): 4712-4723.
[12] ZHOU Y, WANG H, XU F, et al. Polarimetric SAR image classification using deep convolutional neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1935-1939.
[13] WANG Y H, LIU H W. PolSAR ship detection based on superpixel-level scattering mechanism distribution features[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1780-1784.
[14] YU H, ZHANG X R, WANG S, et al. Context-based hierarchical unequal merging for SAR image segmentation[J]. IEEE Trans.on Geoscience and Remote Sensing, 2013, 51(2): 995-1009.
[15] HE J L, WANG Y H, LIU H W, et al. A novel automatic PoLSAR ship detection method based on superpixel-level local information measurement[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(3): 384-388.
[16] HARALICK R M. Digital step edges from zero crossing of second directional derivatives[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence, 1984, 6(1): 58-68.
[17] CAO F, HONG W, WU Y, et al. An unsupervised segmentation with an adaptive number of clusters using the SPAN/H/α/a space and the complex Wishart clustering for fully polarimetric SAR data analysis[J]. IEEE Trans.on Geoscience and Remote Sensing, 2007, 45(11): 3454-3467.
[18] GAO F, DONG J, LI B, et al. Automatic change detection in synthetic aperture radar images based on PCANet[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1792-1796.
[19] BEZDEK J C, EHRLICH R, FULL W. FCM: the fuzzy c-means clustering algorithm[J].Computers and Geosciences,1984,10(2): 191-203.
[20] UHLMANN S, KIRANYAZ S. Integrating color features in polarimetric SAR image classification[J]. IEEE Trans.on Geoscience and Remote Sensing, 2014, 52(4): 2197-2216.
[21] KRIZHEVSKY A, SUTSKEVER I, HINTON G E, et al. ImageNet classification with deep convolutional neural networks[C]∥Proc.of the Advances in Neural Information Processing Systems, 2012: 1097-1105.
[22] XU C, LU C, LIANG X,et al. Multi-loss regularized deep neural network[J]. IEEE Trans.on Circuits and Systems for Video Technology, 2016, 26(12): 2273-2283.
[23] POLJAK B T. Some methods of speeding up the convergence of iterative methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1-17.
[24] STEHMAN S V. Selecting and interpreting measures of thematic classification accuracy[J]. Remote Sensing of Environment, 1997, 62(1): 77-89.
[25] SCARBOROUGH S M, GORHAM L R, MINARDI M J, et al. A challenge problem for SAR change detection and data compression[C]∥Proc.of the International society for optical Engineering, 2010: 1-5.
[26] FERRO-FAMIL L, NEUMANN M. Recent advances in the derivation of PoL-inSAR statistics: study and applications[C]∥Proc.of the 7th European Conference on Synthetic Aperture Radar, 2008: 1-4.

