基于PO/AP的角反射体RCS模型构建及分析

张 俊, 胡生亮, 王 聘, 范学满

(海军工程大学兵器工程学院, 湖北 武汉 430033)

0 引 言

角反射体是一种重要的雷达无源对抗器材,通过对雷达入射波的强烈反射,形成假目标实现对雷达的干扰[1-3],其通常由2块或3块金属板构成的两面角或三面角结构组成,在舰艇、飞机、导弹等军用目标上经常出现,是军用目标侧视方向的强散射源[4]。早在二战的诺曼底登陆行动中,盟军通过在加莱地区投放大量角反射体,成功吸引了德军的注意力,为登陆成功奠定基础;美越战争中,越军曾使用由多个角反射体串联成的角反射体阵列模拟大桥的电磁散射特性,对清化大桥形成了有效的掩护。自此,各国部队都开始大量列装各型角反射体[5]。

雷达截面积(radar cross section, RCS)是雷达目标的一类关键电磁散射特性,是度量目标对雷达散射能力的一个重要物理量[6-8]。当三面角反射体各平板相互正交时,在一个很宽的观察角范围内能够呈现出很大的RCS,从而可以有效干扰跟踪雷达、无线电信标等目标。此外,高效、准确地分析角反射体的后向散射特性,也是预估其他各类军用目标RCS的重要基础[9-12]。

鉴于角反射体RCS特性的重要性,许多专家学者已对其展开了深入的研究。文献[13-17]分别采用复射线(complex rays, CR)、高斯光束(Gaussian beams, GB)、射线弹跳(shooting and bouncing rays, SBR)、戈登表面积分法(Gordan surface intergral, GSI)和几何光学法(geometric optics, GO)对三面角反射体RCS进行预估,这几种算法虽然能以曲线形式给出三面角反射体RCS的预估结果,但均未能给出其全向RCS的完整表达式,同时由于这几种方法计算量大,实际可操作性和拓展性不强。文献[18]首次利用几何光学/区域投影法(geometrical optics/area projection, GO/AP)给出了三面角反射体RCS表达式,但未给出具体推导过程；文献[19]在此基础上继续利用GO/AP算法建立了一套三面角反射体RCS预估通用模型,并对原始算法进行了改进,拓宽了算法对方位角和俯仰角的适应性,仿真验证了RCS模型的有效性。虽然通过AP法确定有效面积过程简便,但是由于采用的GO法仍是一种高频近似的方法,电磁波被近似为波长为零的光束,因此无法展开入射波极化方式分析。文献[20-21]开始利用物理光学(physical optics, PO)法分析三面角反射体RCS特性,但确定照射区域过程均繁琐复杂,使得单一PO法无法后续推广应用于结构更加复杂的异形角反射体,可移植性较差,此外上述研究同样未将入射波极化方式纳入RCS模型,也未对各种反射类型对整体RCS贡献展开分析。

为全面深入掌握角反射体全向RCS特性,针对上述研究现状的不足,笔者综合PO法全面、直观及AP法简洁、高效的特点,构建了基于PO/AP的三面角反射体全向RCS模型,研究了包括角反射体形状、尺寸,以及入射波方位角φ、俯仰角θ、频率f、极化方式等参数在内的角反射体RCS特性,同时为了得到每种反射对角反射体整体RCS的贡献,对结果及3种反射类型进行了独立分析,最后通过FEKO仿真对算法的有效性进行了验证。

1 角反射体全向RCS模型构建

建立坐标系并定义各类参数是构建角反射体全向RCS模型的前提,在此基础上从PO法基本原理方程中得出与本问题相适应的计算公式,并基于AP法确定各种反射类型下的照射区域,从而构建起最终的角反射体全向RCS模型。

1.1 角反射体概述

角反射体根据几何结构(平板面形状)的不同通常可分为:方形、三角形、圆形3种类型,如图1所示。构成角反射体的每个表面可认为是理想导体板,假设其垂直边长为a(本文不妨令a=0.5 m)。

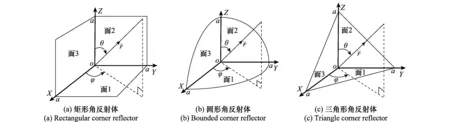
图1 三面角反射体几何结构Fig.1 Geometry of trihedral corner reflector

角反射体的最大反射方向即为角反射体的中心轴,他与3个垂直轴的夹角相等,等于54°45′。通常情形下,当反射物体的有效面积为Ae时,其RCS表示[22]为

(1)

式中,λ为入射电磁波波长。

由于式(1)可以应用于确定角反射体的RCS的具体数值,所以在设计中通常使用该方程式。然而,为了进一步角反射体RCS相对于入射角的性质,需要进一步考虑入射波的角度、频率、极化方式、反射次数等。

1.2 基于PO的角反射体全向RCS模型

1.2.1 PO算法概述

根据PO法原理方程基本理论,当电磁波入射在导体表面上会激发感应电流,从而电磁波被重新辐射,在与入射波的辐射源相同位置处的接收点处,能够观测到来自角反射体的反射波,从而得到RCS[23-25]。

(2)

1.2.2 PO算法应用

将第1.2.1节中所述PO法原理方程应用于图1所示的角反射器的模型,并导出表达角反射体全向RCS的入射角特性的表达式。

首先,设置入射磁场Hi表达式[17]为

(3)

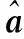
(4)

Ax=-cos(90-η)cosφcosθ-sin(90-η)sinφ

Ay=-cos(90-η)cosθsinφ+sin(90-η)cosφ

Az=cos(90-η)sinθ

式中，η是入射电场的极化角度(垂直极化为0°,正向为顺时针)。

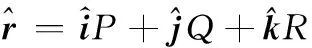
(5)

P=cosφsinθ

Q=sinφsinθ

R=cosθ

电磁波的入射范围为

0°≤θ≤90° 0°≤φ≤90°

需要指出的是,当反射场是由单个导体板中的一次反射决定的情形下,等式(3)可以直接代入等式(2),在本文所处理的三面矩形角反射体中,认为PO反射在每个表面上重复多次,然后在到达方向上再辐射,因此考虑3种类型的反射,1次反射、2次反射和3次反射。对于3次以上的多次反射,由于反射面的数量是3个,且它们是正交的,所以认为影响很小,所以在这里被忽略。根据上述分析将入射磁场分类如下:

Hi|l:入射波入射在表面l上的磁场;

Hi|l→m:入射波首先在表面l上反射然后入射到表面m上,表面m上的入射磁场;

Hi|l→m→n:入射波首先在表面l反射然后在表面m反射并入射在表面n上时,表面n上的入射磁场。

这里,l,m和n是表示反射器表面的后缀,1表示面1,2表示面2,3表示面3。由于l≠m≠n,总共考虑了15种类型的入射场,分别有单次反射3种类型,2次反射和3次反射各6种类型。

对应于每种类型的入射场分析如下:首先,在单次反射的情形下,当面l反射时的入射磁场Hi|l为

(6)

在2次反射的情况下,对于入射磁场,应考虑到达观测点前的最后反射面上的磁场,如果电磁波以面l和面m的顺序进行反射,入射到面m的磁场Hi|l→m为

(7)

类似地,3次反射的入射磁场Hi|l→m→n由式(8)给出。

(8)

在观测点处的总的反射磁场Hs被认为是上述对入射磁场的再辐射的贡献的组合。

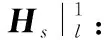
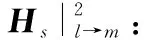
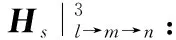
考虑不同的反射次数和反射顺序,观测点反射磁场可以相应分解为表1所示的总共15种类型。

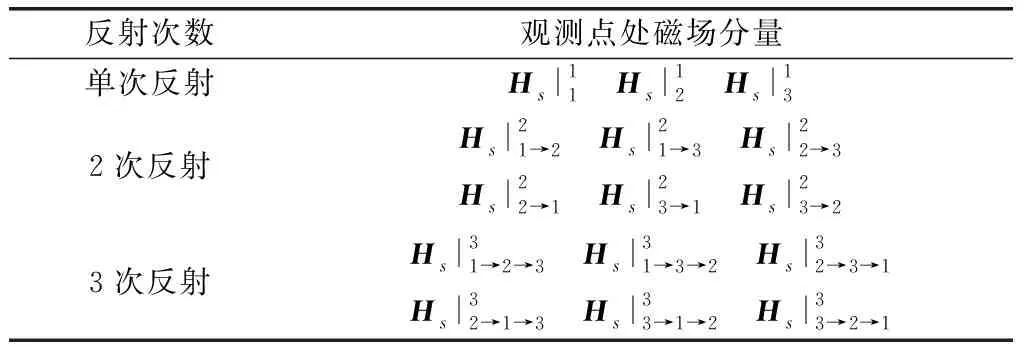
表1 观测点反射磁场的分解

表1的每次反射的贡献可以通过将式(6)～式(8)代入式(2),得到

(9)

(10)

(11)

这里需要明确的是,式(9)～式(11)中积分的区域必须仅在用电磁波照射到的区域上进行。

结合式(9)～式(11),得到观测点总的反射磁场HS为

(12)

根据RCS定义,σ可表示为

(13)

1.3 基于AP的照射区域确定

本文第1.2节通过应用PO法全面、直观地推导出了角反射体全向RCS的计算公式,但由于多次反射时电磁感应过程复杂,如果继续用其确定照射区域(积分区域)将使问题变得非常繁琐。受文献[11]启发,笔者转而利用AP法确定各种反射类型照射区域。鉴于AP法是一种简单、高效的二维投影方法[26-29],其与PO法的联合为后续研究结构更加复杂的角反射体乃至异形角反射体提供了可能性。

基于AP法确定照射区域具体分析如下:首先,考虑单次反射的情形,将与入射波垂直的无限大平面分别投影至各面,其重合区域即为单次反射照射区域,容易发现,除去垂直(θ=0°)和水平(θ=90°)入射2种情形,面1、2、3均被全部照射,即面1、2、3本身即为照射区域面l′,当电磁波垂直入射时,照射区域仅为面1,而电磁波水平入射时,照射区域仅为面2和面3;2次反射在单次反射基础上进行,将单次反射照射区域面l′沿反射波方向向其余2个面投影,其与各面相交部分即为2次反射照射区域面m′;同理,对于3次反射情形,只需把2次反射照射区域面m′沿第2次反射波方向向第3个面投影,投影面与该面本身相交部分即为3次反射照射区域面n′。根据AP法易得到15种反射类型(单次反射3种类型,2次反射和3次反射各6种类型)各自的照射区域。

图2～图4以三面三角形角反射体为例,给出电磁波在φ=30°入射情形下的反射过程及其部分照射区域示意图。其中,S3代表入射波经面3到达观测点情形下,在面3上的照射区域;S31代表入射波按照面3和面1顺序的反射情形下,在面1上的照射区域,S312代表入射波按照面3、面1和面2顺序的反射情形下,在面2上的照射区域。式(14)～式(16)进一步通过计算给出照射区域S3、S31、S312的具体数值大小。三面矩形角反射体及三面圆形角反射体的反射过程及其照射区域可类似获得。

图2 单次反射的照射区域示例(φ=30°) 图3 2次反射的照射区域示例(φ=30°) (S3;入射波→面3→观测点) (S31;入射波→面3→面1→观测点) Fig.2 Example of a single reflection in the irradiated region (φ=30°) Fig.3 Example of the two reflection region (φ=30°) (S3; incident wave→ surface 3→observation point) (S31; incident wave→surface 3→surface 1→observation point)

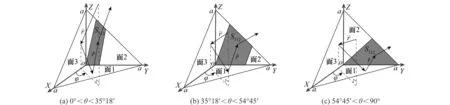
图4 3次反射的照射区域示例(φ=30°) (S312;入射波→面3→面1→面2→观测点)Fig.4 Example of the three reflection region (φ=30°) (S312; incident wave→surface 3→surface 1→surface 2→observation point)

(14)

(15)

S312=

(16)

2 角反射体全向RCS特性分析

为了更加清晰、全面直观地展示三面角反射体全向RCS特性,下文开始对包含角反射体类型及入射波的角度、频率、极化方式、反射次数在内的RCS特性展开详细分析。

2.1 角反射体的全向RCS整体特性分析

首先选取固定方位角φ=45°和φ=60° 2种情形,对PO/AP方法获得的结果进行分析。图5给出了在方位角φ=45°时垂直极化下角反射器的RCS与俯仰角θ的关系示例。横轴表示俯仰角θ,纵轴表示RCS的分贝值,其中0 dB为1 m2。

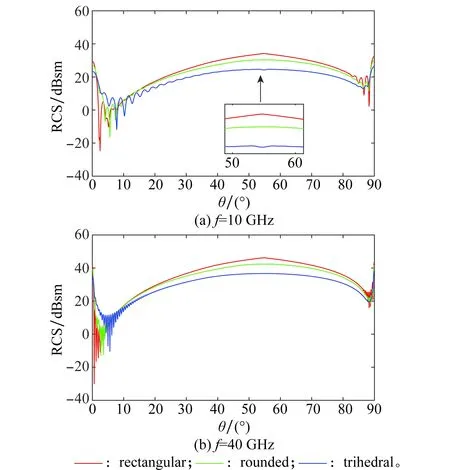
图5 RCS与入射俯仰角θ的关系(φ=45°)Fig.5 Relationship between the RCS and the incidencepitching angle θ(φ=45°)

由图5可知,当入射仰角θ为0°、54.75°和90°时RCS最大,不难看出,它分别由单反射,3次反射和2次反射引起。

在θ=0°和90°附近,RCS存在较大的上下起伏,这是因为随着入射方向远离角反射体的对称轴(θ=54.74°),RCS逐渐由3个面反射作用的效果转变为由1个或2个面反射作用的效果。

出现以上几个最大值的情况如下所示:

(1)在θ=54.74°时,相对于角反射器是对称轴入射,因此,此时的RCS在θ=0°和90°之间具有最大值σmax,Ae=A(A:实际开口面积)。

(2)当俯仰角度θ=90°时,RCS是由面2和面3组成的双面角反射器反射得到的,这相当于用边长为a的二面角反射体在电磁波入射方向投影得到的最大面积作为式(1)中的有效面积求得的值。

(3)当方位角θ=0°时,即面1作为单导体存在时,RCS是由面1对电磁波的反射得到的,这相当于式(1)中的有效面积为边长为a的正方形平板的面积,此时计算结果即为所获得的RCS值。

从这些结果可以看出,这里使用的PO方法可以完美适用于角反射体的分析,随着频率增加,θ=0°和90°附近的图案变得复杂,但是包括最大值主瓣的半值宽度与频率无关,几乎是恒定的。关于这点,本文将在后续进一步讨论。

另外,从式(1)可以看出,RCS的最大值σmax(θ=54.74°)与频率的平方成正比,但是在对称轴入射角度以外的范围并非这样,例如,在θ=0°和90°附近时,10 GHz的RCS局部超过40 GHz的RCS。图6表示方位角φ=60°时角反射体的RCS与入射俯仰角θ的关系。

图6 RCS与入射俯仰角θ的关系(φ=60°)Fig.6 Relationship between the RCS and the incidence pitching angle θ(φ=60°)

由图6可知,与图5相比,由于入射方位角变化,主瓣的最大值减小,而且RCS幅值曲线变得更平坦,主瓣的半值宽度增加,同时与图5相比,最大值的不连续性相比于φ=45°时变得不明确。接下来,当极化方式设定为45°斜极化时,RCS与入射俯仰角θ的关系如图7所示。

图7 RCS与入射俯仰角θ的关系(45°斜极化)Fig.7 Relationship between the RCS and the incidence pitching angle θ (45° diagonal polarization)

与图5对比可见,在θ=90°附近观察到RCS的快速下降,由于在这个角域内,主要表现为双面反射器的散射特性,所以认为两次反射易受极化方式的影响。

进一步改变极化方式,发现在θ=20°以后的图案基本不受影响,也不影响对称轴入射角附近的值,所以可以认为主瓣的半值宽度几乎不受极化方式的影响。

2.2 各次反射模型及其特性分析

接下来,为了得到每种反射对角反射体整体RCS的贡献,分别考虑式(13)分子的每一项计算结果。首先,考虑式(13)分子的第1项所对应的一次反射成分如图8所示。

图8 单次反射对RCS的贡献(φ=45°)Fig.8 Contribution of single reflection to the RCS(φ=45°)

在θ=0°附近,由于出现单面反射器的特性,所以在θ=0°处显示为最大值,RCS随着θ的增加而减小,当θ超过约50°时,认为这是角反射体表面1的1次反射结果和另外2个表面的1次反射的结果的合成。

此时,RCS图案具有许多局部最大点和零点,认为θ<50°时相对规则的主瓣和旁瓣的零点是由于表面1的单次反射造成的结果,此时,入射角θ0为

(17)

从式(17)可以看出,随着频率的增加,旁瓣间隔变窄,呈现出复杂的图形。

在θ>50°处看到的零点被认为是表面1的一次反射和来自表面2和表面3的一次反射的结果合成,此时,入射角θ0为

(18)

接下来,图9给出了2次反射对RCS的贡献,对应于式(13)中分子的第2项。θ=90°的RCS可以被认为是二面角反射器反射得到的结果,转换单位后的平方值与入射波频率平方成正比。其他入射角的RCS具有与一次反射一样最大值间隔变窄的特性。

图9 2次反射对RCS的贡献(φ=45°)Fig.9 Contribution of the two reflection to the RCS(φ=45°)

此外,如图9所示,在θ=54.75°左右时,RCS极度降低并成为零点,这表明电磁波在沿对称轴方向附近入射时被消除了2次反射分量,反映2次反射后总是会接受剩下的一个表面的第3反射。最后,本文对3次反射分量进行分析,如图10所示。

图10 3次反射对RCS的贡献(φ=45°)Fig.10 Contribution of the three reflection to the RCS (φ=45°)

可以看出,3次反射对RCS贡献在10 GHz、20 GHz和40 GHz的频率之间存在6 dB的差异,即3次反射的RCS在整个入射角范围内与入射波频率的平方成比例。但是,包括最大值主瓣的半值宽度却与频率无关,主瓣半值宽度的起始值在θ方向和φ方向分别为22.2°和25.2°。

同时,根据图10所示,发现这种3次反射的RCS图案直接影响3种反射模式合成下的RCS在最大值(入射仰角θ=54.74°)附近的图案(图5),再一次印证了电磁波在沿对称轴角度方向附近入射时,经两次反射后总是会接受剩下的一个面的第3次反射。

3 仿真验证

本节将通过仿真试验,对比PO/AP算法、FEKO(一款三维全波电磁仿真软件)电磁散射仿真软件在角反射体全向RCS上的差异,验证本文所提出的PO/AP算法的有效性。没有特殊说明,以下均采用水平极化方式。

首先,选取FEKO 7.0电磁仿真软件中的弹跳射线法(shooting and bouncing rays,SBR)[30]作为验证工具,对理想金属导体构成的角反射体(a=0.5m)进行仿真,仿真模式为单站反射,仿真环境为f=10 GHz,俯仰角φ∈[0°,90°](步长0.1°),方位角θ∈[0°,90°](步长0.1°),仿真平台为ThinkPad T470、Intel(R) Core(TM) i5-7200U CPU @2.50 GHz 2.71 GHz、16 G内存、NVDIA GeForce 940MX 2 GB显卡。三类角反射体RCS仿真运行时间分别为2.64 h、2.53 h和2.46 h,3D仿真图如图11所示。图12给出了PO/AP算法、FEKO仿真试验结果对比图。

图11 角反射体RCS 3D仿真图(FEKO)Fig.11 3D simulation diagram of RCS corner reflector(FEKO)

图12 PO/AP算法、FEKO仿真试验结果对比(三角形角反射体)Fig.12 Results contrast of PO/AP algorithm and FEKO simulation (triangle corner reflector)

由图12可以看出,由PO/AP算法所得到的角反射体全向RCS与FEKO仿真试验结果具有较好的一致性,很好地验证了PO/AP算法在角反射体全向RCS预估上的有效性。相比于FEKO仿真,算法在相同平台上的运行时间仅为0.865 s、0.851 s和0.846 s,显著提高了角反射体RCS的预估效率。

4 结 论

鉴于角反射体在军事应用中的重要作用,为全面深入掌握角反射体全向RCS特性,针对国内外现有研究现状的不足,提出综合利用PO和AP法的混合算法,构建了基于PO/AP三面角反射体全向RCS模型,并对模型各参数进行了详细分析。FEKO仿真试验验证了本算法的有效性。

由于PO/AP算法全面直观、简洁高效的性质,未来可直接推广应用于结构更加复杂的角反射体乃至异形角反射体的工程设计及其电磁散射特性分析中,具有较大的工程应用及理论价值。

参考文献：

[1] 胡生亮, 罗亚松, 刘忠. 海上多角反射体群雷达散射面积的快速预估算法[J]. 海军工程大学学报, 2012, 24(4): 72-75.

HU S L, LUO Y S, LIU Z. Rapid radar cross section estimation algorithm for marine multi-corner reflectors at sea[J]. Journal of Naval University of Engineering, 2012, 24(4): 72-75.

[2] MIANROODI R Y, HEIDAR H, ARMAKI H M. Expandable shipboard decoy including adequate RCS by using trihedral corner reflectors[J]. IET Science Measurement Technology, 2016, 10(5): 485-491.

[3] BOVENGA F, PASQUARIELLO G, PELLICANI R, et al. Landslide monitoring for risk mitigation by using corner reflector and satellite SAR interferometry: the large landslide of Carlantino (Italy)[J]. Catena, 2017, 151:49-62.

[4] 贺平.雷达对抗原理[M].北京:国防工业出版社,2016:210-214.

HE P. Principle of radar countermeasure[M]. Beijing: National Defense Industry Press, 2016:210-214.

[5] 罗亚松,刘忠,付学智.炮射随机角反射阵列的RCS预估研究[J]. 系统仿真学报, 2009, 21(7): 2077-2080.

LUO Y S, LIU Z, FU X Z. Research on random array of corner reflectors shot by naval guns and RCS estimation[J]. Journal of System Simulation, 2009, 21(7): 2077-2080.

[6] 丁鹭飞.雷达原理[M].北京:电子工业出版社,2014:188-190.

DING L F. Radar Principles[M]. Beijing: Publishing House of Electronics Industry, 2014:188-190.

[7] ABBASI R U, ABE M, OTHMAN M A B, et al. First upper limits on the radar cross section of cosmic-ray induced extensive air showers[J]. Astroparticle Physics, 2017, 87:1-17.

[8] BRANDSEMA M J, NARAYANAN R M, LANZAGORTA M. Theoretical and computational analysis of the quantum radar cross section for simple geometrical targets[J]. Quantum Information Processing, 2017, 16(1):32-35.

[9] 范学满,胡生亮,罗亚松,等.海上角反射体群的RCS快速混合预估算法[J].系统工程与电子技术,2016,38(11):2462-2467.

FAN X M, HU S L, LUO Y S, et al. Hybrid RCS evaluation method for maritime multi-corner reflectors[J]. Systems Engineering and Electronics, 2016, 38(11):2462-2467.

[10] KARAEV V Y, PANFILOVA M A, JIE G. Influence of the type of sea waves on the backscattered radar cross section at medium incidence angles[J]. Izvestiya Atmospheric & Oceanic Physics, 2016, 52(9):904-910.

[11] AHMED S. The study of the radar cross section of perfect electromagnetic conductor strip[J]. Optic-International Journal for Light and Electron Optics, 2015, 126(23): 4191-4194.

[12] YUE K, LIU W, LI G, et al. Numerical simulation of RCS for carrier electronic warfare airplanes[J]. Chinese of Journal Aeronautics, 2015, 28(2):545-555.

[13] 黄坦, 徐振海, 戴崇,等. 隐身目标雷达散射截面最优分布模型选择[J]. 电波科学学报, 2014, 29(5):899-904.

HUANG T, XU Z H, DAI C, et al. Optimal distribution model selection of stealth target RCS[J]. Chinese Journal of Radio Science, 2014, 29(5):899-904.

[14] LI Q, VERNON R J. Theoretical and Experimental investigation of gaussian beam transmission and reflection by a dielectric slab at 110GHz[J]. IEEE Trans.on Antennas & Propagation, 2006, 54(11):3449-3457.

[15] YANG W, KEE C Y, WANG C F. Novel extension of sbr-po method for solving electrically large and complex electromagnetic scattering problem should be a space in half-space[J]. IEEE Trans.on Geoscience & Remote Sensing, 2017, 18(6):1-10.

[16] WENG Y K, LI S, YANG J L, et al. Efficient solution to the RCS of trihedral corner reflector[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 47: 533-539.

[17] ALGAFSH A, INGGS M, MISHRA A K. The effect of perforating the corner reflector on maximum radar cross section[C]∥Proc.of the Microwave Symposium, 2017:1-4.

[18] GROOT J. Letter: cross section computation of trihedral corner reflectors with the geometrical optics approximation[J]. European Trans.on Telecommunications,1992,3(6):637-642.

[19] 范学满, 胡生亮, 贺静波. 一种角反射体雷达散射截面积的高频预估算法[J]. 电波科学学报, 2016, 31(2):331-335.

FAN X M, HU S L, HE J B. High-frequency method for the evaluation of the radar cross section of corner reflectors[J]. Chinese Journal of Radio Science, 2016, 31(2):331-335.

[20] SHAN X J, YIN J Y, YU D L, et al. Analysis of artificial corner reflector’s radar cross section: a physical optics perspective[J]. Arabian Journal of Geosciences, 2013, 6(8): 2755-2765.

[21] JOON T H, SUK Y H, JEE H S, et al. Radar cross section analysis using physical optics and its applications to marine targets[J].Journal of Applied Mathematics and Physics,2015,3(2): 166-171.

[22] JIANG J, LI T, LIU Y. Passive inter-modulation scattering analysis of reflector considering contact nonlinearity[J]. Chinese of Journal Aeronautics, 2013, 26(2):463-469.

[23] 张洪欣, 沈远茂, 韩宇南. 电磁场与电磁波[M]. 北京:清华大学出版社, 2013:250-251.

ZHANG H X, SHEN Y M, HAN Y N. Field and wave electromagnetics[M].Beijing:Tsinghua University Press,2013:250-251.

[24] BARAN A J, HESSE E, SOURDEVAL O. The applicability of physical optics in the millimetre and sub-millimetre spectral region. Part I: the ray tracing with diffraction on facets method[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2017, 190:13-25.

[25] GAO M, YANG F, YAN F, et al. An efficient method for calculation the physical optics integral by using complex source beam for electrically large reflector antenna applications[J]. Electromagnetics, 2017, 37(1):17-26.

[26] CHENG D K. Field and wave electromagnetics: pearson new international edition[M]. Pearson Schweiz Ag, 2013.

[27] LIANG J, HOU Z, CHEN C, et al. Supervised bilateral two-dimensional locality preserving projection algorithm based on gabor wavelet[J].Signal Image & Video Processing,2016,10(8):1-8.

[28] CHUPIN L, DUBOIS T. A bi-projection method for Bingham type flows[J]. Computers & Mathematics With Applications, 2016，72(5): 1263-1286.

[29] AREVALILLO-HERREZ M, GDEISAT M, LILLEY F, et al. A spatial algorithm to reduce phase wraps from two dimensional signals in fringe projection profilometry[J]. Optics & Lasers in Engineering, 2016, 82:70-78.

[30] 邓泳,董纯柱,耿方志.一种计算电大尺寸复杂导体目标电磁散射的Mom-SBR/PO混合法[J].系统工程与电子技术,2009,31(6): 1400-1403.

DENG Y, DONG C Z, GENG F Z. Hybridization of Mom-SBR/PO for computing electromagnetic scattering of electrical large-size complex conducting bodies[J]. Systems Engineering and Electronic, 2009, 31(6): 1400-1403.