舰船舱内爆炸载荷特征与板架毁伤规律分析

姚熊亮，屈子悦，姜子飞，王志凯，王治

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

0 引 言

水面舰船在现代海战中发挥着重大作用，舰船抗爆抗冲击性能和舰船生命力研究一直备受各国关注。水下近场、远场爆炸，以及空中爆炸、空中核爆炸均会对水面舰船的生命力造成威胁。研究海上反舰武器对舰船生命力的毁伤规律对于提高我国海军作战能力具有重要指导意义。

近年来，国内外众多学者对舰船抗爆抗冲击性能进行了大量研究，尤其是空中爆炸载荷作用下舰船结构的毁伤情况。杨棣等［1］将船体板架结构简化为交叉梁系结构，提出了接触爆炸作用下塑性区与破口大小的预估公式。周姝［2］模拟了不同舱室及板架空中爆炸、不同装药密度W/V（W为药量，V为舱室体积）下货舱舱室的内爆工况，以及某船舱室与缩比舱室内爆的对比工况，得出了内爆载荷特性与板架变形规律。Du等［3］模拟了空中内爆作用下舰船舷侧防护结构的损伤情况，分析了爆炸冲击波在舱室内的传播规律。Baker［4］对大量爆炸试验数据予以了总结，并将其汇编成了一系列规范的表格。张振华和朱锡［5］对刚、塑性板在柱状炸药接触爆炸载荷作用下的破口开裂情况进行了研究。但在前人的研究中，针对不同形式舱室内爆载荷传播特性以及板架毁伤规律的研究还比较少。

为此，本文拟建立密闭舱室与开口舱室模型，在不同药量情况下模拟自由场爆炸与舱室内爆，并将数值计算载荷与亨利奇公式计算结果进行对比，分析炸药在密闭舱室以及开口舱室内的爆炸过程，从而对不同舱室情况下的载荷特性以及结构毁伤规律进行分析。

1 有限元数值模拟计算

参考不同舰船舱室的一般结构，采用某典型舱室的尺寸建立有限元模型。本文采用ANSYS软件建模，用LS-DYNA模拟爆炸和舱室结构毁伤结果。舱内爆炸三维有限元模型主要包括舱室结构有限元模型、空气流场有限元模型和炸药有限元模型3种，其中空气流场有限元模型和炸药有限元模型是直接在ANSYS中建立2个球体单元，然后各自赋予属性和状态方程，进而对爆炸进行模拟。

1.1 结构与炸药材料特性

1）结构材料特性。

考虑材料应变率敏感性的本构方程很多，本文采用与实验数据吻合较好的Cowper-Symonds模型来描述材料的应变率效应。动态屈服强度σd为

式中：σ0为屈服极限；E为杨式模量；ET为切线硬化模量；εp为有效塑性应变；εd为等效塑性应变；D，δ为应变率参数。

材料相关参数如表1所示。

表1 钢材料模型参数Table 1 Model parameters of steel material

结构产生破口与否与失效应变的选取密切相关，不同材料其失效应变不同，当材料产生的应变大于材料失效应变时，材料开始产生断裂，即结构出现破口。对于船用钢材，通常取失效应变为0.3，0.28和0.21等，鉴于本模型所使用钢材的屈服极限较高，故取失效应变为0.3，亦即如果结构的等效塑性应变大于0.3，则结构出现破口。

2）流场材料特性。

本文采用流体常用模型MAT_null模拟流场本构关系，空气状态方程采用EOS_linear_polynormal方程，相关参数如表2所示。表中，C0～C6为方程系数。

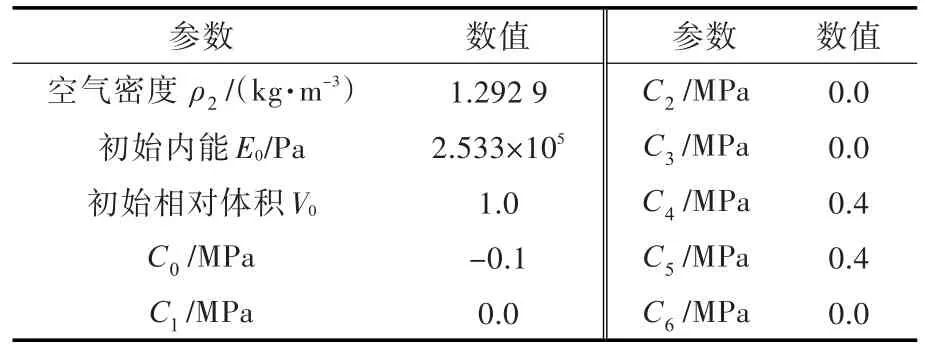
表2 流场状态方程参数Table 2 Flow field state equation parameters

线性多项式状态方程如式（2）所示：

式中：P为爆轰压力；E′为当前内能；ζ为当前密度与初始密度之比。

3）炸药状态方程。

对于TNT炸药，采用JWL状态方程：

式中：V为当前相对体积；A1，A2，r1和r2为常数；ω为比热。各参数的取值如表3所示。

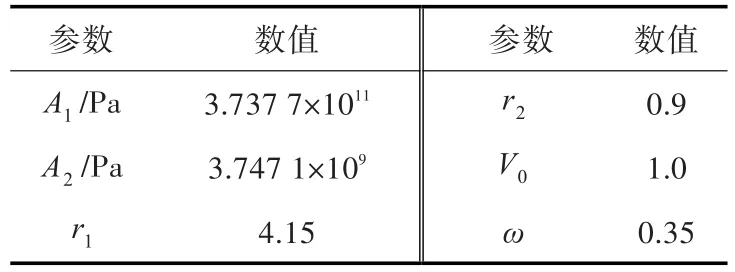
表3 JWL状态方程参数Table 3 JWL state equation parameters

1.2 结构模型与工况

为分析舱内爆炸作用下舱室结构的毁伤情况，并与舱壁上有泄爆孔的舱室进行对比，本文建立了2种舱室结构：密闭舱室和开口舱室。依照某舰船典型舱室结构尺寸，设置这2种舱室的长、宽、高均为5 m×5 m×3 m，其中密闭舱室四周舱壁密闭，开口舱室四周舱壁有1.2 m×0.6 m的开口。舱室结构均采用四边形壳单元模拟，壁厚10 mm，舱壁上有T型加强筋。2种舱室结构如图1所示。

本文采用欧拉网格模拟炸药与空气，爆炸模型示意图如图2所示。

球形装药位于结构中心，根据药量求出药包半径。空气流场半径5 m。为研究不同药量对舱内冲击波与板架毁伤的影响，依据舱室内爆的常用药量，选取药量为30和150 kg TNT。

1.3 舱内冲击波超压计算

载荷是一切物理过程计算的基础，只有载荷输入正确，才能保证计算结果精确。文献［2］经过对比分析发现亨利奇公式是以大量的试验为基础，故其使用范围较广，可信度高。本文将有限元软件计算的爆炸冲击波超压峰值与亨利奇公式计算的结果进行了对比，保证了载荷的准确性。亨利奇公式如下所示［6］。

式中：ΔPf为冲击波峰值超压；为相对距离，其中R为爆距，Q为爆炸当量。

由于药包与结构的最小距离为1.5 m，根据式（3），可以求出药量为30和150 kg时空气自由场中距药包1.5 m处的超压峰值分别为2.9与10.2 MPa。测出的空气自由场中距药包1.5 m处单元的压力时历曲线见图3，其超压值与理论值接近，可以认为有限元模型对空爆的模拟较为可信。

2 计算结果分析

2.1 不同舱室载荷对比分析

舱室内爆载荷主要由动压和爆轰产物膨胀产生的准静态压力组成。舱内爆炸载荷会受到舱室结构形式的影响，密闭舱室与开口舱室舱壁受到的爆炸载荷有所区别。为研究冲击波载荷规律，选取密闭舱室与开口舱室的相同位置（顶部舱壁中心点）处为测点，分析舱壁测点处承受的载荷情况。

图4所示为不同药量下密闭舱室与开口舱室测点处压力随时间变化的曲线图。从图中可以看出，舱壁上的冲击波出现了多个峰值，冲击波到达舱壁后形成反射，反射冲击波逐次减弱；密闭舱室与开口舱室的初始冲击波压力峰值大致相同，即表示该峰值为最大冲击波压力峰值；开口舱室的前2次反射冲击波峰值比密闭舱室的前2次反射冲击波峰值小。

由图得知，密闭舱室与开口舱室冲击波冲量的差异主要存在于反射波与准静态压力阶段。经计算，当药量为30 kg TNT时，开口舱室冲击波的总冲量约为密闭舱室的22.63%；当药量为150 kg TNT时，开口舱室冲击波的总冲量约为密闭舱室的55.75%；可见，与30 kg TNT工况相比，当药量为150 kg TNT时，2种舱室内的冲击波冲量相差较小，这可能是因为密闭舱室角隅处发生了撕裂，起到了一定的泄压作用。

在t=50 ms以后，舱室内爆有一段相当长的压力振荡阶段，这个阶段即为准静态峰值压力衰减阶段，该阶段不会存在于自由场爆炸中。由于开口舱室起到了很好的泄压作用，故密闭舱室的准静态压力明显大于开口舱室的准静态压力。

2.2 载荷传播特性分析

以30 kg TNT药量为例，给出了冲击波传播云图。图5所示为30 kg药量时舱室内爆冲击波随时间变化的云图。从图中可以看出，冲击波是从舱室中间区域传播至角隅区域。在t=60 ms时，密闭舱室角隅处仍汇集有压力而开口舱室则不明显。

密闭舱室内爆冲击波载荷会汇聚于角隅处。为充分研究冲击波载荷规律，现以密闭舱室为例进行载荷特性分析。在舱室的上甲板布置测点，测点布置如图6所示。

在板架上建立一个直角坐标系，坐标原点位于板架中央，以板架长L=5 m方向为X轴，板架宽B=5 m方向为Y轴，测点1位于板架中心，测点4位于角隅处。具体位置如表4所示。

表4 板架测点位置表Table 4 Coordinates of gauging point at stiffened plate

图7所示为在30 kg TNT药量下，密闭舱室内爆板架4个测点处的压力时历曲线。由图可以看出，由于结构密闭，板架上出现多个冲击波压力峰值［7-8］，其中最大冲击波压力峰值出现在板架中心测点1处。最大冲击波压力峰值排序为：测点1＞测点2＞测点3＞测点4，冲击波压力峰值到达的时间为t1＜t2＜t3＜t4。约在t=7 ms后，测点4处的压力持续增加并保持在约1 MPa状态下，这说明测点4所在的角隅处产生了汇聚冲击波。在t=23 ms后，舱内冲击波开始持续震荡，这个阶段即为准静态压力峰值衰减阶段。

表5给出了4个测点处的冲击波总冲量值。测点1处的初始冲击波峰值虽然最大，但冲击波总冲量最小，由此可知，反射冲击波与准静态压力值占总冲量的主要部分。测点4位于角隅处，此处的冲击波总冲量值最大，约为测点1处的1.45倍，进一步验证了冲击波在角隅处汇聚的现象。

表5 测点处的冲击波总冲量值Table 5 Total impulse values of the shock wave at gauging points

2.3 结构毁伤规律分析

在舱室内爆载荷的作用下，舱室板架结构会受到壁面反射冲击波和角隅汇聚冲击波的反复作用，以及准静态压力的作用。在壁面反射冲击波的作用下，随着载荷的增强，舱室板架结构有2种失效模式：局部塑性变形和撕裂失效。其中，局部塑性变形又可以分为局部凸起塑性变形和面板沿加强筋发生颈缩；撕裂失效可以分为沿加强筋发生部分撕裂、完全撕裂以及加强筋断裂［9］。

图8所示为30 kg TNT药量时舱室结构应变随时间变化的云图。从图中可以看出，在t=1.5 ms左右时，密闭舱室距离炸药最近的舱壁顶板中央最先开始发生变形；冲击波在发生壁面反射后，开始向角隅传播，使角隅部分产生了塑性变形；由于药量较小、舱壁板较厚，舱壁沿加强筋虽然发生了塑性变形，但未产生破口与撕裂失效。与密闭舱室不同的是，开口舱室由于开口的泄压作用，角隅处并没有产生明显的塑性变形，但开口附近产生了轻微的塑性变形［10-11］。

图9所示为150 kg TNT药量时舱室结构应变随时间变化的云图。从图中可以看出，密闭舱室距离炸药最近的舱壁顶板中央最先开始发生变形；随着冲击波的多次反射，角隅处产生了塑性变形；冲击波在角隅处的汇聚使舱壁间角隅部位迅速撕裂；壁面反射冲击波使舱壁沿加强筋发生了塑性变形。与密闭舱室不同的是，开口舱室舱壁间角隅处没有发生撕裂，压力通过开口耗散使得开口处发生了外翻。

表6以2.2节中舱室上甲板上的4个测点为研究对象，给出了不同药量下开口舱室与密闭舱室上甲板测点处的塑性变形值（单位：mm）与变形差值百分比。由表可知，在30 kg TNT药量下，开口舱室与密闭舱室相比，由于开口的泄压作用，使得测点处的塑性变形值下降，两者差所占百分比在25%以上；在150 kg TNT药量下，开口舱室测点处的塑性变形值虽然较密闭舱室测点处的塑性变形值有所下降，但两者间的差值较小，差值所占百分比在15%以下，其原因是密闭舱室角隅处的撕裂起到了一定的泄压作用，从而使得其变形结果与开口舱室相比相差较小。

依据简化理论公式，计算板架中心最大变形与数值模拟结果，并进行比较。为了探究准静态压力的影响，分别对只考虑冲击波以及冲击波与准静态压力联合作用这2种板架中心变形进行了比较。

表6 舱室上甲板塑性变形值Table 6 Plastic deformation values of upper deck of cabin

考虑准静态压力的板架中心位移简化公式如式（5）所示：

式中：W0为板架中心最大位移，m；A，B，C，G，U为系数，其值可以通过下式求得：

式中：h为板厚，m；a为板架长边的一半，m；b为板架短边的一半，m；n为与板架长边垂直的加筋数量；m为与板架短边垂直的加筋数量；K为动载荷系数；σs为板架材料屈服应力，Pa；xi为与板架长边垂直的第i根加筋的x坐标，m；yj为与板架短边垂直的第j根加筋的y坐标，m；Mas为与板架长边垂直的加筋全塑性弯矩，N·m；Mbs为与板架短边垂直的加筋全塑性弯矩，N·m；PQ为板架所受准静态压力载荷峰值，Pa。

只考虑冲击波对舰船板架的影响时，根据能量原理，有

式中，ke为冲击波动能，计算公式如下：

式中：i为冲击波冲量；ρp为材料密度；ΔPm为冲击波峰值；W为位移；t+为冲击波正压作用时间；T为板架自振周期。通过对板架进行模态分析，得到舱室上甲板自振周期T=40 ms，30和150 kg TNT药量下的冲击波正压作用时间分别为1.2和1.5 ms，所以，

简化计算方法，分为考虑准静态压力部分与只考虑冲击波冲击2种情况，并与数值计算中准静态压力产生前、后的结果进行对比［12-13］，计算结果如表7和表8所示。

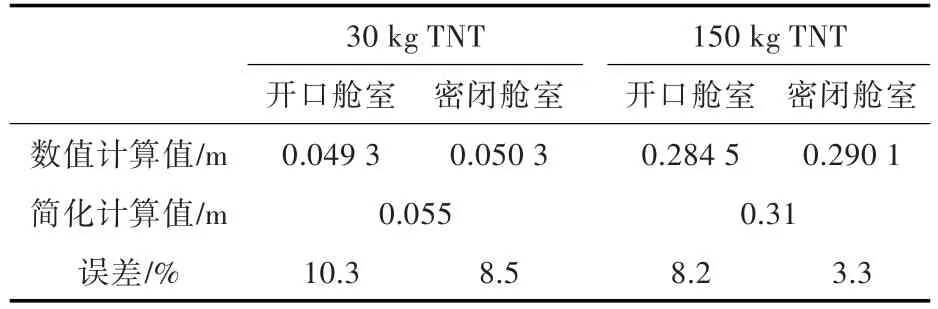
表7 板架中心变形值对比表（只考虑冲击波影响）Table 7 Deformation values at stiffened plate center（only shock waves considered）

表8 板架中心变形值对比表（冲击波与准静态压力联合作用）Table 8 Deformation valuesatstiffened plate center（combined effect of shock wave and quasi-static pressure）

由表7、表8可知，只考虑冲击波的影响时，数值计算结果与简化计算方法所得结果间误差较小，控制在10%左右；考虑准静态压力影响时，误差较大，其原因可能是因为进行数值模拟计算时静态压力是一个衰减的过程，而简化计算方法是受准静态压力峰值的影响，不用考虑其衰减过程。另外，30 kg TNT药量属于小当量，舱室内爆轰气体所占比例很小，其所产生的准静态压力相对于爆炸冲击波压力很小，所以舱内准静态压力影响不明显，与理论值相比差别较大。

3 结 论

本文通过数值计算，模拟了自由场、密闭舱室以及开口舱室内的爆炸载荷，并进行对比分析，得到了30和150 kg TNT药量作用下开口舱室与密闭舱室的毁伤规律，并就其毁伤模式进行了分析。得到以下主要结论：

1）密闭舱室与开口舱室内的爆炸冲击波载荷不同，两者与自由场中的爆炸冲击波载荷也有很大的区别，但两者的初始冲击波压力峰值与自由场冲击波压力峰值大致相同。

2）冲击波到达舱室壁面后形成反射冲击波，出现多个逐次减弱的反射压力峰值，随后，出现准静态压力阶段。与密闭舱室相比，开口舱室的反射压力峰值小，且在密闭舱室未破损的情况下，开口舱室的冲击波总冲量约为密闭舱室的20%。

3）冲击波在舱室角隅处汇集，角隅处的冲击波总冲量约为板架中心处冲击波总冲量的1.45倍。

4）密闭舱室板架的失效模式为板架沿加强筋发生塑性应变和沿角隅发生撕裂；开口舱室由于开口的泄压作用，角隅处并未发生撕裂，但开口边缘处发生了外翻变形。

5）只考虑冲击波的影响时，采用数值模拟法计算板架中心最大变形与简化计算方法相比误差较小，约为10%；而考虑准静态压力作用时，采用数值模拟法计算板架中心最大变形与简化计算方法相比误差较大。

［1］杨棣，姚熊亮，王军，等.接触爆炸载荷作用下船体板架破口大小的预测［J］. 中国造船，2014，55（2）：77-84.YANG D，YAO X L，WANG J，et al.Forecast of crevasse size of hull grillage in contact explosion［J］.ShipbuildingofChina，2014，55（2）：77-84（inChinese）.

［2］周姝.空爆载荷作用下舱室结构毁伤计算方法研究［D］.哈尔滨：哈尔滨工程大学，2014.

［3］DU Z P，LI X B，XIA L J，et al.Numerical simulation of warship broadside protective structure rupture under inner explosion［J］.Journal of Ship Mechanics，2007，11（3）：453-461.

［4］BAKER W E.Explosions in air［M］.Austin：University of Texas Press，1973.

［5］张振华，朱锡.刚塑性板在柱状炸药接触爆炸载荷作用下的花瓣开裂研究［J］. 船舶力学，2004，8（5）：113-119.ZHANG Z H，ZHU X.Petaling of rigid plastic plate under contact explosive loading of cylindrical dynamite［J］.Journal of Ship Mechanics，2004，8（5）：113-119（in Chinese）.

［6］亨利奇.爆炸动力学及其应用［M］.熊建国，译.北京：中国科学技术大学出版社，1987.

［7］汪维，张舵，卢芳云，等.大当量TNT装药爆轰的远场数值模拟及超压预测［J］.弹箭与制导学报，2010，30（1）：127-130.WANG W，ZHANG D，LU F Y，et al.Simulation of thousands kilograms of TNT explosion shock wave in air at distance far away and forecast of the peak overpressure［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30（1）：127-130（in Chinese）.

［8］张舵，吴克刚，卢芳云.建筑物内爆炸波的动压载荷研究［J］. 采矿技术，2009，9（5）：68-72，79.ZHANG D，WU K G，LU F Y.Research on dynamic pressure load under interns blast［J］.Mining Technology，2009，9（5）：68-72，79（in Chinese）.

［9］侯海量，朱锡，梅志远.舱内爆炸载荷及舱室板架结构的失效模式分析［J］. 爆炸与冲击，2007，27（2）：151-158.HOU H L，ZHU X，MEI Z Y.Study on the blast load and failure mode of ship structure subject to internal explosion［J］.Explosion and Shock Waves，2007，27（2）：151-158（in Chinese）.

［10］杨棣.水下爆炸下舰艇典型结构塑性损伤研究［D］.哈尔滨：哈尔滨工程大学，2015.

［11］张阿漫，王诗平，汪玉，等.水下爆炸对舰船结构损伤特征研究综述［J］.中国舰船研究，2011，6（3）：1-7.ZHANG A M，WANG S P，WANG Y，et al.Advances in the research of characteristics of warship structural damage due to underwater explosion［J］.Chinese JournalofShipResearch，2011，6（3）：1-7（inChinese）.

［12］WANG A J.The permanent deflection of a plastic plate under blast loading［J］.Journal of Applied Mechanics，1995，22：375-376.

［13］JONES H.Finite deflections of a simply supported rigid-plastic annular plate loaded dynamically［J］.International Journal of Solids and Structures，1968，4（6）：593-603.