反舰导弹战斗部近距空爆的毁伤威胁性分析

赵传，王树山，马瑾，谭朝明

1北京理工大学爆炸科学与技术国家重点实验室，北京100081

2中国船舶工业集团公司系统工程研究院，北京100036

0 引 言

舰载近程反导舰炮武器系统是水面舰艇防空反导作战体系的核心组成部分，担负着“最后一道防线”的作战任务。小口径舰炮对反舰导弹的毁伤效果主要有2种典型模式：一是造成目标在空中解体，战斗部被引爆；二是破坏目标的气动外形或制导控制系统，使其偏航入水从而丧失或大幅减小威胁性。然而，对于小口径舰炮的近距拦截来说，反舰导弹战斗部被引爆所产生的破片、爆炸冲击波等毁伤元素是否会对舰艇造成毁伤，以及战斗部空中爆炸对舰艇的毁伤威胁距离，一直是备受关注和悬而未决的问题［1］。张庆明等［2］分析了反辐射导弹战斗部的结构和性能，建立了其空爆的威力场模型。汪德武等［3］针对一种空爆型杀爆战斗部，提出了战斗部杀伤概率的工程计算方法。许勇等［4］提出了反辐射导弹空爆对航母舰面雷达的毁伤效能评估方法。然而，在建立反舰导弹战斗部空爆威力场，以及空爆产生的破片和冲击波对舰艇的毁伤效应等方面，目前鲜有研究。

针对“捕鲸叉”反舰导弹战斗部空爆对舰艇的毁伤效应问题，本文拟应用毁伤与终点效应学的理论方法建立“捕鲸叉”反舰导弹战斗部的空爆威力场模型，建立大型水面舰艇典型结构、舰面人员、舰载机和其他技术装备的目标等效靶模型。通过对比不同炸点距离下战斗部空爆威力场的作用情况，分析“捕鲸叉”反舰导弹战斗部空中爆炸对舰艇的毁伤威胁距离，用以为武器总体相关领域的研究提供依据和技术支撑。

1 研究对象及基本假设

1.1 典型反舰导弹战斗部

目前，“捕鲸叉”反舰导弹是海军应用最为广泛的亚音速反舰导弹［5］，本文将选择其战斗部作为研究对象。“捕鲸叉”反舰导弹战斗部的结构及尺寸如图1（a）所示，其总重量约230 kg，其中：壳体材料为D6AC钢，质量为130 kg；主装药为 PBXC-129，质量为90 kg，装药密度为1.707 g/cm3，爆速为8 600 m/s，爆热为5 300 kJ/kg，格尼常数为2 928 m/s。

1.2 大型水面舰艇的典型结构模型

图1（b）所示为大型水面舰艇模型的典型外形及尺寸。考虑到反舰导弹战斗部空爆产生的毁伤元、舰艇总体结构特征及其易损性，将从以下4个方面考虑舰艇的毁伤效应：

1）舰艇结构，主要考虑甲板和舷侧。

2）舰载固定翼飞机。

3）舰面技术装备，主要分为2类：一类是不带装甲防护结构的设备，例如雷达、干扰弹发生器等；另一类是带轻型装甲防护结构的设备，例如舰炮等。

4）作战人员。

1.3 基本假设

在本文中，进行如下假设：

1）炸点距离：战斗部炸点距离舰艇目标50～500 m。

2）反舰导弹的瞄准点为舰艇水线以上舷侧的几何中心。

3）反舰导弹战斗部的末段飞行速度为0.85 Mach。

4）不考虑攻角及弹体自转，弹轴与水平面之间呈20°夹角。

5）反舰导弹战斗部为端部起爆，爆轰波阵面的传播方向与弹体运动方向一致。

6）建立破片飞散模型时，仅考虑战斗部壳体产生的前向及侧向破片，忽略战斗部的后向破片以及反舰导弹其他舱段可能产生的破片。

7）采用“炸点距离”描述反舰导弹战斗部炸点与舰艇目标的相对位置，“炸点距离”的含义如图2所示。

2 “捕鲸叉”反舰导弹战斗部的空爆威力场模型

2.1 爆炸冲击波

反舰导弹空爆时主要产生爆炸冲击波和破片这2个毁伤元素，其中爆炸冲击波会对人员、雷达和其他设备的整体结构造成毁伤，其毁伤效果主要取决于峰值超压。目前，爆炸冲击波峰值超压的计算方法已非常成熟，其中针对TNT炸药的经典计算公式为［6］

式中：Δp+为峰值超压，MPa；，为对比距离，其中r为目标与炸点的距离，m，ω为装药TNT当量，kg。

对于其他类型的炸药，可以根据爆热相似原理将实际装药量换算成TNT爆炸的装药量。同时，还需考虑爆炸过程中形成破片损失的能量以及战斗部运动所增加的动能，因此战斗部的实际装药量为

式中：ωe为实际装药的等效TNT当量，kg；QPBX为实际装药的爆热，kJ/kg；QTNT为TNT爆热，kJ/kg；ωi为实际装药质量，kg；ωbe为带壳装药相当于裸装药的当量，kg；a为装填系数，即装药质量与战斗部总质量之比；va为战斗部爆炸的瞬时速度，m/s。

将“捕鲸叉”反舰导弹战斗部的相关参数代入式（2）～式（4），即可得到战斗部产生爆炸冲击波的TNT当量ω=47 kg。

2.2 破 片

破片毁伤元的毁伤能力决定于其特性参数，包括破片数量、破片速度、破片质量分布和空间分布等。

2.2.1 破片质量分布

“捕鲸叉”反舰导弹战斗部在爆炸过程中产生的破片为自然破片，其质量分布受装药种类、壳体力学性能、弹体几何尺寸、装药与壳体匹配关系等多个因素的影响，目前尚无可以准确计算破片质量分布情况的通用模型。为了分析“捕鲸叉”反舰导弹战斗部的破片数量随质量分布的情况，本文开展了缩尺战斗部的弹体破碎性试验。其中实体战斗部与缩尺战斗部的相似比λ=3∶1，试验情况如图3所示。

将2发缩尺战斗部破碎性试验的结果取算数平均值，即为“捕鲸叉”反舰导弹缩尺战斗部的破片质量分布。常用的质量分布模型为Mott分布［7］和Weibull分布［8］，本文将分别采用这2种分布模型对试验结果进行拟合，结果如图4所示。其中：Mott分布的特征质量μ=0.083，拟合相似度R2=0.955；Weibull分布的特征质量μ=0.084，碎裂品质参数Λ=0.408，拟合相似度R2=0.984。

由图4可知，Weibull分布的拟合相似度比Mott分布的高，故选择Weibull分布作为“捕鲸叉”反舰导弹缩尺战斗部的破片质量分布。

参数μ的物理含义是描述破片的平均质量特征，因此μ的影响因素函数为

式中：ρe为装药密度；me为装药质量，ρs为壳体密度；De为主装药爆速；σb为壳体强度极限；δs为壳体厚度；ls为壳体长度；ds为壳体外径。

将ρe，me，De作为独立变量，将式（5）无量纲化，得

缩尺战斗部与原战斗部相比并没有改变主装药种类和壳体材料，故式（6）可以简化为

由式（7）可知，缩尺战斗部的弹体破碎性试验得到的特征质量与实体战斗部的特征质量相比，其结果符合几何相似原理。

参数Λ的物理含义是描述壳体碎裂的均匀性，壳体碎裂越均匀，Λ值越大。Λ取值的影响因素主要包括主装药爆轰参数、壳体力学性能、装填比与装药和壳体的匹配关系。由于相似性试验并没有改变上述影响因素，因此参数Λ的取值不变。

根据相似性试验的几何相似原理，将缩尺战斗部试验得到的Weibull分布参数μ和Λ变换为原战斗部的分布参数：Λ原=Λ=0.408。因此，“捕鲸叉”反舰导弹战斗部的破片质量分布模型为

式中：N(mf)为质量大于mf的破片数量，其中mf为破片质量；M为壳体总质量，g。

根据式（8），计算得到“捕鲸叉”反舰导弹战斗部的破片质量分布如表1所示，其中破片总数N0=11 781，破片的平均质量为10.49 g。

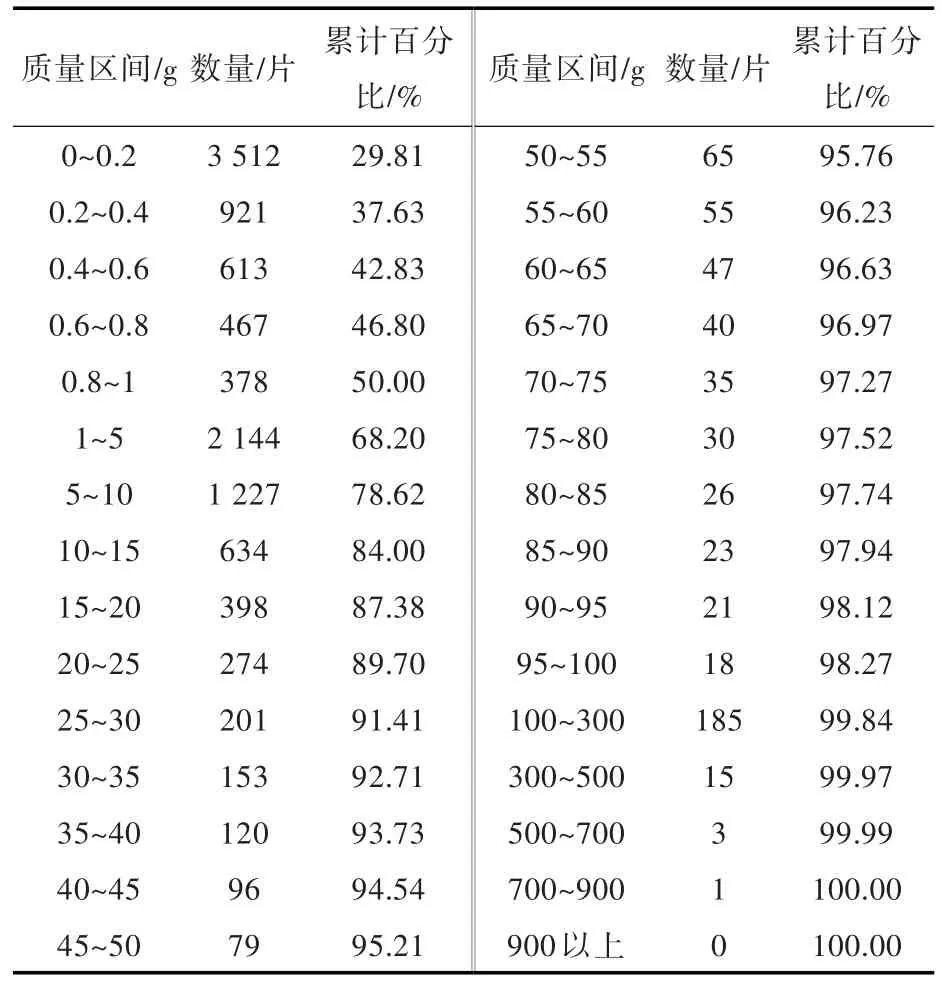
表1 破片质量分布Table1 Fragmentation mass distribution

2.2.2 破片速度

在爆轰产物的驱动下，破片获得的初速度v0通常采用Gurney公式计算［5］

式中：为炸药的Gurney能量；β为主装药质量与壳体质量之比。

考虑战斗部爆炸时的瞬时速度va，则破片的实际初速度vm（单位：m/s）为

经计算，“捕鲸叉”反舰导弹破片的平均实际初速度为2 181.2 m/s。

破片在空气中飞行时，空气阻力会造成其速度衰减，因此破片着靶时的实际速度vf为

式中：R为破片着靶前的飞行距离，m；α为速度衰减系数。

式中：CD为气动阻力系数，对于不规则破片，一般取值1.5；ρa为空气密度，海平面附近的空气密度为1.226 kg/m3；S为破片迎风面积，

式中：H为修正系数，一般取值1.12；ϕ为形状系数，长方形破片一般取值3.8×10-3。

将破片的平均质量mf=10.49 g代入式（12），得α=0.02。

2.2.3 空间分布

对于破片的空间分布模型，采用Shapiro公式即可得到每一枚破片的飞散方向［6］

式中：θs为破片偏转角，即破片运动方向与壳体外法线方向的夹角；φ1为战斗部壳体的法线方向与战斗部对称轴方向的夹角；φ2为爆轰波阵面法线方向与战斗部对称轴方向的夹角。

根据式（14）统计每一枚破片的飞散方向，即可得到图5所示的破片场空间分布。

3 毁伤载荷对舰艇的作用模型

3.1 作用模型

3.1.1 爆炸冲击波

爆炸冲击波毁伤元对舰艇目标的毁伤情况与战斗部炸点和舰艇各目标之间的距离有关，作用模型如图6所示。

3.1.2 破 片

破片毁伤元对舰艇目标的毁伤情况受战斗部姿态、战斗部与舰艇的相对位置、战斗部爆炸瞬间的弹体速度等多个因素的影响。因此，本文建立了破片毁伤元对舰艇目标的作用模型。

1）战斗部坐标系。

omxmymzm战斗部坐标系如图7所示，并在omxmym平面内建立“捕鲸叉”反舰导弹战斗部截面模型：设战斗部炸点为坐标原点om，对称轴为xm轴，战斗部直径方向为ym轴。

将壳体均匀离散，每一枚破片的坐标为Pmi=(xmi，ymi，0)。将每一枚破片的位置Pmi代入式（14）即可得到每枚破片的偏转角θsi，代入式（10）即可得到破片的初速度vmi=(vmisinθsi，vmicosθsi， 0) 。

以xm轴为旋转轴，将战斗部截面进行n次旋转变换，每次转角为N×ξ，其中：N=1，2，3，…，n；ξ为相邻两次旋转变换之间的夹角。为保证破片总数N0=11 781，n和ξ必须选择合适的数值。

每枚破片位置坐标Pmi为

每枚破片的速度向量vmi为

2）舰艇目标坐标系。

以舷侧几何中心为坐标原点o，舷侧法线方向为x轴，舷侧纵向为y轴，舷侧垂向为z轴，建立舰艇目标坐标系，如图8所示。

舷侧方程为：

甲板方程为：

3）破片场命中舰艇模型。

输入战斗部炸点在舰艇目标坐标系中的位置（a，b，c），将战斗部坐标系进行平移变换，本文所示的算例中b=0；输入战斗部在舰艇坐标系中的高低角θ′，将战斗部坐标系绕ym轴进行旋转变换；输入战斗部在舰艇坐标系中的方位角φ′，将战斗部坐标系绕zm轴进行旋转变换。

战斗部壳体每一枚破片在战斗部坐标系中的位置坐标为（xmi，ymi，zmi)，在舰艇目标坐标系中的位置坐标Pi为

战斗部壳体每一枚破片在战斗部坐标系中的速度向量为 (vxmi，vymi，vzmi)，在舰艇目标坐标系中的速度向量vi为

结合式（19）和式（20），可以得到每枚破片在舰艇目标坐标系中的迹线方程为

毁伤载荷对舰艇的作用如图9所示。

4）命中破片数量及平均存速。

联立式（15），式（17）～式（19）即可求解命中舷侧和甲板的破片位置坐标，通过统计坐标数量即可得到命中舷侧的破片数量N侧和命中甲板的破片数量N甲。对于命中舷侧的破片，根据式（8）可得质量大于mf的破片数量的数学期望N侧（mf）为

对于命中甲板的破片，其质量大于mf的破片数量的数学期望N甲(mf)为

根据式（22）和式（23），取不同的mf即可得到破片命中舷侧和甲板时各质量区间内破片数量的数学期望。

根据每一枚破片的命中位置坐标与该破片在战斗部时的原位置坐标，即可求得破片的飞行距离，代入式（11），可以得到破片命中目标时的存速。将命中同一目标的所有破片存速取算数平均值，即可得到命中该目标的破片的平均存速。

3.2 计算结果

3.2.1 爆炸冲击波

不同炸点距离处，反舰导弹战斗部的爆炸冲击波在不同目标处产生的峰值超压如表2所示。

表2 炸点距离目标不同位置处爆炸冲击波的峰值超压Table 2 The peak value of the blast wave at the different positions of the target

3.2.2 破 片

随着炸点距离不同，破片场对舰艇的典型作用情况如图10所示。由图10可以看出，在计算的炸点距离范围内，只有战斗部的前向破片可以命中舰艇，而侧向破片则不能命中舰艇。

在不同的炸点距离，能够命中舰艇的破片数量及平均存速如表3所示。由表3可知，当炸点距离不大于100 m时，前向破片只能命中舷侧而不能命中甲板；当炸点距离不小于150 m时，舷侧和甲板均有前向破片命中。

4 毁伤效应计算与分析

4.1 爆炸冲击波毁伤效应

在本文考虑的炸点距离内，空气爆炸冲击波载荷不会对舰艇甲板和舷侧造成毁伤。爆炸冲击波载荷对舰面目标的毁伤判据和毁伤威胁距离如表4所示［9-10］，其中 ΔP+为爆炸冲击波的峰值超压。当爆炸冲击波在各目标处产生的峰值超压大于或等于ΔP+时，即认为目标可被毁伤。

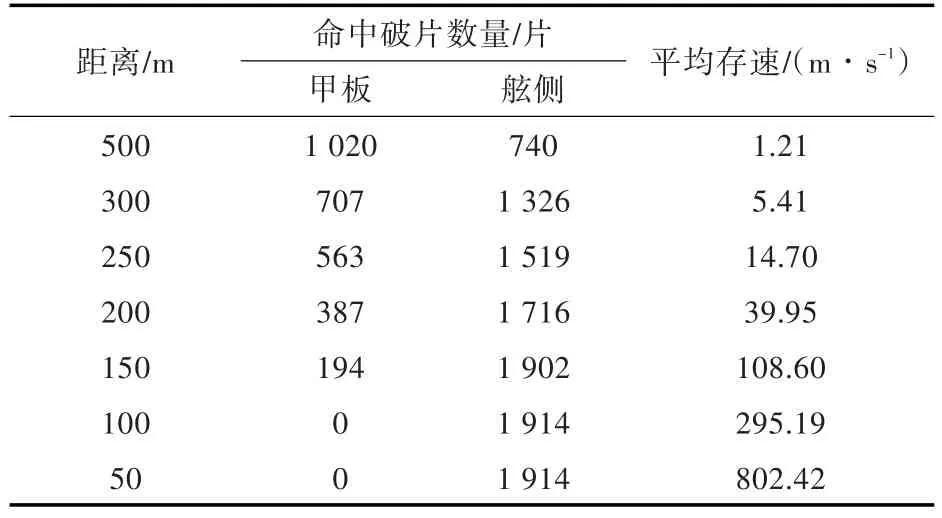
表3 破片命中舰艇的数量及平均存速Table 3 The number of fragments and the average speed hitting the ship

表4 爆炸冲击波超压对舰艇各部分的毁伤判据及毁伤威胁距离Table 4 Damage criteria and damage threats of different parts ofwarship byexplosiveshock wave overpressure

由表4可知，当炸点距离小于或等于19 m时，空气爆炸冲击波能毁伤舰员；当炸点距离小于或等于11 m时，爆炸冲击波能毁伤舰载机；当炸点距离小于或等于9 m时，爆炸冲击波能毁伤无装甲防护装备；当炸点距离小于或等于8 m时，爆炸冲击波能毁伤有装甲防护装备。

4.2 破片毁伤效应

甲板和舷侧的钢板材料为舰船专用钢，舰载机和无装甲防护设备的等效模型为6 mm厚的Q235钢板，有装甲防护设备的等效模型为12 mm厚的Q235钢板。为简化计算，根据强度极限相似原则，将舰载机及舰面技术装备均等效为一定厚度的舰船专用钢板。舰艇各目标的等效靶板厚度如表5所示。

破片毁伤元对舰艇甲板、舷侧、舰载机及其他舰面设备的毁伤程度取决于命中目标的杀伤破片数量。杀伤破片是指最大穿透厚度不小于等效靶板厚度的破片，因此破片对目标形成穿孔的动能应不小于目标动态变形功，即［11］

表5 舰艇各目标的等效靶板厚度Table 5 Average target plate thickness for each target of the ship

式中：Ef为破片动能；K1为比例系数，其值取决于目标材料的性质和打击速度；为破片与目标相遇时的面积；b为目标材料厚度。

将相关参数代入式（24），即可获得破片对舰船专用钢板的最大穿透厚度δ的计算经验公式［11］：

式中：δ为最大穿透厚度，mm。

破片对舰员的毁伤程度同样取决于命中舰员目标的杀伤破片数量。对于舰员而言，可以依据动能标准来定义杀伤破片，着靶时动能达到78.4 J的破片即为杀伤破片［6］。

将表5所示的舰艇各目标等效靶板厚度代入式（25），即可得到能够毁伤各目标的杀伤破片最小质量me。将mf=me代入式（22）和式（23），就可以计算出在不同炸点距离命中舰艇各目标的杀伤破片数量的数学期望。

1）破片对舰艇结构的毁伤。

由表3可知，当炸点距离舰艇150～500 m时，战斗部爆炸产生的前向破片能够命中甲板，但由于破片质量小于杀伤破片的最小质量，所以不会对甲板造成任何毁伤；当炸点距离舰艇小于或等于100 m时，破片不能命中甲板。因此，在炸点距离舰艇50～500 m范围内，破片毁伤元不会对甲板造成毁伤。

在炸点距离舰艇100～500 m范围内，由于命中舷侧的破片质量达不到杀伤破片的最小质量，因此杀伤破片数量为0，即没有破片能穿透12～22 mm厚的舷侧钢板；当炸点距离舰艇50 m时，能穿透厚度为12 mm舷侧钢板的杀伤破片数量的数学期望是3，能穿透厚度为15 mm舷侧钢板的杀伤破片数量的数学期望是1，能穿透厚度为18 mm以上舷侧钢板的杀伤破片数量的数学期望是0。

2）破片对舰面人员和装备的毁伤。

随着炸点距离不同，杀伤破片命中舰面人员和装备的情况如表6所示。在炸点距离舰艇50～500 m范围内，破片不会对舰载机和舰面装备造成毁伤；在炸点距离舰艇300～500 m范围内，破片不会毁伤人员；当炸点距离小于或等于250 m时，破片将毁伤舰员。

表6 命中舰面人员和装备的杀伤破片数量的数学期望Table 6 The number of effective fragments hitting the crew and equipment of the mathematical expectations

5 结 论

针对“捕鲸叉”反舰导弹和大型水面舰艇的典型结构模型，本文通过建模与计算，得到如下结论：

1）在50～500 m炸点距离范围内，爆炸冲击波不会对舰艇结构、舰面固定翼飞机、舰面设备和舰员造成毁伤。

2）在50～500 m炸点距离范围内，破片不会对甲板造成毁伤，对舷侧的毁伤威胁距离在50～100 m之间。

3）在50～500 m炸点距离范围内，破片不会对舰面固定翼飞机和舰面设备造成毁伤，对舰员的毁伤威胁距离在250～300 m之间。

本文所建立的模型和计算方法可以用于反舰导弹近距空爆的毁伤威胁性定量分析，并为相关研究提供依据和技术支撑。

［1］郑红伟，陈长海，侯海量，等.破片尺寸对空爆冲击波及破片传播过程的影响仿真分析［J］.中国舰船研究，2017，12（6）：73-80.ZHENG H W，CHEN C H，HOU H L，et al.Simulation analysis of effects of single fragment size on air-blast wave and fragment propagation［J］.Chinese Journal of Ship Research，2017，12（6）：73-80.

［2］张庆明，周兰庭.一种典型的反辐射导弹战斗部评价［J］.北京理工大学学报，1993，13（4）：511-518.ZHANG Q M，ZHOU L T.Assessment of typical anti-radar missile warhead［J］.Journal of Beijing Institute of Technology，1993，13（4）：511-518（in Chinese）.

［3］汪德武，李卫平.杀爆战斗部破片对地面目标杀伤概率的工程算法［J］. 含能材料，2007，15（3）：265-268.WANG D W，LI W P.Engineering calculation method for the lethal probability of blast-fragmentation warhead ［J］.Chinese Journal of Energetic Materials，2007，15（3）：265-268（in Chinese）.

［4］许勇，方洋旺，伍友利，等.反辐射导弹攻击航母毁伤效能分析［J］.火力与指挥控制，2009，34（11）：19-21，25.XU Y，FANG Y W，WU Y L，et al.The damage effectiveness analysis of anti-radiation missile for attacking aircraft carrier［J］.Fire Control&Command Control，2009，34（11）：19-21，25（in Chinese）.

［5］侯学隆，罗木生.捕鲸叉反舰导弹新发展与技术性能［J］.飞航导弹，2017（1）：21-28.HOU X L，LUO M S.New development and technical performance of Harpoon anti-ship missile［J］.Winged Missiles Journal，2017（1）：21-28（in Chinese）.

［6］隋树元，王树山.终点效应学［M］.北京：国防工业出版社，2000.SUI S Y，WANG S S.Terminal effects［M］.Beijing：National Defense Industry Press，2000（in Chinese）.

［7］MOTT N F.Fragmentation of shell cases［J］.Proceedings of the Royal Society of London， 1947， 189（1018）：300-308.

［8］WEIBULL W.A statistical distribution function of wide applicability［J］.Journal of Applied Mechanics，1951，13（2）：293-297.

［9］徐豫新.破片杀伤式地空导弹战斗部杀伤概率计算［D］.太原：中北大学，2008.XU Y X.The simulation of damage probability on the fragment air-defence warhead［D］.Taiyuan：North University of China，2008（in Chinese）.

［10］黄俊卿，马亚龙，范锐，等.基于数值仿真的破甲弹毁伤某型装甲装备研究［J］.系统仿真学报，2014，26（10）：2311-2314.HUANG J Q，MA Y L，FAN R，et al.Numerical simulation research of HEAT warhead mar armor target［J］.Journal of System Simulation，2014，26（10）：2311-2314（in Chinese）.

［11］王凤英，刘天生.毁伤理论与技术［M］.北京：北京理工大学出版社，2009.