基于典型舰船结构特征的陆地靶标设计方案
吴子奇,徐振桓,王志凯,王治,姚熊亮
哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001
0 引 言
水面舰船通常受到来自顶空攻击和掠海飞行反舰导弹的威胁[1]。以往,是以侵彻钢质均厚板架的厚度来标定反舰导弹的侵彻打击能力[2],然而,实际的舰船结构均为布置有纵桁和横梁的正交薄板板架结构[3],并无目标厚度均厚的钢板结构,因此,目标厚度均厚钢板结构靶板无法完全反应出舰船结构的实际毁伤特征以及导弹在多层板架间弹道偏转和飞行的姿态特征[4]。
本文拟以典型设计参数和工况的反舰导弹为输入条件,基于典型水面舰船板架结构形式及材料机械力学性能[5],依据弹道与空间各层靶板弹着点的位置关系,并适当考虑靶标固定端的边界条件以及材料的影响[6],初步设计符合舰船结构特征的多层陆地靶标,考虑试验场地等客观限制条件,提出可用于考核反舰导弹对典型水面舰船实际侵彻打击能力的多层舰船陆地靶标系统[7]设计方法。
1 舰船实际板架与等效均厚板架特性分析
1.1 反舰导弹输入条件及侵彻能力分析
典型的弹—靶侵彻模型如图1所示。其中,导弹速度v方向与板架法线的夹角α为导弹着角,主要影响导弹弹道;而导弹轴线与速度方向的夹角β为导弹攻角,主要影响导弹自身翻转。本文选取典型反舰导弹重量为200 kg,长径比为6,可侵彻穿透50 mm均厚钢板,攻角3°,着角40°,以750 m/s的速度斜侵彻的典型工况为输入条件进行研究。
通过LS-DYNA有限元软件,采用拉格朗日算法,对上述弹—靶侵彻模型进行数值计算。如图2所示,板架尺寸为8 m×8 m,选取刚性固定边界条件,板架采用船用高强度钢,其中材料密度ρ=7 850 kg/m3,弹性模量E=2.1×1011N/m2,泊松比μ=0.3,硬化模量Et=1.448×109N/m2,屈服应力σst=440 MPa。依据以往文献资料,侵彻板架时,导弹自身不发生明显的变形及损失,因此将导弹材料进行理想化处理,设置为无限强。为了提高计算精度并尽量节约计算资源,将板架被弹体侵彻区域的网格进行细化,其他区域网格尺寸保持恒定。
图3为导弹侵彻过程示意图。由图可知,该厚度板架除侵彻破口区域以外,板架塑性区域面积较小。
在上述工况下,导弹侵彻50 mm均厚钢板,其速度、着角和攻角变化如图4和图5所示。导弹剩余速度约为728.6 m/s,且攻角和着角几乎无变化,后续研究将以该剩余速度作为导弹侵彻能力的判定条件。
1.2 舰船实际板架与等效均厚板架毁伤模式分析
以导弹攻角为理想弹道,根据弹道几何特征及板架毁伤范围,初步确定各层板架尺寸(4.5 m×4.5 m)及其位置关系。由船舶结构力学可知,板架在强力构件处的边界条件可近似为刚性固定边界,所以板架四周设置为刚性固定[8]。舰船板架为布置有横向和纵向T型材及球扁钢等加强筋结构的正交各向异性板,依据质量等效原则,将舰船实际板架结构转化为等效均厚板,并和实际板架侵彻毁伤模式进行对比。板架材料和导弹参数与典型的弹—靶侵彻模型一致,每层板架的间距为2.5 m,具体参数如表1所示。
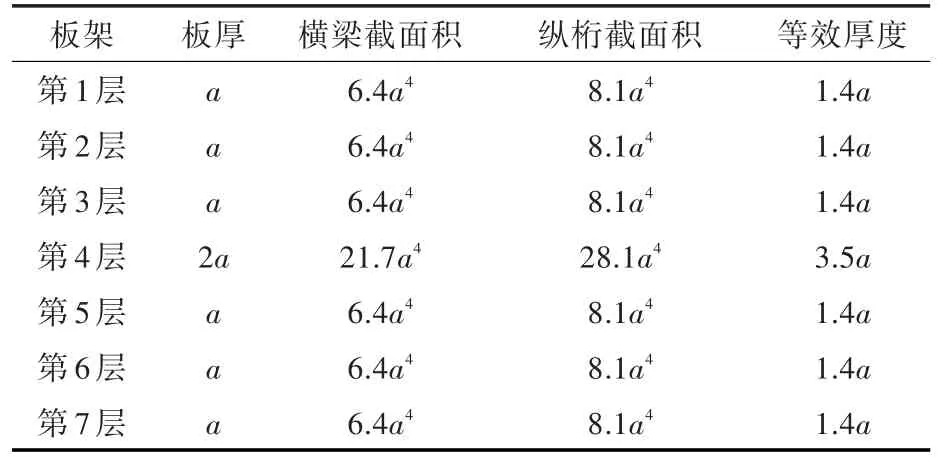
表1 实际板架结构与等效厚度板架参数Table 1 The parameters of actual panel structure and equivalent thickness plate
导弹侵彻全部板架的情况如图6所示。
导弹侵彻多层舰船板架的速度变化如图7所示。在侵彻过程中,导弹速度呈阶梯式下降,各层平台速度即为穿透板架后在抵达下一层板架前的飞行速度。导弹侵彻舰船等效均厚板架时,其速度损失相近,速度呈线性下降规律。导弹侵彻舰船实际板架时,前3层舰船实际板架的速度损失量相近,而侵彻第4层实际板架的速度损失量明显大于其他板架。以50 mm均厚钢板侵彻剩余速度为判定条件,导弹可侵彻穿透7层等效均厚板架,但仅可侵彻穿透4层实际板架,因此,单独以导弹剩余速度作为导弹侵彻能力的判据不够充分。
导弹侵彻多层舰船板架的着角与攻角变化如图8所示。由图可见,导弹侵彻舰船实际板架的着角略大于侵彻等效均厚板架的着角,由此导致一定程度的弹道偏移。如图9所示,导弹侵彻舰船实际板架和等效均厚板架时,较理想弹道均产生一定的偏移;而与侵彻实际板架产生的弹道偏移相比,侵彻等效均厚板架产生的弹道偏移几乎可以忽略,由此说明板架加强筋结构对导弹弹道有一定的影响。
随着导弹侵彻过程的不断深入,攻角不断增大,即导弹自身发生翻转。研究表明,当导弹自身与板架的法向夹角大于60°时,可能会发生跳弹现象,或者导弹自身发生折断[9]。当侵彻至对应板架时,导弹侵彻舰船实际板架的攻角明显大于侵彻等效均厚板架的攻角,即板架加强筋结构加剧了导弹自身的旋转程度。以极限侵彻角度作为判定条件,导弹可侵彻穿透6层等效均厚板架,而对于实际板架,仅可侵彻穿透4层。
经综合比较,板架加强筋结构对导弹侵彻后剩余速度和侵彻角度有显著影响,在研究导弹侵彻的过程中,不能将舰船加筋板结构等效为均质板架。因此,用于考核反舰导弹侵彻打击能力的靶标需要设计为多层结构,并且每层靶板均为正交异性薄板结构。
2 基于舰船结构特征的陆地靶标设计
由于弹靶系统的复杂性,在设计靶标的过程中,需要对其结构进行模型化处理,以使靶标模型的材料属性、结构形式、动力学性能与舰船实际相近,同时还要具备可加工性、安装性以及经济性,因此提出如下假设。假设各层靶板侵彻破口附近的塑性变形区域在弹径的3倍以内,据此确定各层靶板的最小尺寸特征[10]。当导弹质量远远小于靶标质量时,可以忽略侵彻过程中靶标的整体运动。由于材料的温度不敏感性及侵彻过程的瞬时性,忽略靶标系统的一切热效应[11]。
2.1 舰船靶标系统设计方案
基于第1节的研究,初步确定各层靶板层数、尺寸及破坏形式。依据典型的输入条件和工况,确定弹道与弹着点位置关系,由此确定靶标系统的结构形式。设计方案与舰船结构特征对应,即各层靶板均为布置横梁、纵桁(纵骨)的正交异性板,且板与板之间不相互独立,而是由型材围合而成,由此设计的舰船靶标应该为一个完整、统一且形成闭环的系统。选取水面舰船的船中位置,考核最严酷条件,即使弹着点落在各层靶板中心纵骨与横梁交会处附近,适当调整各层靶板高度,靶板上布置有不同型号的T型材。具体参数如表2所示,每层靶板的大小为3.5 m×3.5 m,靶板材料采用上述特种钢,靶板间距为2.5 m。

表2 靶标系统各层板架参数Table 2 The frame parameters of target system
各层靶板均固定在框架结构上,各层框架结构顶端与底端采用T型材构件连接,两侧采用与框架垂直的扁钢连接,扁钢通过与框架平行的纵骨固定,以确保扁钢结构的稳定性。通过这种连结形式,使靶标的每一部分形成一个整体,从而与实际舰船结构更接近。根据船舶结构力学,板架在强力构件处的边界条件可以近似等效为固定边界条件。将靶标系统与地面固定,后端支架对靶标系统固定,形成一个强框架系统,以此模拟各层靶板边界条件。整个靶标系统如图10所示。
2.2 舰船靶标系统数值预报
以上述典型工况为输入条件,基于典型舰船结构特征的靶标系统侵彻毁伤模式如图11所示。由图可知,导弹穿透了4层。
计算得到导弹侵彻各层靶板的速度、角度及弹道偏移如表3所示。

表3 导弹侵彻各层靶板的速度、角度及弹道偏移Table 3 Velocity,angle and trajectory deviation for missile penetration through target plates
设计之初,由于导弹自身的偏转,弹道会发生偏移。通过调整每层靶板在垂直方向上的高度,使得战斗部均打击在靶板的中心处、着弹点位于强横梁处,特别是第1,3,4层这3块靶板的着弹点位于横梁和纵桁交会处。通过数值预报,靶标毁伤模式以及导弹运动规律与实际情况相近(图12)。
各层靶板破口尺寸随侵彻角度的增大呈现增大的趋势。第1层靶板破口位于靶板中心横梁与纵桁交会处,由于侵彻第1层靶板时战斗部速度最快,侵彻角最小,所以破口较小,对横梁和纵桁的撕裂较小;随着侵彻角度的增大以及导弹自身的翻转,第2层靶板的破口明显大于第1层,并且加强筋有明显的撕裂现象;第3层和第4层靶板破口位于靶板中心横梁与纵桁交会处,破口附近有碟形弯曲塑性变形,同时伴随有加强筋拉伸断裂破坏现象。受导弹输入条件及板架结构的限制,破口形状呈葫芦型。各层靶板破口尺寸对比结果如图13所示。
3 结 论
本文通过导弹侵彻舰船板架结构的数值仿真,得出导弹侵彻正交加筋板与等效均厚板的差异,基于仿真结果初步设计了符合舰船实际结构特征的陆地靶标系统,并对陆地靶标系统进行数值预报,得出如下结论:
1)板架加强筋结构严重影响导弹侵彻的剩余速度、弹道特性以及导弹姿态。
2)多层等效均厚薄靶均不足以反应导弹实际侵彻打击能力以及对舰船结构的实际毁伤效果。
3)本文靶标设计方案中,靶标毁伤模式以及导弹运动规律与实际情况相近,因此陆地靶标可用于评估舰船结构毁伤模式和导弹运动规律,从而反映导弹对水面舰船的实际打击能力以及毁伤效果。
[1]隋先辉,毕开波,孙松涛,等.舰舰导弹战斗部现状与发展[J].制导与引信,2013,34(2):44-48.SUI X H,BI K B,SUN S T,et al.Present situation and development of ship to ship missile warhead[J].Guidance&Fuze,2013,34(2):44-48(in Chinese).
[2]周岩,唐平,常敬臻,等.舰舷结构与均质靶板等效关系的基本方法[J].弹道学报,2008,20(1):30-34.ZHOU Y,TANG P,CHANG J Z,et al.Basic method for equivalent relation between structure of warship and homogeneous target[J].Journal of Ballistics,2008,20(1):30-34(in Chinese).
[3]张宁.均质靶板和加筋靶板抗弹性能的数值模拟研究[J].兵器装备工程学报,2016,37(2):30-33.ZHANG N.Numerical simulation for effect of homogeneous and stiffened plates on resisting projectile penetration[J].Journal of Ordnance Equipment Engineering,2016,37(2):30-33(in Chinese).
[4]李建平,程军,熊伟,等.穿甲弹对均质装甲板毁伤效能的数学研究[J].弹箭与制导学报,2015(2):76-78,92.LI J P,CHENG J,XIONG W,et al.Mathematical research of the penetrators damage effectiveness on the homogeneous armor plate[J].Journal of Projectiles,Rockets,Missiles and Guidance,2015(2):76-78,92(in Chinese).
[5]张阿漫,杨树涛,姚熊亮.高速弹丸侵彻储油容器液固耦合数值分析[J]. 船舶力学,2010,14(9):998-1007.ZHANG A M,YANG S T,YAO X L.Numerical simulation of the penetration of fuel-filled tank by a high-speed projectile[J].Journal of Ship Mechanics,2010,14(9):998-1007(in Chinese).
[6]施惠生.材料概论[M].上海:同济大学出版社,2003.
[7]王建刚.子弹侵彻钢筋混凝土的数值模拟研究[D].北京:国防科学技术大学,2001.
[8]陈铁云,陈伯真.船舶结构力学[M].上海:上海交通大学出版社,1991.
[9]朱光辉.动能弹斜侵彻混凝土靶跳弹规律分析[D].南京:南京理工大学,2007.
[10]王政.弹靶侵彻动态响应的理论与数值分析[D].上海:复旦大学,2005.
[11]赵国志.穿甲工程力学[M].北京:兵器工业出版社,1992.

