基于物质点法的弹体侵彻靶板破甲特性数值模拟

秦业志，姚熊亮，王志凯，王莹

哈尔滨工程大学 船舶工程学院，黑龙江哈尔滨150001

0 引 言

现代海战中，舰船结构在遭受鱼雷、反舰导弹等接触攻击时，在弹体的穿甲作用下易造成板壳结构的毁伤。舰船壳板穿甲过程是一个非线性、高瞬态的过程，它涉及到了材料大变形表现出的物理非线性、结构接触、材料摩擦等问题，因此具有一定的复杂性［1］。舰船板壳结构穿甲研究的方法通常采用理论研究、实验和数值模拟等方法。随着计算机技术的飞速发展，计算成本日益降低，数值算法日臻成熟，使数值模拟成为研究穿甲问题时采用的主要方法。

目前，数值模拟船壳板结构穿甲过程的主要方法为有限元法和无网格法。基于拉格朗日描述的有限元方法是将网格附着在材料上，随着材料的变形，网格也随之变形，其基本思想是将函数定义在简单的几何形状的单元域上，通过插值函数计算单元场内函数的近似解，从而得到整个求解域内的近似解。对于用有限元法处理弹体高速侵彻靶板的问题，材料发生大变形，单元容易产生严重的畸变，造成计算精度下降，甚至是导致计算中止。可见，对于极端大变形的问题，有限元法存在缺陷，特别是在模拟弹体侵彻靶板的过程中不能很好地模拟靶板破口的形态及动态形成过程。而无网格法在处理大变形问题时则体现出了优势。

最初，人们普遍认为无网格方法是上世纪70年代提出的光滑粒子流体动力学（Smoothed Particle Hydrodynamic，SPH）方法。SPH方法当时主要用于研究天体物理学问题，经过几十年的发展，已被广泛应用于爆炸与冲击动力学、水动力学、流体碰撞雾化等领域，且取得了显著的研究成果［2］。此后，无网格法的研究得到了国内外学者的广泛关注，提出了许多新的无网格法。典型的无网格法包括多种方法，如伽辽金型无网格法、配点型无网格法、基于局部弱形式和边界积分方程的无网格法、最小二乘法和物质点法（Material Point Method，MPM）［3-4］。1994年，Sulsky等［5-6］将质点网格（Particle-in-cell）方法应用到了固体力学问题的研究中，并对数值方法进行了改进，由此提出MPM法。如今，该方法已成功应用于材料破坏、碰撞冲击、生物力学等问题的研究，尤其是在处理材料破坏及材料大变形的问题时具有很大的优势。MPM法是一种质点类无网格方法，它将连续体离散成一组携带有所有物质信息的物质点，通过物质点的运动表示物体的变形。同时，将物质点固联到背景网格上，背景网格可以固定或自由布置，从而用于动量方程的求解和空间导数的计算。在求解过程中，物质点和网格点没有相对运动，避免了欧拉法因非线性对流项产生的数值困难，并且极易跟踪到物质界面。而在下一时间步中，仍采用未变形的背景网格，抛弃变形后的背景网格，因此避免了拉格朗日法因网格畸变而产生的数值困难。MPM法发挥了拉格朗日方法和欧拉方法各自的优点，非常适合用于分析超高速碰撞、侵彻等问题。例如，Lian等［7］运用MPM法成功模拟了钨弹侵彻钢靶等问题。Ma等［8］基于局部多重背景网格的物质点算法模拟了中、低速侵彻问题。马上等［9］运用MPM法研究了弹丸高速碰撞板的一系列问题。

本文针对弹体侵彻船用钢板的破甲特性，将重点研究靶板破坏形成的动态过程以及靶板的破坏形式，采用MPM法研究得到与实验结果吻合较好的数值仿真结果，以验证MPM法的有效性，从而为研究弹体侵彻船用钢板材料的破甲问题提供新的研究途径。

1 物质点算法

1.1 控制方程及物质点离散

本文不考虑热效应，更新拉格朗日格式的控制方程如下［10-11］。

质量守恒方程：

式中：为现时构形物体的密度；为雅克比行列式；为物体初始时刻的密度。

动量守恒方程：

式中：σij为柯西应力张量，其中i，j为空间坐标的分量；ρ为当前时刻的密度；bi为作用在物体单位质量上的体力；为在i方向的加速度。

能量守恒方程：

式中：̇为单位质量的内能；Dij为变形率张量。

本构关系：

式中：σ∇为焦曼应力率。

几何方程：

式中：为应变率；vi，j和vj，i为质点在空间坐标i，j方向的速度分量。

边界条件：

式中:nj为材料边界的单位法线方向；Γt和Γv分别为现时构形中指定的面力边界和速度边界为质点在i方向的速度；分别为指定的面力和速度。

初始条件：

式中为质点在i方向的位移；为质点在i方向的速度为质点在i方向的初始位移；为质点在i方向的初始速度。

MPM法将连续体离散成一组质点，如图1所示。图中，V为材料体积域，Vp为质点的体积域，Γ为构形中的指定边界。每个质点代表一块材料区域，同时携带物质信息，包括质量、速度、应力和应变等。物质点固连在背景网格内，背景网格用于计算空间导数及求解物体运动。

因此，离散连续体的密度ρ(xi)可以近似表示为

式中：np为质点总数；mp为质点p的质量；δ为Dirac Delta函数；xi为质量的坐标；xip为质点p的坐标。

在求解动量方程时，物质点和背景网格完全固连，并随网格一起运动，因此，可建立背景网格结点上的有限元形函数NI(xi)来实现物质点和背景网格结点坐标之间信息的映射关系，如式（9）所示［12］。其中，带下标I，J的量表示该网格结点变量，带下标p的量表示质点携带的变量物质点和该网格结点坐标之间的映射关系，即

式中：为网络结点I的形函数在质点处的值；uiI为结点I在i方向上的位移。

背景网格结点的运动方程为

背景网格结点I的内力为

式中：σijp为质点的柯西应力张量。

背景网格结点I的外力为

式中，h0为假想边界层的厚度。

1.2 MPM求解方法

MPM法的求解有不同的实现格式，Sulsky和Bardenhagen等［5，13］讨论了 2 种更新的应力求解格式 ，即 USF（Update Stress First）和 USL（Update Stress Last）格式。质点上的应变率是基于更新后的网格结点速度得到。此外，有人提出了一种改进的USL格式，即MUSL（Modified Update Stress Last）格式，并得到了广泛应用，如下式［14］。

式中：NpI，i和NpI，j分别为网格节点I的形函数在质点处i，j方向的值；vIi，vIj分别为网格结点I在i，j方向的速度。上标n，n+1/2分别表示tn，tn+1/2时刻。

根据网格结点速度计算方法的不同，得到不同的求解格式如下：

1）USF格式。首先在每个时间步计算应变率，然后更新应变率，利用更新前的结点动量计算结点速度，最后代入式（15）得到应变率

2）USL格式。直接用网格结点动量来计算结点速度，即

式中，为网格结点I在i方向n时刻的动量。

3）MUSL格式。将更新后的网格结点动量映射到背景网格后再次计算结点的速度，

式中，vp i为质点在i方向的速度.

在本文研究中，采用MUSL格式的求解方法。

1.3 材料本构模型及物态方程

弹体和靶板的材料分别为D6A钢和船用外壳921钢，它们均采用Johnson-Cook本构模型，而状态方程则采用Mie-Grunesien状态方程。D6A钢的层裂强度取为7.68 GPa，921钢的层裂强度取为 6.24 GPa［15］。

Johnson-Cook本构模型屈服应力表达式为

式中：σ0为静态屈服强度；B0和n为应变硬化参数；C为应变强化参数；m为热软化参数；εe为等效塑性应变；为等效塑性应变率；为参考应变率；T*为无量纲温度，且，其中Tm为熔点温度，Tr为室温，e为内能，e0为高能炸药单位质量的内能，CV为比热。

Mie-Grunesien状态方程表达式为

式中：γ为Gruneisen常数；PH为冲击Hugoniot曲线上点的压力；ξ为爆轰产物中的相对比容。

此刻，盗走尸体的这只山精，体型粗壮，比成人还要高着一头，一身漆黑油亮的毛，蓬松而茂密，一看便是一只正处壮年的雄性山精。

弹体和靶板的具体参数［16］如表1所示。

表1 材料模型参数Table 1 The parameters of material model

2 物质点法验证

本文研究的弹体采用实心球头，直径为25 mm，球头半径为12.5 mm，弹体靶前速度V0=280 m/s，如图2所示。弹体所用材料为硬度很高的D6A特种钢，通常用于弹体的制造。靶板尺寸为400 mm×400 mm×5 mm，材料为应变率敏感的921钢。

模拟中，弹体以V0=280 m/s的速度冲击靶板，随后靶板产生塑性大变形，弹体速度随着时间的增加而减小，穿过靶板后，弹体以稳定的速度向前运动，并最终衰减为靶后速度V1=185 m/s，其与实验结果相差不大。图3所示为弹体侵彻靶板各时刻的破坏情况。图4所示为弹体穿透靶板后的变形状态。图5所示为靶板背面的破口变形状态。

由图3～图5可以看出，弹体以V0=280 m/s的速度冲击靶板，靶板产生冲塞破坏，且随着时间的增加，靶板产生的塑性变形增大，靶板材料受到严重的挤压，产生大的变形，形成盘形凹陷。随着弹体的继续运动，靶板材料在运动方向上持续变形，当靶板材料隆起的塑性变形达到一定程度后，断裂形成的冲塞体从靶体中飞离，沿着穿透方向继续向前运动。当弹体穿透靶板后，靶板面上形成一个近似圆形的靶孔，其直径与弹体直径相近。表2所示为采用MPM法和实验方法得到的弹体冲击靶板过程中的结果，由表2可知两种结果比较接近，相对误差小于6%。

表2 弹体侵彻靶板的MPM法和实验结果比较Table 2 Comparison of results acquired by MPM and experiment when the projectile penetrating target plate

3 弹体侵彻靶板数值模拟结果分析

本文基于建立的数值仿真模型，研究了弹体以不同靶前速度分别侵彻5和10 mm厚靶板时的破甲特性，并运用MPM法对弹体侵彻靶板的过程进行了仿真。弹体侵彻后靶板的破坏形态如图6和图7所示。

对于研究弹体侵彻靶板的问题，重点关注了靶板破口直径和弹体剩余速度（即靶后速度）。由图8、图9以及表3可知：当弹体从中、高速和超高速状态冲击靶板时，靶板破口在26～35 mm之间；对于5 mm厚靶板的破坏形态，弹体速度越高，靶板破口直径越小；在高速、超高速冲击状态下，靶板破口几乎与弹体直径相同，随着弹体初速的增加，靶板冲塞破口隆起的高度也随之增大，但弹体自身几乎未发生变形；当靶板厚度为10 mm时，靶板破口直径同样略大于弹体直径，随着弹体速度的增加，靶板隆起高度的规律与薄板一样，即隆起高度减小，但其明显的区别是弹体头部出现了变形。当撞击厚板时，弹体头部形状发生变形，而侵彻靶板时弹体几乎不发生变形。在同样的侵彻速度下，侵彻厚板比侵彻薄板产生的破口隆起的高度要小，厚板的破口半径略小于薄板，侵彻厚板的弹体变形比侵彻薄板的变形要大。对于弹体侵彻靶板，靶板越厚，弹体减小的速度幅度越大，消耗的能量就越多，故板厚影响了弹体最终的剩余速度，这一结论对于研究弹体侵彻多层靶板具有参考意义［17］。

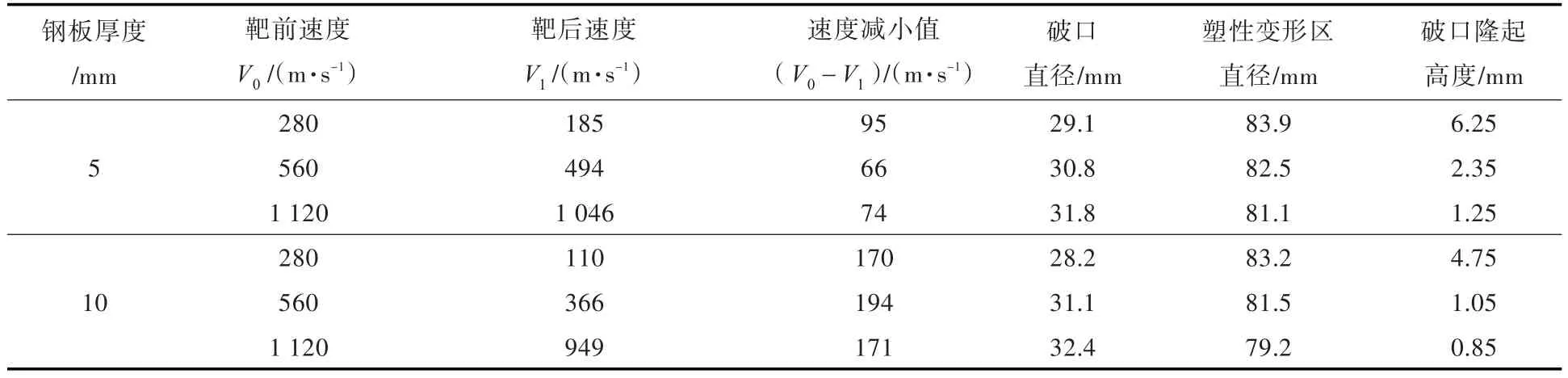
表3 弹体侵彻靶板的仿真结果比较Table3 Simulaiton results comparison of the projectile penetrating target plate

4 结 论

本文根据MPM法在模拟超高速碰撞方面的优势，特别是能够较好地模拟靶板破口的形成过程，建立了导弹侵彻舰船典型的板壳结构数值模型，仿真结果验证了MPM法的有效性。在此基础上，用该数值方法研究了弹体速度变化和靶板板厚变化下的破坏形态，得出如下结论：

1）MPM法数值模拟结果与实验结果吻合较好，说明采用MPM法模拟船体板壳穿甲问题完全可行。对于舰船板壳结构受到弹体冲击的大变形问题，MPM法不仅可以模拟靶板材料的破坏形式，还可以对材料的破坏程度进行评估，故是一种研究舰船板壳结构穿甲问题的新的有效方法。

2）以25 mm直径弹体为例，模拟其以不同速度侵彻5和10 mm厚靶板，得到靶板破口直径在26～29.5 mm之间，塑性变形区的范围大小几乎不变，约30 mm；弹体速度对靶板破口的影响很小，但对靶板冲塞破口隆起的高度影响较大；弹体速度越高，靶板越厚，弹体头部更会产生变形。弹体侵彻靶板的破坏属于冲塞穿甲形式，符合实验研究的规律。

3）本文建立的数值模型能够很好地模拟弹体侵彻靶板的破坏形成过程，相对误差小于6%，模拟精确度高，所以本方法具有可行性，数值模拟结果可用于指导实验设计，并为舰船横舱壁防护设计提供参考。

［1］宁建国，王成，马天宝.爆炸与冲击动力学［M］.北京：国防工业出版社，2010.

［2］LUCY L B.A numerical approach to the testing of the fission hypothesis［J］.Astronomical Journal，1977，82（12）：1013-1024.

［3］张雄，刘岩.无网格法［M］.北京：清华大学出版社，2004：1-10.

［4］张雄，宋康祖，陆明万.无网格法研究进展及其应用［J］.计算力学学报，2003，20（6）：730-741.ZHANG X，SONG K Z，LU M W.Research progress and application of meshless method［J］.Chinese Journal of Computational Mechanics， 2003， 20（6）：730-741（in Chinese）.

［5］SULSKY D，CHEN Z，SCHREYER H L.A particle method for history-dependent materials［J］.Computer Methodsin AppliedMechanicsandEngineering，1994，118（1/2）：179-196.

［6］SULSKY D，ZHOU S J，SCHREYER H L.Application of a particle-in-cell method to solid mechanics［J］.Computer Physics Communications，1995，87（1/2）：236-252.

［7］LIAN Y P，ZHANG X，LIU Y.Coupling of finite element method with material point method by local multi-mesh contact method［J］.Computer Methods in AppliedMechanicsandEngineering， 2011，200：3482-3494.

［8］MA Z T，ZHANG X，HUANG P.An object-oriented MPM framework for simulation of large deformation and contact of numerous grains［J］.CMES-Computer Modeling in Engineer&Science，2010，55（1）：61-87.

［9］马上，张雄，邱信明.超高速碰撞问题的三维物质点法［J］.爆炸与冲击，2006，26（3）：273-278.MA S，ZHANG X，QIU X M.Three-dimensional material point method for hypervelocity impact［J］.Explosion and Shock Waves，2006，26（3）：273-278（in Chinese）.

［10］周旭，张雄.物质点法数值仿真（软件）系统及应用［M］.北京：国防工业出版社，2015：1-9.

［11］张雄，廉艳平，刘岩，等.物质点法［M］.北京：清华大学出版社，2003：15-27.

［12］马上.冲击爆炸问题的物质点无网格法研究［D］.北京：清华大学，2009.MA S.Material point meshfree methods for impact and explosion problems［D］.Beijing：Tsinghua University，2009（in Chinese）.

［13］BARDENHAGEN S G.Energy conservation error in the material point method for solid mechanics［J］.Journal of Comutational Physics，2002，180：383-403.

［14］廉艳平，张帆，刘岩，等.物质点法的理论和应用［J］. 力学进展，2013，43（2）：237-264.LIAN Y P，ZHANG F，LIU Y，et al.Material point method and its applications［J］.Advances in Mechanics，2013，43（2）：237-264（in Chinese）.

［15］张林，张祖根，秦晓云，等.D6A、921和45钢的动态破坏与低压冲击特性［J］.高压物理学报，2003，17（4）：305-310.ZHANG L，ZHANG Z G，QIN X Y，et al.Dynamic fracture and mechanical property of D6A，921 and 45 steels under low shock pressure［J］.Chinese Journal of High Pressure Physics，2003，17（4）：305-310（in Chinese）.

［16］许庆新.基于SPH方法的冲击动力学若干问题研究［D］.上海：上海交通大学，2009.XU Q X.Study of some impact dynamics problems based on smoothed particle hydrodynamics method［D］. Shanghai： Shanghai Jiao Tong University，2009（in Chinese）.

［17］程素秋，陈高杰，赵红光.聚能战斗部对双层靶板结构毁伤的数值模拟研究［J］.中国舰船研究，2013，8（2）：53-57.CHENG S Q，CHEN G J，ZHAO H G.Numerical damage analysis of shaped charge warheads on double-deck target plates［J］.Chinese Journal of Ship Research，2013，8（2）：53-57（in Chinese）.