基于遗传算法的双目标Flow-shop调度问题研究

李文韬，陶 泽，陈晓菲

(沈阳理工大学 机械工程学院,沈阳 110159)

流水车间(Flow-shop)调度问题是车间调度问题中的一个具有代表性的经典问题，在实际问题中应用广泛[1]，具有很大的研究价值，一直是理论界和工程领域的热点问题。Flow-shop调度问题是以实际流水线车间的生产调度为依托而简化的一个模型，其工艺约束相对来说比较简单。合理的车间调度可以减少生产周期，对现有的资源进行最优分配，从而更好的完成生产任务，提高生产效率。针对一系列复杂的优化问题，遗传算法提供了通用的解决方法，基于其鲁棒性强的特点，遗传算法在医学领域、各种工业领域、甚至在服务领域都得到了应用，随着近年来的快速发展，已经成为求解全局优化问题的有力工具。

随着工业技术的迅猛发展，对车间调度问题也提出了更高的要求，对单一目标的追求已经远远不能满足实际的生产需要，需要对两个甚至多个目标进行优化。对于调度问题，Paolucci M等提出了基于仿真决策支持系统进行调度[2]；吴云高对关于两台机器的Flow-shop优化问题开展研究，建立了混合整数规划的模型，采用了分支定界算法对问题进行求解[3]。但是，由于这些方法具有周期长、解质量差等缺点往往不太适用于工程问题。相比而言，遗传算法具有并行性的特点，在搜索空间中可以同时对多个解进行评估，可以对影响目标进行综合考虑，因此，现阶段遗传算法是解决这类优化问题的重要方法和手段。本文运用遗传算法和小生境技术，对双目标Flow-shop调度问题进行探究，以生产周期和平均流时间[4]为目标模拟加工车间，通过系统仿真得出双目标Flow-shop调度问题的结果。

1 Flow-shop调度问题的描述

Flow-shop调度问题是研究流水线上工件在不同功能的机器上的加工过程，其中每个等待加工的工件都具有同样的顺序并且在每台机器上只能加工一次。因此，Flow-shop也称为同序作业调度问题。Flow-shop可以描述为：n个工件、m台机器进行流水作业加工，其加工顺序是恒定的，在一段时间内每个工件只能被一台机器加工，工件所需的各个时间均已知。Flow-shop最后需综合所有调度指标使之达到最优。

2 基于遗传算法和小生境技术相结合的调度算法

遗传算法是一种随机、并行的优化算法，是以种群开始[5]，种群则是由基因通过编码而成的染色体组成。初始化种群后，逐代产出越来越好的染色体。每代都需要通过适应度的大小进行选择，之后进行遗传算子的交叉与变异，产生新的集合即新的种群，重复以上过程直至达到某种指标可以收敛为止。但是由于遗传算法一般是优先选择更高级别染色体进行复制，往往收敛于局部最优解，降低了遗传算法的全局搜索能力，无法保证解的多样性，需要引进小生境技术，来保证解的多样性，对解决多目标调度问题具有明显的优越性[6]。将小生境技术与遗传算法相结合，对多目标优化问题进行求解，可能获得最优解。对于同级别的染色体，通过小生境技术可以选出更好的个体进行复制。改进后的的遗传算法流程图如图1所示。

图1 算法流程图

3 Flow-shop调度问题的数学模型

在建立具体的数学模型前需要对该问题做一些约束：

(1)每个零件在流水线上的加工顺序固定；

(2)每台机器在某一时刻都只能同时加工一个工件；

(3)每个工件在每台机器上都只能加工一次；

(4)工序的准备时间包含在加工时间中；

(5)每台机器的加工时间给定；

(6)每个工件不能在多台机器上同时加工。

对于一般流水车间调度问题，令c(ji,k)表示机器k加工完成零件ji的时间，tij为工件i在机器j上给定的加工时间，{j1,j2,…,jn}为工件的流水排序，则m台机器加工n个工件所用的时间是

c(j1,1)=tj11

(1)

c(j1,k)=c(j1,k-1)+tj1k

(2)

c(ji,1)=c(ji-1,1)+tji1

(3)

c(ji,k)=max{c(ji-1,k),c(ji,k-1)}+tjik其中(i=2,3,…,n;k=2,3,…,m)

(4)

本文为双目标Flow-shop调度问题，采用生产周期和平均流时间为目标约束，故目标函数为

F1=T=max(c1,c2,…,ck)

(5)

(6)

式中Fi为第i个工件的加工操作结束时间。

4 Flow-shop调度的算法实现

4.1 编码与解码

遗传算法不能直接作用于调度问题的参数，而是需要通过编码成特定结构的染色体来解决具体问题。本文根据流水车间的现实情况将工件的顺序编码成染色体，并采用十进制进行编码。例如：在流水车间里6个工件在6台机器上加工，其加工顺序为j1,j2,j5,j3,j6,j4，则可以编码为{1,2,5,3,6,4}。

4.2 适应度函数

适应度函数可以对染色体进行评价，染色体的适应度值越高遗传的概率越大，适应度值越低遗传概率就越小。而且，作为遗传算法在搜索过程中的唯一评价依据[7]，设计适应度函数的合理性显得尤为重要。如果设计不当可能会出现一些超常个体来控制遗传过程，导致早熟收敛，影响全局算法及优化性能。所以，确定合适的适应度函数是优化过程中的重中之重。

4.3 选择操作

选择操作既从当前群体中以一定的方式选出优异的个体为下一代进行繁殖。对于优先级别不同的染色体，可以根据适应度值的大小进行排列，之后按照每个适应度值大小所占的比例进行分配。假设种群的大小为A，个体i的适应值为fi，则i被选择的概率pi为

(7)

对于级别相同的染色体，运用小生境技术进行选取。通过对小生境数的计算来选取更优秀的个体进行复制，即选取小生境数相对较小的个体遗传至下一代。其计算过程如下：

(8)

(9)

(3)个体间的距离

(10)

(11)

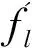
4.4 交叉操作

交叉操作是最重要的一项操作，在选择操作之后，是将父代的两个染色体的一段基因进行交叉，组成两个新的染色体，其中都包含父代的优异基因。例如：父代1：3 2 2 2 3 1 1 1 3；父代2：1 1 3 2 2 1 2 3 3；从父代1上选取一个或一段基因后，从父代2上消除对应的基因，并将该选取基因加到子代上，重复该步骤至子代染色体包含所有基因。则子代1：3 2 1 1 2 1 2 3 3；子代2：1 1 3 2 2 2 1 3 3。

4.5 变异操作

变异操作是指将原来染色体的一个基因转变成其它基因，进而生成新的染色体，可以提高局部搜索能力，保持种群的多样性，防止早熟现象的出现。变异操作按位进行，本文采用的变异方法是将染色体中原位上的基因用另一种基因进行同位置替换。

5 算例仿真

本次模拟针对双目标Flow-shop调度问题，以生产周期最小和平均流时间最短为目标，采用Delphi7.0软件进行编程并运行上述算法，是面向对象的编程技术。在工件加工时间以及加工顺序确定、同时各个工件的各项加工参数不变的情况下，使待加工工件依次进入加工系统完成加工。在本次仿真实例中，以6×6的Flow-shop调度问题为例，相关参数为：工件种类jC={j1,j2,j3,j4,j5,j6}，机器种类MC={M1,M2,M3,M4,M5,M6}，其加工时间见表1所示。

表1 工件在机器上的加工时间

仿真过程中,取仿真次数为1、2、3、4、5、6、7、8次,交叉概率为0.8,变异概率为0.01[8]。

Delphi7.0软件的仿真次数与对应结果见表2所示。

表2 仿真次数与结果

经过算法计算后，结合生产周期与平均流时间，得到遗传产生后代的双目标仿真结果。如图2所示。

图2 遗传产生的后代

在双目标的空间中，如果一个个体的横纵坐标都比其它个体的横纵坐标小，则定其级别为0；如果某个个体只有一个横坐标或纵坐标小于之前的横坐标或纵坐标，则定其级别为1，依次类推，直至所有个体的级别设置完毕。每一代中0级别为最高级别。从图2中可以清楚的看到，P2的级别显然高于其他个体，可以定其为0级，其平均流时间和生产周期时间都相对最少。因此，最终通过仿真得到的甘特图如图3所示。

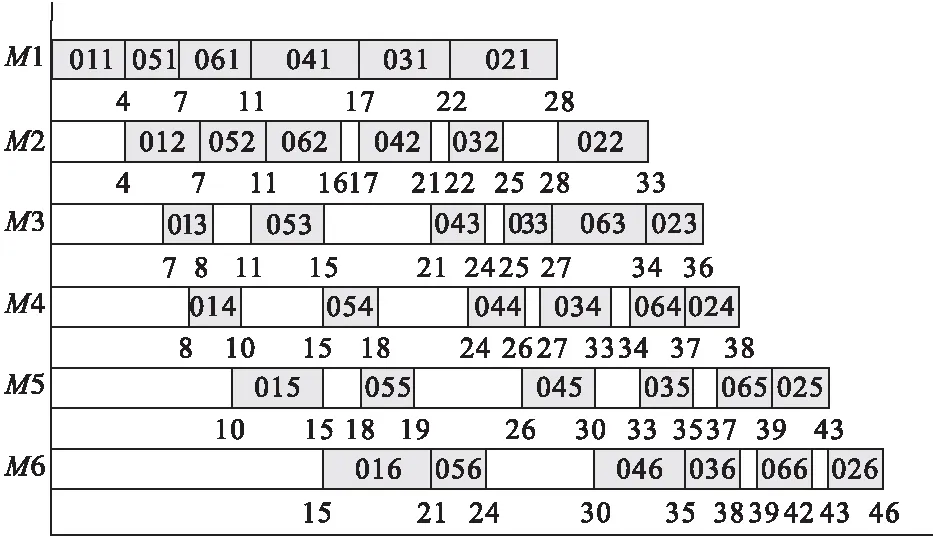
图3 双目标调度甘特图

通过甘特图可以看出，其最优的生产周期为46时间单位，同时可以清楚的反映出流水车间调度工件加工的顺序是相同的。图3与图2相结合可得出其最优平均流时间为37.3时间单位。

6 结论

分析了流水车间调度问题的特性，针对遗传算法在解决双目标Flow-shop调度问题的不足，提出了将小生境算法与遗传算法相结合的方法。此方法可以保持解的多样性并具有很高的收敛速度，既保证了生产周期最小，又保证了平均流时间最少。通过合理的参数设计建立仿真模型，最终得到的仿真结果证实该方法的可行性和有效性。

参考文献：

[1] 王凌.车间调度及其遗传算法[M].北京：清华大学出版社,2002.

[2] Paolucci M,Sacile R,Boccalatte A.Allocating Crude Oil Supply to Port and Refinery Tanks:a Simulation-based Decision Support System[J].Decision Support System,2002,22(1):39-54.

[3] 吴云高.基于遗传算法的车间调度方法及其应用[D].杭州：浙江工业大学,2002.

[4] 陈振同.基于改进遗传算法的车间调度问题研究与应用[D].大连：大连理工大学,2007.

[5] 马永杰.云文霞.遗传算法研究进展[J].计算机应用研究.2012,29(4)：150-152.

[6] 王小平.曹立明.遗传算法—理论、应用与软件实现[M].西安：西安交通大学出版社,2002.

[7] 周明,孙树栋.遗传算法原理及应用[M].第一版.北京：国防工业出版社,1998:11-24.

[8] 仁庆道尔吉.车间作业调度及其遗传算法[D].呼和浩特：内蒙古大学,2006.