连铸二冷动态控制算法研究

纪振平,田珊珊,王 纪

(1.沈阳理工大学 自动化与电气工程学院,沈阳 110159； 2.亳州职业技术学院信息工程系,安徽 亳州 236800)

对连铸机来说，二次冷却是一个非常重要的环节，传统的二冷水表控制方式在拉速突变时易使铸坯产生裂痕等问题。为避免缺陷的产生，研究者们做了大量的工作。文献[1-2]将人工神经网络或与其它算法相结合的方式应用到连铸二冷控制中，取得了良好的控制效果，铸坯的质量得到改善；文献[3-5]，基于模糊自适应控制算法对二冷水量进行调节，测试结果较好；陈伟等建立了基于子问题接近优化技术的连铸多工艺参数多约束优化系统，优化二冷配水，使铸机以高生产率、低消耗运行[6]。

设定值加权PID(Proportional-Integral-Derivative)控制器也经常被用于二冷控制。在传统的设定值加权控制算法[7]中，设定值权重是一个固定的值或三个独立的值，在稳定的系统中应用良好，但对非线性系统的响应效果欠缺。为取代固定权重，权值动态调整技术被提出[8-9]。Leva等提出基于最优化技术的平方误差积分法来得到权重因子[10]；Prashanti等提出针对一阶惯性加延迟系统，分别对控制器的比例部分和微分部分加权[11]；此外还有很多不同的优化方法被提出，皆为获得最佳的设定值权重[12-13]。

本文基于在线凝固传热模型建立不同拉速下的过程模型，并以方坯铸机为对象研究一种适用于二冷动态控制的自适应PID动态权值调整法，同时与常规PID进行仿真对比研究。

1 二冷动态控制系统组成

二冷配水动态控制即是根据各冷却段控制点的目标温度与实际温度的差值来调整冷却水量，使实际温度更快的逼近目标温度，以减少超调量和系统振荡。二冷动态控制系统结构如图1所示。

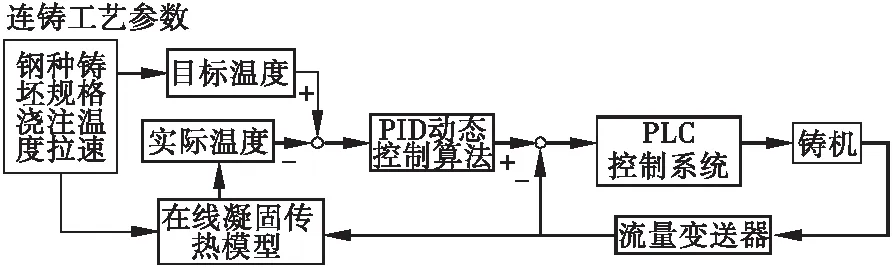
图1 二冷动态控制系统结构图

2 二冷过程模型建立

2.1 二冷水与铸坯表面温度的耦合关系

连铸冷却过程的一个显著特点是二冷区的各段冷却水量对铸坯表面温度的影响具有耦合性，并且这种耦合是单向的从上到下的耦合[14]。方坯铸机一般有多个冷却段，下面以四个冷却段的方坯铸机为研究对象，在某一固定拉速下，冷却水增量ΔQi与表面温度增量ΔTi之间的关系可以描述为

(1)

式中Gij(S)可表示成式(2)所示的传递函数的形式。

(2)

式中：i、j∈3且i≥j；τij是前段水量对后面各段耦合作用的延迟时间；Kij是过程增益；Tij是响应时间。理论上i=j时，τij=0，但在实际的二冷配水过程中，当喷嘴开始对铸坯喷水时，铸坯表面的温度不会立刻变化，通常存在2s左右的延迟。

2.2 过程模型的确定

基于在线凝固传热模型获得二冷水量变化时铸坯各段的表面温度数据，在后续的二冷水控制中已经考虑到二者的耦合关系，因此在建立二冷过程模型时仅需考虑本段水量与本段铸坯表面温度之间的关系。工程实践中通常利用两点法来确定一阶惯性数学模型，所谓两点法就是利用阶跃响应中两个点的数据去计算一阶惯性环节的参数T和τ。本文利用两点法进行数据处理后，获得拉速2.0m/min时各段的二冷过程模型，如表1所示。

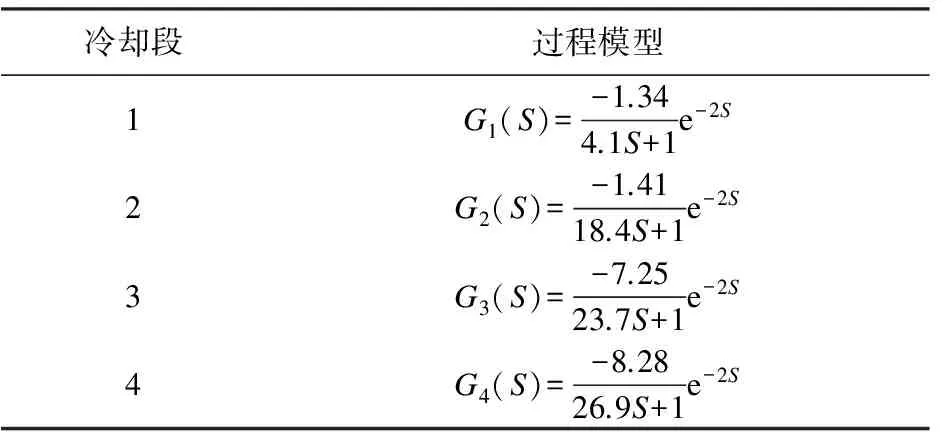
表1 拉速2.0m/min时各段的二冷过程模型

研究发现，过程模型会随着拉速的增大而增大，表2给出了不同拉速下的第四段过程模型。

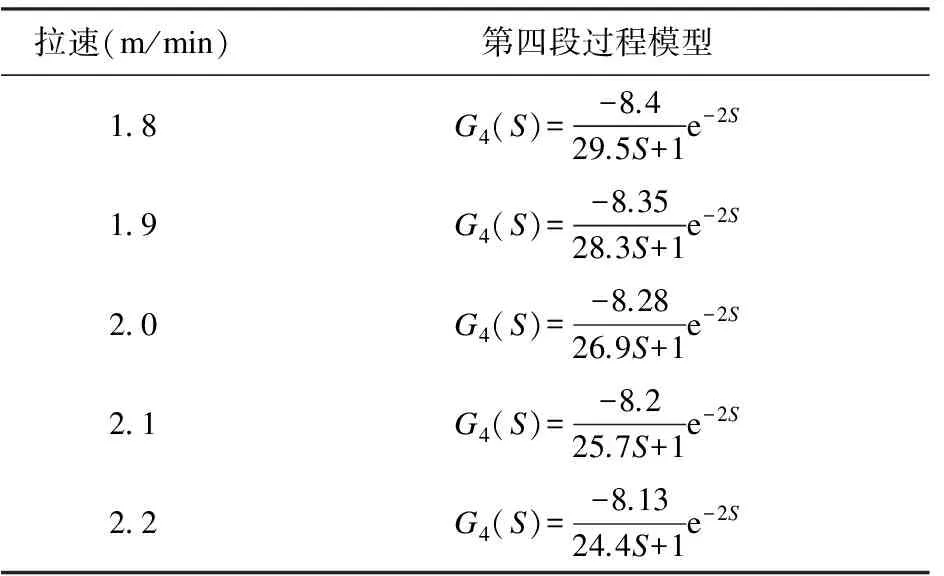
表2 不同拉速下第四段过程模型

3 PID动态权值调整法

3.1 算法描述

PID动态权值调整法[15]是一种动态调整设定值权重的PI控制算法(PI controllers through Dynamic Set-point Weighting,简称DSWPI)，通过在线自动调整设定值权重来提高PI控制器的性能，其控制原理图如图2所示。

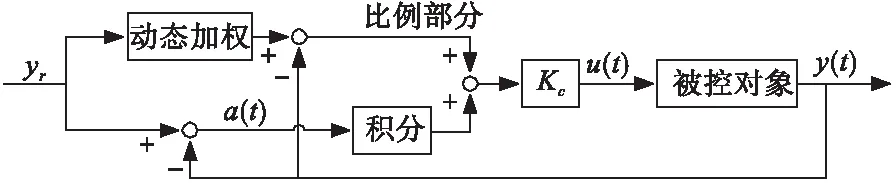
图2 动态权值调整法控制原理图

DSWPI控制器输出u(t)的离散形式为

udw(k)=kc[{βd(k)×yr-y(k)}+

(3)

式中：kc是比例增益；Ti是积分常数；yr是系统设定值；y(k)是系统输出值；a(i)是第i时刻的误差；Δt是采样周期；βd(k)是动态权重因子，βd(k)的表达式如式(4)所示。

βd(k)=1+γ×θ×Δar(k)

(4)

式中，Δar(k)是第k时刻的误差变化率；θ是过程归一化死区时间，由临界增益ku和过程增益kp定义；二者的表达式分别如式(5)和式(6)所示。

(5)

(6)

公式(4)中的γ是一个可调节参数，为适应本文提出的二冷动态控制过程，基于粒子群优化算法对γ值进行参数优化，得到当拉速为2.0m/min时不同过程模型下的γ值，如表3所示。

表3 拉速为2.0m/min时不同过程模型下的值

由公式(4)可知，动态权重因子β与系统的误差和误差的变化率有关。系统运行时，误差和误差率会不断变化，此时β值会随之自动调整，即PID控制器随着系统的变化在线实时动态调整参数，使系统快速趋于稳定。

3.2 性能分析

利用Matlab仿真平台，以表2中不同拉速下第四段水量变化时的过程模型为被控对象进行算法的控制性能分析。

3.2.1 与常规PID控制的仿真对比

以拉速为1.8m/min时的过程模型为被控对象，分别调整常规PID控制器和DSWPI控制器的控制参数，得到图3所示的系统响应曲线；保持两个控制器的控制参数不变，将被控对象改变成拉速为2.2m/min时的过程模型时，得到两种控制器的响应曲线如图4所示。

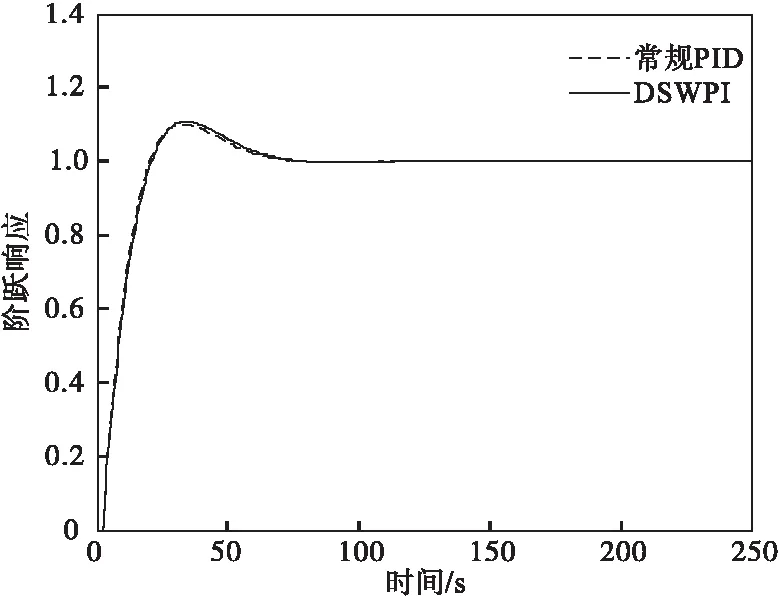
图3 拉速1.8m/min时响应曲线

由图3可以看出，两种控制器在过程模型一定时都有良好的控制效果；但当过程模型发生改变时(如图4所示)，用常规PID控制的系统出现了大幅振荡，超调量增大且调节时间变长，而由DSWPI控制的系统仍保持稳定，超调量和调节时间几乎没有发生变化。由此可知，与常规PID控制器相比，动态权值调整法的抗干扰能力更强，适应二冷控制系统突变的能力更好。

图4 拉速2.2m/min时响应曲线

3.2.2 鲁棒性验证

以拉速为1.8m/min时的过程模型为被控对象，调整DSWPI控制器的控制参数使系统响应曲线达到最佳。此时，不改变控制器参数，而是将被控对象变成拉速分别为2.0m/min和2.2m/min下的过程模型，得到三者的系统响应曲线，如图5所示。

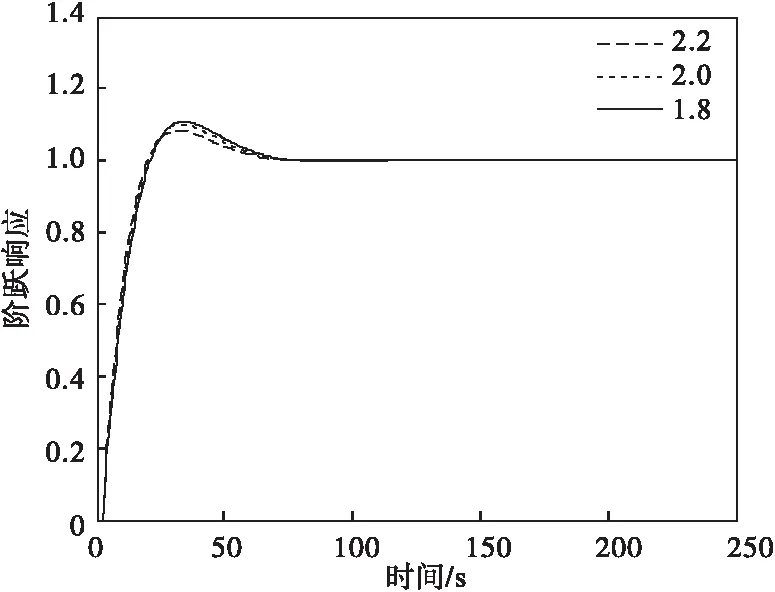
图5 不同拉速下DSWPI响应曲线

由图5可以看出，在控制参数不变的情况下，虽然被控对象发生了变化，但控制器仍保持良好的控制效果。这说明DSWPI控制器在系统参数发生变化时仍能有效的保持系统稳定，模型适配能力较强，鲁棒性良好。

4 结论

针对连铸二冷动态控制问题，基于在线凝固传热模型建立了连铸二冷过程模型；以方坯铸机为对象研究并改进了适用于二冷动态控制的PID动态权值调整法；将动态权值调整法与常规PID控制进行仿真对比。实验结果表明：经过改进的自适应PID动态权值调整法在拉速突变时能在线实时调整控制参数来适应系统的变化，具有良好的模型适配能力和抗干扰能力，比常规PID稳定，鲁棒性更强。

参考文献：

[1] Santos C A,Spim J A,Ierardi M C F,et al.The use of artificial intelligence technique for the optimization of process parameters used in the continuous casting of steel[J].Applied Mathematical Modelling,2002,26(11):1077-1092.

[2] 孙韶元,李世平,王俊然,等.连祷二冷控制的智能化方法[J].北京科技大学学报,1997,19(4):188-191.

[3] Dussud M,Galichet S,Foulloy L P.Application of fuzzy logic control for continuous casting mold level control[J].Control Systems Technology,IEEE Transactions on,1998,6(2):246-256.

[4] Tirian G O,Pinca C B,Creistea D,et al.Application of fuzzy logic in continuo-us casting[J].WSEAS Transactions on Systems and Control,2010,5(3):133-142.

[5] Camisani-Calzolari F R,Craig I K,Pistorius P C.Quality prediction in continu-ous casting of stainless steel slabs[J].Journal of the South African Institute of Mining and Metallurgy,2003,103(10):651-665.

[6] 陈伟,张玉柱,王宝祥,等.连铸二冷参数的优化和控制研究[J].钢铁,2007,42(3):25-29.

[7] Hang CC,Astrom KI,Ho WK.Refinements of Ziegler-Nichols tuning formula[J].IEE Proc-D,1991,138(2):111-118.

[8] Hang CC,Cao L.Improvement of transient response by means of variable setpoint weighting[J].IEEE Trans Industrial Electronics,1996,43(4):477-484.

[9] Dey C,Mudi RK,Lee TT.Dynamic set point weighted PID controllers[J].Control Intelligent Sys,2010,37(4):212-219.

[10] Leva A,Colombo AM.Method for optimizing set-point weights in ISA-PID auto-tuners[J].IEE Proc Control Theory App,1999,146(2):137-146.

[11] Prashanti G,Chidambaram M.Set-point weighted PID controllers for unstable systems[J].J Franklin Tnstitute,2000,337(2-3):201-215.

[12] Chidambaram M.Set-point weighted PI/PID controllers[J].ChemEngComm,2000,179(1):1-13.

[13] Padma Sree R,Chidambaram M.Set-point weighted PID controllers for unstable systems[J].ChemEngComn,2005,192(1):1-13.

[14] 纪振平.连铸二冷动态优化控制与控制系统可靠性研究[D].沈阳:东北大学,2008.

[15] Rajani K.M,Chanchal D.Performance improvement of PI controllers through dynamic set-point weighting[J].ISA Transactions,2011(50):220-230.