基于VGLPV极点配置的非完整机器人轨迹跟踪鲁棒H∞ 控制

郭海峰，鲁宁波

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

由于移动机器人在深空探测、安全与搜救、采矿、农业、林业、物流以及军事等领域有着广阔的应用前景，近年来已经发展成为研究的热点[1-7]。在移动机器人轨迹跟踪的理论研究中，一般假设轮子与地面间只发生纯滚动无侧向和纵向滑动运动，这种理想假设使轮式移动机器人成为一种典型的多输入多输出的非完整约束动力学系统。另外在工程实践中，移动机器人轨迹跟踪控制问题存在大量的不确定性，如由于负载变化导致机器人平台的质量及惯性参数的不确定、因磨损等导致机器人结构参数的不确定以及外部干扰的不确定性等，这使得非完整机器人系统是一类高度非线性、强耦合、欠驱动、时变的动力学不确定系统，难以找到一种通用的、效果较好的控制方法实现其运动轨迹跟踪控制。目前的研究主要有自适应控制、滑模变结构控制、模糊控制、神经网络等智能控制方法[1-7]，虽然在特定情况下取得较好的控制效果，但各种方法都有其局限性，如自适应控制具有固定的结构和可变的参数，对结构不确定性有较好的适应能力,但却无法解决非结构不确定性问题[1]。处理这种具有外部干扰条件和内部参数摄动的复杂不确定非线性的非完整机器人系统，鲁棒H∞控制理论具有一定的优势。而非线性系统的控制问题很多时候可以转化为变增益控制问题，这种方法在航空航天领域已经得到应用[8-9]。此方法首先设计局部控制器,然后在已有局部控制器的基础上综合得到全局控制器。近年来，由于鲁棒控制的不断发展，变增益控制也得到一定的发展，其中线性变参数(Linear parameter varying,LPV)方法已经得到实际应用[9]。

本文针对非完整机器人非线性动力学模型，在外部扰动和内部参数摄动情况下进行鲁棒H∞控制设计，使得机器人轨迹跟随理想轨迹。本文的主要工作：1)根据Euler- Lagrange方程建立非完整移动机器人的动力学模型；2) 确定非完整机器人的运动范围，利用变增益LPV凸分解技术，将这一动态模型转化为具有凸多面体结构的LPV模型；3) 根据鲁棒控制理论和线性矩阵不等式理论，在凸多面体的各个顶点设计变增益控制器，然后利用各个顶点控制器综合得到全局变增益控制器； 4) 最后给出一个仿真算例。结果表明,对于非完整机器人轨迹跟踪问题，这种算法得到的控制器具有较好的跟踪性能。

1 非完整移动机器人的模型

图1为非完整机器人结构。

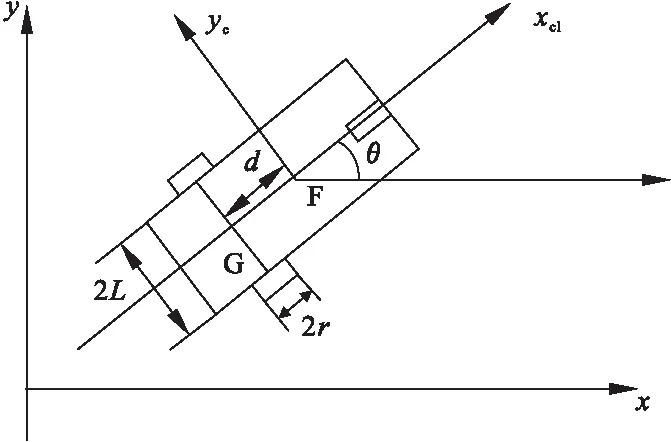
图1 非完整移动机器人的结构

图1所示非完整移动机器人包含一个前面的随动轮和后面两个安装在同一个轴上的差速驱动轮，分别由两个直流电机驱动。使得移动平台直行或转弯。机器人关注点的广义位置坐标q=[x,y,θ]T,两个轮子有相同的半径r，两个驱动轮的距离为2L；F为移动平台的关注点，其坐标为(xF,yF)，G为两轮轴线的重点，G点的坐标为(xG,yG)；左右轮的力矩分别为τl、τr， G点与F点的之间的距离为d。

1.1 移动机器人的运动学模型

根据图1，可知F、G两点的位置存在如下关系

(1)

根据(1)可以得到两点的速度关系

(2)

假设移动平台在低速状态下运行，且驱动轮与地面之间仅有滚动无滑动。那么F点的速度满足以下约束方程

(3)

写成矩阵形式

(4)

式中，AT(q)=[sinθ-cosθd]，

根据文献[2]，推导出移动平台关注点速度以及平台转动角度与左右轮速度之间的运动方程。

(5)

式中vl、vr分别为左轮和右轮的速度。

通过(5)式，可得到关注点F的速度与左右轮速度的关系及其雅克比矩阵。

(6)

将(6)式写成如下形式

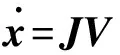
(7)

J是左右轮转速到移动平台关注点速度的雅克比矩阵，反映了轮子转速与关注点速度之间的关系。

1.2 移动机器人的动力学模型

直接应用拉格朗日方程不能得到关于非完整约束的机器人动力学方程。通常，非完整移动机器人有n个广义坐标，且服从m维约束，通过修正后的拉格朗日方程可以得到机器人的动力学模型[3]

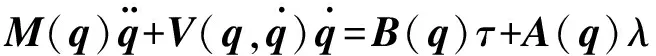
(8)

式中：M(q)∈Rn×n是正定的对称惯量矩阵，

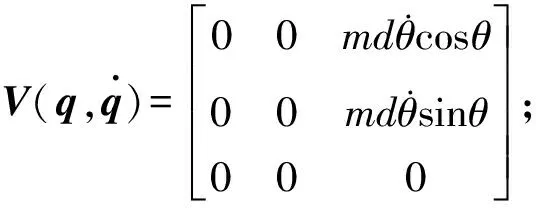
B(q)∈Rn×r是输入转换矩阵，

τ∈Rr×1是输入向量；A(q)∈Rn×m是与约束相关的矩阵；λ∈Rm×1是约束力项。

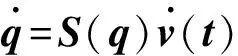
(9)

矩阵S(q)包含了AT(q)零空间的基向量，基向量的选择很重要，这里令速度矢量有实际意义，分别取左轮和右轮的速度，所以S(q)选取如下

(10)

对式(9)两边取微分得

(11)

将式(11)带入到式(8)，两边同时左乘ST(q)得到下式

(12)

式中：

所以式(12)简化为下式

(13)

式(6)带入到式(13)，可得到关注点F的加速度与力矩之间的关系

(14)

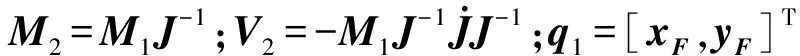
式(14)中M2、V2依赖于参数θ。所以处理后的系统是一个参数依赖系统，这为后面的控制器设计提供了极大方便。

1.3 移动机器人的LPV模型

本文控制目标是移动平台的关注点的轨迹能够跟踪参考轨迹，对系统(14)设计如下控制器

(15)

式(15)带入到式(14)，有

(16)

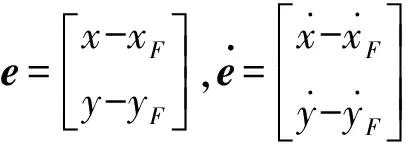
状态方程为

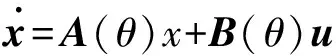
(17)

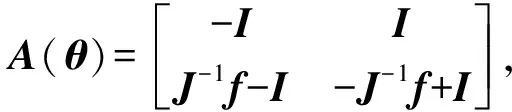
考虑文献[9]的方法，由于矩阵A、B都依赖于参数θ，其范围是：0≤θ≤2π，所以取0和2π作为顶点，利用LPV方法对式(17)进行处理得到

(18)

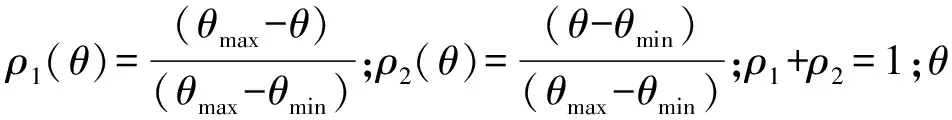
2 变增益LPV鲁棒H∞控制器设计

首先给出LMI区域的定义。

定义1[10]对复平面区域D，如果存在矩阵LT=L∈Rm×m和矩阵M∈Rm×m满足以下条件

D={s∈C∶fD(z)<0}

则称D是一个以fD(z)为特征函数的线性矩阵不等式区域(LMI区域)。其中，fD(z)是埃尔米特矩阵。实际上LMI区域就是一个线性矩阵不等式的可行解区域。

下面对于任意的LMI区域D，将移动机器人的LPV模型在顶点处设计满足极点配置的控制器。对于式(18)分别在θ=0和θ=2π设计满足极点配置和H∞性能要求的状态反馈增益矩阵K1、K2，则对于任意的θ，可利用以下方法得到相应的控制器：

K=ρ1(θ)K1+ρ2(θ)K2

(19)

在每个顶点的位置，LPV模型退化为LTI模型

(20)

式中：w为机器人的外部扰动，这里令其为参考轨迹；z为误差输出，要求机器人能够准确跟踪参考轨迹，既要求在w输入下，z具有H∞性能。

对于系统(20)，设计一个状态反馈控制器

u=Kx

(21)

将式(9)带入到式(8)中，得到闭环控制系统

(22)

则系统(10)的闭环传递函数为

Twz=(sI-A-B2K)-1B1

(23)

本文的目的是设计状态反馈控制器(21)满足以下两个条件：

1) 闭环极点配置到一定的LMI区域；

2) 保证闭环系统H∞性能‖Twz‖∞<γ，γ为给定常数。

为取得满意的性能，这里将闭环极点配置要求α=2(在复平面-2的左边)，这样可以保证衰减速率。XD是正定矩阵，根据特征函数可以得到描述该区域的线性矩阵不等式

(A+B2K)XD+XD(A+B2K)T+2αXD<0

(24)

有界实引理[10]：假设γ>0，设计的控制器(21)要求满足以下性质：

1)闭环系统内稳定并且

‖TwZ‖∞=‖(SI-A-B2K)-1B1‖∞<γ。

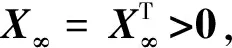
(25)

成立。

定理：对于系统(20)，给定γ>0，∃XT=X>0，和矩阵W=KX，满足以下不等式约束

(A+B2K)XD+XD(A+B2K)T+2αXD<0

如果X*和W*为上述不等式的可行解，则系统的状态反馈控制器为u=W*(X*)-1x，该控制器不仅可保证H∞性能，且可以保证把闭环系统的极点配置到相应的区域。

用LMI中的feasp来求解该线性矩阵不等式。

根据以上所述，在顶点处综合局部控制器，根据式(19)可得到任意θ的控制器。

3 仿真算例

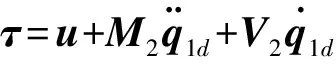
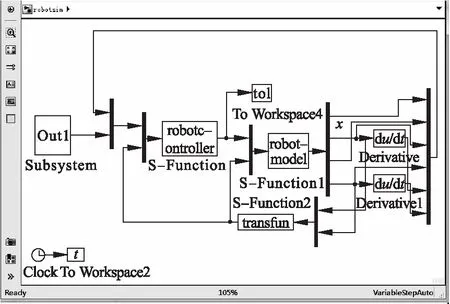
图2 主仿真界面

图3 子系统界面

相关参数如表1所示。

表1 移动机器人的参数

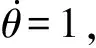
K2=

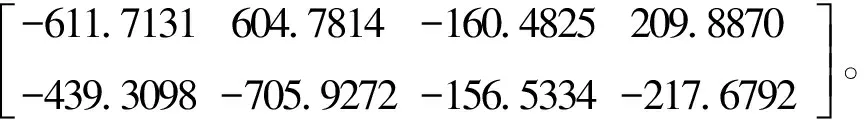
以及与定点相对应的闭环极点

(-3.8535±3.5438i),(-2.8004±0.8134i)

由以上两个反馈增益矩阵，通过式(19)得到整个LPV变增益反馈矩阵，通过在线计算ρi(i=1,2)，可得到具体位置的增益反馈矩阵

K=ρ1(q)K1+ρ2(q)K2，且ρ1+ρ2=1

据以上所述，得到系统的变增益控制器u=Kx。

在仿真中，移动机器人末端理想轨迹方程为xd=cos(t)和yd=sin(t)，根据本文所提出的方法设计控制器，机器人在x、y方向的运动轨迹如图4所示。

图4是机器人在参考输入下，分别在x、y方向的运动轨迹方程。图5给出两关节控制器输出控制力矩的响应曲线。图6显示移动机器人轨迹跟踪曲线，关注点轨迹的相应曲线基本与参考轨迹重合，图6中实线为实际运动轨迹，虚线为参考轨迹。结果表明，采用这种控制方法，移动机器人关注点的位置变化具有良好的跟踪性能。

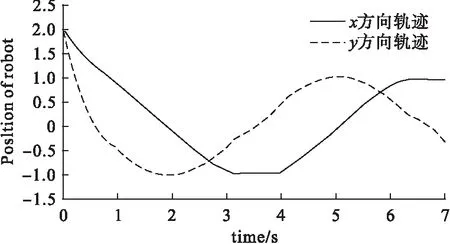
图4 机器人在x、y方向的运动轨迹

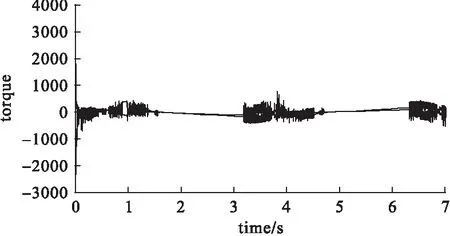
图5 两关节控制力矩响应曲线

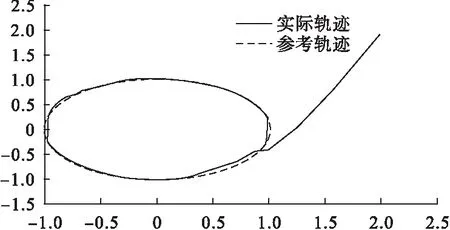
图6 机器人轨迹跟踪曲线

4 结论

移动机器人轨迹跟踪模型中存在动态不确定性和外部干扰的不确定性，使得模型具有时变、强耦合、非线性等复杂的动力学特性。本文引入变增益LPV鲁棒H∞控制方法，设计了移动机器人轨迹跟踪控制器。仿真结果表明：机器人手臂关节位置的变化始终具有良好的跟踪性能。

参考文献：

[1] 吴忻生,任华瑛.非完整移动机器人轨迹跟踪的最优模糊控制[J].华南理工大学学报：自然科学版,2004,32(3):44-49.

[2] Das T,Kar I N.Design and implementation of an adaptive fuzzy logic-based controller fo-r wheeled mobile robots[J].IEEE Transactions on Control Systems Technology,2006,14(3):501-510.

[3] Lih-chang Lin,Hao-yin Shih.Modeling and Adaptive Control of an Omni-Wheeled Robot[J].Intelligent Control and Automation,2013(4):166-179.

[4] 吴菁,陈罡,孟静.基于预测控制的非连续路段下移动机器人的轨迹跟踪[J].计算机测量与控制,2016,24(10):74-78.

[5] 郑伟勇,李艳玮.基于前馈-反馈的移动机器人轨迹跟踪控制[J].计算机工程与设计,2017,38(2):539-543.

[6] 康升征,吴洪涛.全向移动机器人模糊自适应滑模控制方法研究[J].机械设计与制造工程,2017,46(3):70-75.

[7] 叶锦华,吴海彬.不确定轮式移动机器人统一自适应神经网络H∞控制[J].中国机械工程,2017,28(2):150-155.

[8] 张弛,王向东.多项式LPV模型的航空发动机变增益切换控制研究[J].科技创新与应用,2017(6):99-100.

[9] 虞忠伟,陈辉堂,王月娟.基于LMI方法的机器人LPV鲁棒H∞控制器设计[J].控制与决策,2001,16(2):146-150.

[10] 俞立.鲁棒控制:线性矩阵不等式处理方法[M].清华大学出版社,2002.

[11] Gahinet P,Apkarian P.A linear matrix inequality approach toH∞control[J].Int J Robust Nonlinear Control,1994,4(3):421-448.