逻辑斯蒂回归模型在电信领域中的应用

金海月

(沈阳理工大学 信息科学与工程学院，沈阳 110159 )

电信规模庞大、纷繁杂乱的历史数据的背后隐藏着很多具有决策意义的有价值的信息，如何利用这些对电信经营决策有用的信息，已成为电信行业的当务之急。目前国内电信运营商基本完成了企业级数据仓库的设计与建设。随着全业务运营时代的到来,产品日益同质化,各大运营商的客户流失问题渐显；同时随着全球电信市场进入高速增长阶段,用户开始流动迁移,如何维系客户关系,保持客户粘性，使现有客户由于工作需要或个人意愿需要更换现有业务时,仍然选购当前运营商的服务，成为企业和学者关注的问题之一。文献[1]采用多任务学习方式，主要通过对不同任务域之间的共性特征进行寻找并共享而完成,而对于不同任务域的学习来说,采用知识迁移加速的方式可以为每个任务域构建分类器。文献[2]从理论上证明了通过构造多任务分类器的“开销函数”和“差异性度量函数”，MTC-LR 算法可以提高多任务分类器的各自分类精度。

本文通过分析电信领域用户的类别特点，导出逻辑斯蒂回归模型，研究电信领域中新服务的接受率问题。

1 逻辑斯蒂回归[3-5]

一般说的逻辑斯蒂(Logistic)回归，是指二分类问题。

对于连续的变量x，假设其服从逻辑斯蒂回归，设定u、b、γ、h为多元线性回归模型的未知常数,x是线性模型的基函数，则

(1)

(2)

对应概率密度以及分布函数如图1所示。

图1 概率密度及分布函数图

定义逻辑斯蒂回归模型：

x∈Rn为输入，Y∈{0,1}为对应输出，二项逻辑斯蒂回归对应如下模型：

(3)

(4)

为表示方便，记参数向量为W。

w=(w(1),w(2),…,w(n),b)T，x=(x(1),x(2),…,x(n),1)r,则表达式简化为

(5)

(6)

式(5)、式(6)是一个线性回归的表达式。

参数的求解，就是求解w，利用最大似然估计求解。

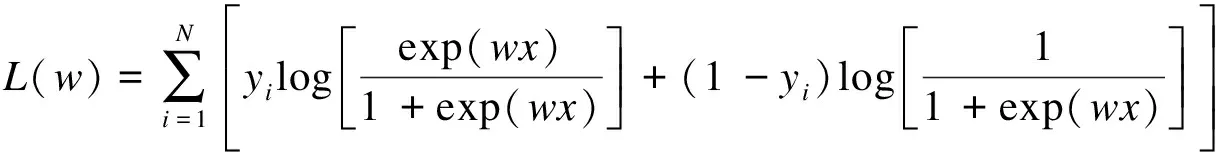
(7)

定义sigmoid函数：

(8)

准则函数重新写为：

(9)

准则函数可以借助梯度下降或牛顿法求解。

利用求解得到的w，即可以进行概率判断，哪个概率大既判给哪个类别。概率判断可据式(10)和式(11)。

(10)

(11)

2 逻辑斯蒂回归

逻辑斯蒂回归拓展了多元线性回归的思想，处理因变量y是二值的情况(为简单起见，通常用0和1对这些值编码)。和多元线性回归一样，自变量x1、x2、x3、…、xk可以是分类变量、连续变量或二者的混合类型。

2.1 算法应用

算法中采用的仿真数据来自AT&T公司在美国的调查，样本数据(新服务)中总体接受新服务的概率是1628/10524=0.155。但是，接受新服务的概率因教育、居住稳定性和收入等自变量的类别不同而异；最低值是0.069，来自低收入、无迁居并且受过某种高等教育的家庭；最高值是0.270，来自高收入、有迁居并且受过某种高等教育的家庭，如表1所示。标准多元线性回归模型不适合对这种数据建模，原因如下：

(1)模型的预测率可能会超过0～1的范围。

(2)因变量并非正态分布。事实上，二项式模型更合适。例如：如果一个单元共11个住户，则该变量只能取11个不同值0，1，2，3,…,11。设定单元中家庭的响应通过随机掷硬币确定，正面朝上代表接受，正面朝上的概率随单元变化。

(3)如果认为正态分布是二项式模型的近似，则在所有的单元中，因变量的方差不是常数：对于接受新服务的概率p接近0.5的单元，方差比p在0或1附近的那些单元高。该方差还随一个单元的住户数增加而增加，且等于n(1-p)本质上，消费者理论是说当一个消费者面临一组选择时，其所做的选择具有最高的效用(效用是以任意的零点和尺度对价值的量化度量)。假定消费者对选择列表有一个倾向性排序，而这一排序满足一些合理的标准，如传递性。倾向性排序可以基于个体(如调研中的社会经济特征)或所做选择的属性。随机效用模型认为一个选择的效用是纳入一个随机元。当对一个随机元建模，假设其来自于一个“合理的”分布时，可以逻辑地导出预测选择行为的逻辑斯蒂模型。

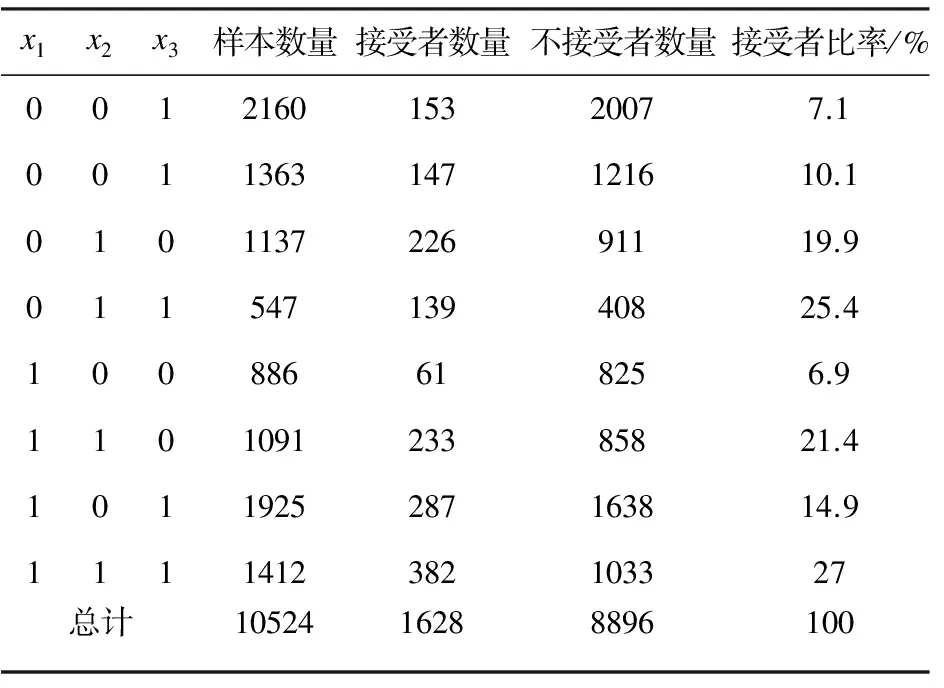
表1 逻辑斯蒂回归模型分析的数据格式 个

2.2 逻辑斯蒂建模

如果以Y=1表示选择一个选项，Y=0表示不选择该项，则逻辑斯蒂回归模型定义为

式中β0、β1、β2、β3、…、βk是类似于多元线性回归模型的未知常数。模型中的因变量是

x1=(教育：高中或以下=0，大专或以上=1)；

x2=(居住稳定性：近五年没变化=0，近五年有变化=1)；

x3=收入(低=0，高=1)。

表1中的数据是以回归程序所要求的典型格式组织。

AT&T的逻辑斯蒂模型是：

通过下面的式子得到系数的有用解释：

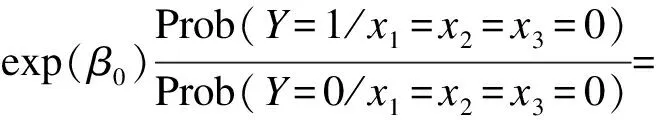
逻辑斯蒂模型是下面形式的几率乘积：

对于给定的x1、x2、x3，接受新服务的几率=exp(β0)×exp(β1x1)×exp(β2x2)×exp(β3x3)={基本情况的几率}×{关于x1的因子}×{关于x2的因子}×{关于x3的因子}

如果x1=1,那么无论x2和x3的取值如何，接受新服务的几率都将被乘以相同的因子；同样，关于x2和x3的因子也不随其他变量的取值而改变。变量的这个因子说明了该变量的存在对接受新服务的几率的影响。

如果βi=0，那么相应(变量)的因子没有作用(乘以1)。如果βi<0,则(变量)因子降低了接受新服务的几率以及概率；而当βi>0时，(变量)因子增加了接受新服务的概率。

3 实验仿真分析

本次调查旨在分析4G网络技术体系情况下，广大用户对4G手机产品、4G可视电话增值服务业务的选择，为手机厂商、电信运营商和增值服务提供商针对4G产品和服务提出较为有效的建议。

接受新服务概率的最大似然估计值需要经过计算机程序的迭代计算。设置95%置信区间一个典型的计算机程序的输出结果见表2。

根据系数的估计值，对于自变量的家庭，接受4G新服务的估计概率

Probability(Y=1|x1,x2,x3|)=

用该模型估计采用4G新服务的家庭个数是具有自变量值x1、x2、x3的家庭总数乘以以上的概率。表3给出了自变量取值的各种组合所对应的接受新服务估计值，常数β0取值-2.5，标准差为0.058。

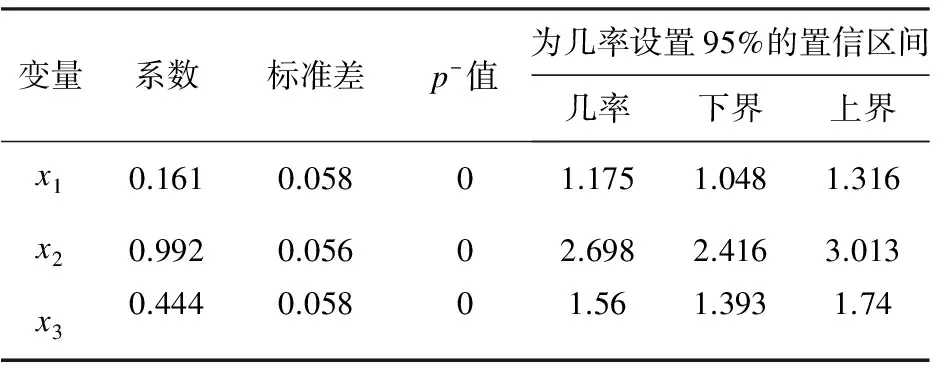
表2 逻辑斯蒂回归分析的输出

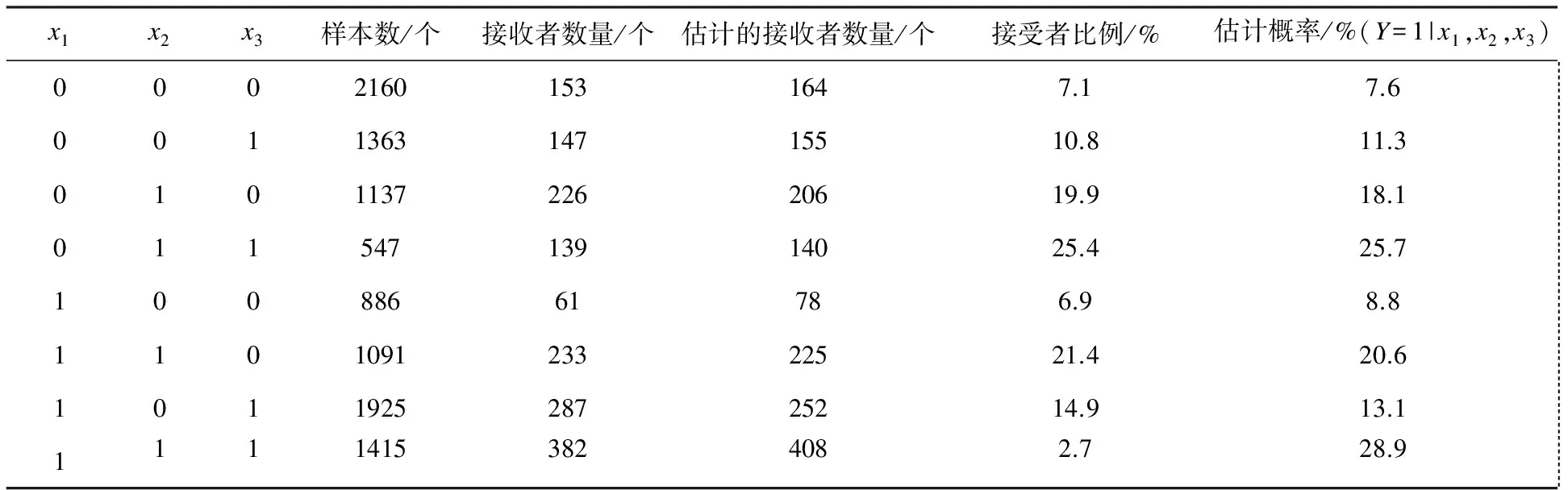
表3 基于逻辑斯蒂回归模型的估计输出

将拟合模型中没有使用的保留数据作为验证数据，有598个用户组成了验证数据，见表4所示。

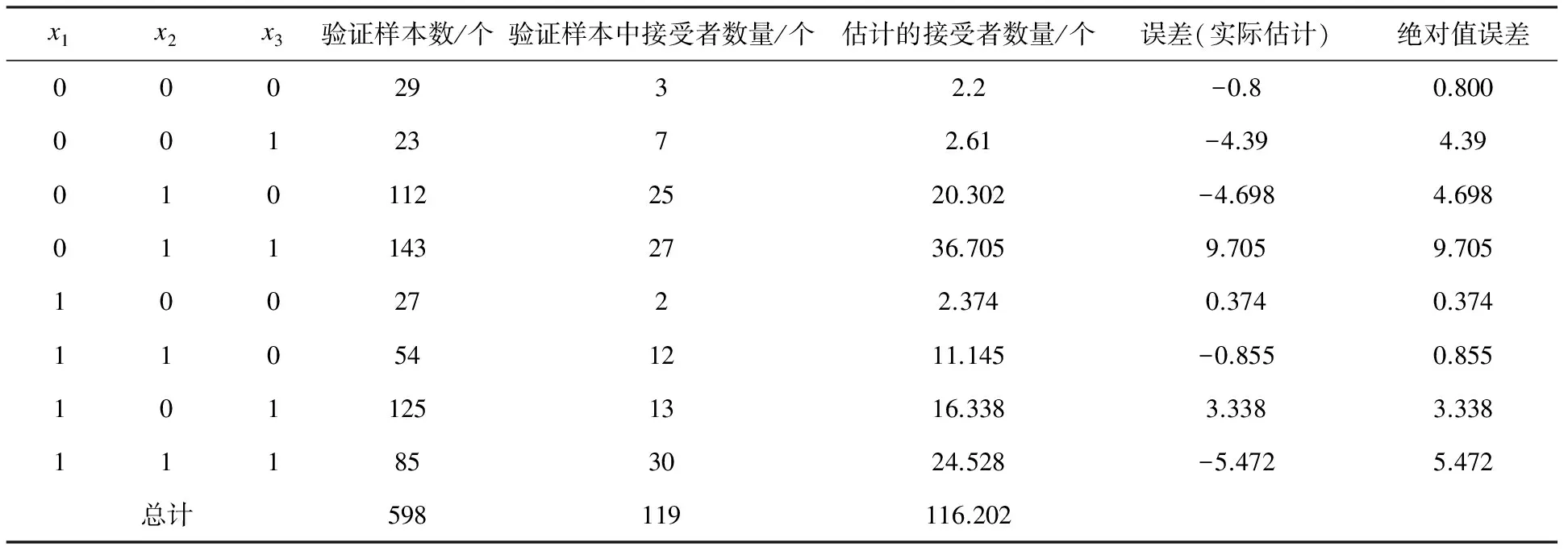
表4 检验数据

总体误差是-2.8/119=-2.3%，平均绝对值误差比是：

(0.800+4.390+4.689+9.705+0.374+0.855+3.338+5.472)/119=0.249=24.9%。表5列出了验证数据集的用户家庭的混淆矩阵。

表5 混淆矩阵

和多元线性回归一样，可以引入由相互作用的新因子来构建更复杂的模型来反映自变量之间的相互影响。例如，如果认为x1和x2之间存在相互影响的效果，可以增加相互影响项x4=x1×x2

4 结束语

逻辑斯蒂回归模型拓展了多元线性回归的思想。通过设置电信领域中注册用户的类别分类，设计了罗杰斯谛回归模型。将仿真数据设计为回归模型中所要求的典型格式，利用二阶导数牛顿法迭代出最大似然估计，求解出最优解。实验证明，逻辑斯蒂模型在实际应用过程中具有预测率高，关键变量选取准确的特点。

参考文献：

[1] 陈倬.基于逻辑回归的多任务域快速分类学习算法[J].数字技术与应用,2016(11):123-123.

[2] 顾鑫,曹丹华,吴裕斌,等.基于逻辑回归的多任务域快速分类学习算法[J].计算机工程与应用,2017(15):47-56.

[3] 张鹏丽,李育.逻辑斯蒂模型在河谷型城市洪水事件研究中的验证[J].西北师范大学学报：自然科学版,2017,53(1):128-134.

[4] 杨波，余建星，王谦.逻辑斯蒂增长模型在集装箱运量长期预测中的应用[J].海洋技术,2006,25(4):88-93.

[5] 梁慧玲,王文辉,郭福涛,等.比较逻辑斯蒂与地理加权逻辑斯蒂回归模型在福建林火发生的适用性[J].生态学报,2017,37(12):4128-4141.