模糊控制应用于伺服系统PID自整定的研究

叶海平

(漳州职业技术学院 机械与自动化工程系 福建 漳州 363000)

在现代工业过程控制中，PID控制由于结构简单，操作方便，稳定性好，适应性强等优点而受到广泛应用。数控机床伺服系统的参数控制也是利用PID的控制器。随着智能制造和工业4.0的进一步推广，对数控机床的整体性能提出了更高的要求。作为数控机床的核心部件，伺服系统在运行过程中的稳定性、响应能力、适应性和抗干扰能力都要增强。采用传统的PID控制方法已经不能满足数控机床伺服系统的发展需求。[1-2]

随着数控技术的不断发展，伺服控制系统变得更加复杂，难以精确地运用数学模型来描述。而传统的PID控制器只适用于精确的控制系统动态模式。随着科学技术的发展和数学优化算法的不断深入研究，模糊控制成为自动控制领域一个非常活跃而又硕果累累的分支，广泛应用于工业过程控制。模糊控制不依赖于被控对象的精确数学模型，特别适用于控制非线性、时变、滞后、模型不完全的系统。因此，可以尝试以模糊控制来处理伺服系统的PID控制在线自整定问题。[3]

PID控制的三个参数设定决定了伺服系统的性能，本文将模糊控制理论应用到PID控制器在线自整定，使得控制器能够根据外部环境的变化，进行在线整定优化出参数值，大大提高了伺服系统的整体性能。

1 模糊自整定PID控制器的设计

PID控制器包含有三个单元，分别是比例单元、积分单元和微分单元，通过这三个单元做出及时的反馈，实现对控制对象的在线纠正。需要控制的对象有Kp、Ki和Kd三个参数，三个参数分别是比例系数、积分系数和微分系数，三个参数的选择决定了整个控制系统的整体性能。模糊PID控制器的工作原理就是基于控制系统的工作原理和控制参数，采用模糊控制技术，确定PID控制器的Kp、Ki和Kd三个参数，使得控制系统的性能得到最优化。其工作原理如图1所示。

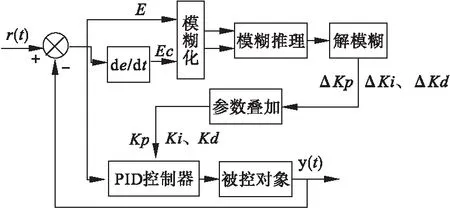
图1 模糊PID控制器工作原理图

1.1 模糊化计算

由图1模糊PID控制器控制器工作原理，可以确定输入参数变量有系统误差E和误差变化率Ec。模糊控制的输出变量分别是ΔKp、ΔKi、ΔKd。根据模糊分割理论，确定分割数为{NB,NM,NS,Z,PS,PM,PB}。输入变量系统误差和系统误差率的论域{-4,-2,-1,0,1,2,4}，输入变量的论域为{-4,-2,-1,0,1,2,4}。由于三角形函数的结构简单，响应快，适用于模糊控制器的在线调整。因此,选择三角形函数来描述变量的隶属度曲线，图2为输入变量的隶属度函数曲线，图3为输出变量的隶属度函数曲线[4-5]。

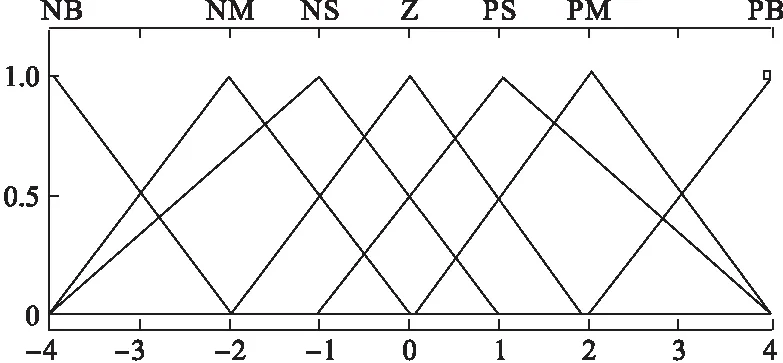
图2 E和Ec的隶属度函数曲线

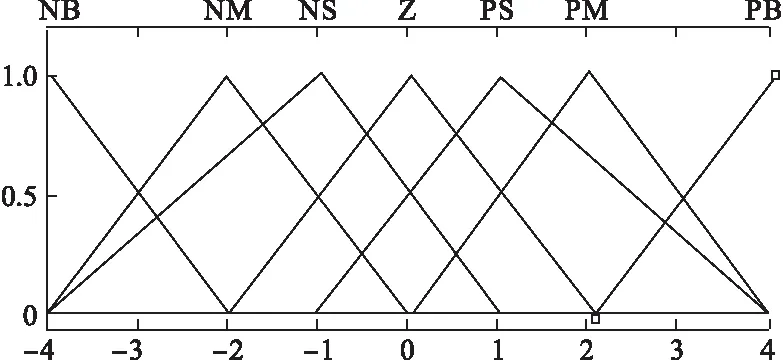
图3 ΔKp、ΔKi 和ΔKd的隶属度函数曲线

1.2 建立模糊规则表

根据PID控制器的工作原理，当系统误差变化，为保持系统能够稳定地运行，应该相应的增加比例系数Kp和积分系数Ki。在调整时，为避免系统在调整之后出现较大的超调或震荡，以及系统在设定值附近出现振荡，当Ec的值偏小时，应该适当增大比例系统Kd；当Ec值偏大时，应该适当地减小Kd。结合PID参数整定，当系统的误差率发生变化，PID的参数应该做出相应调整。不断地调整实验，整理得到输出变量Kp、Ki、Kd的控制规则如表1、表2、表3 所示[6-7]。

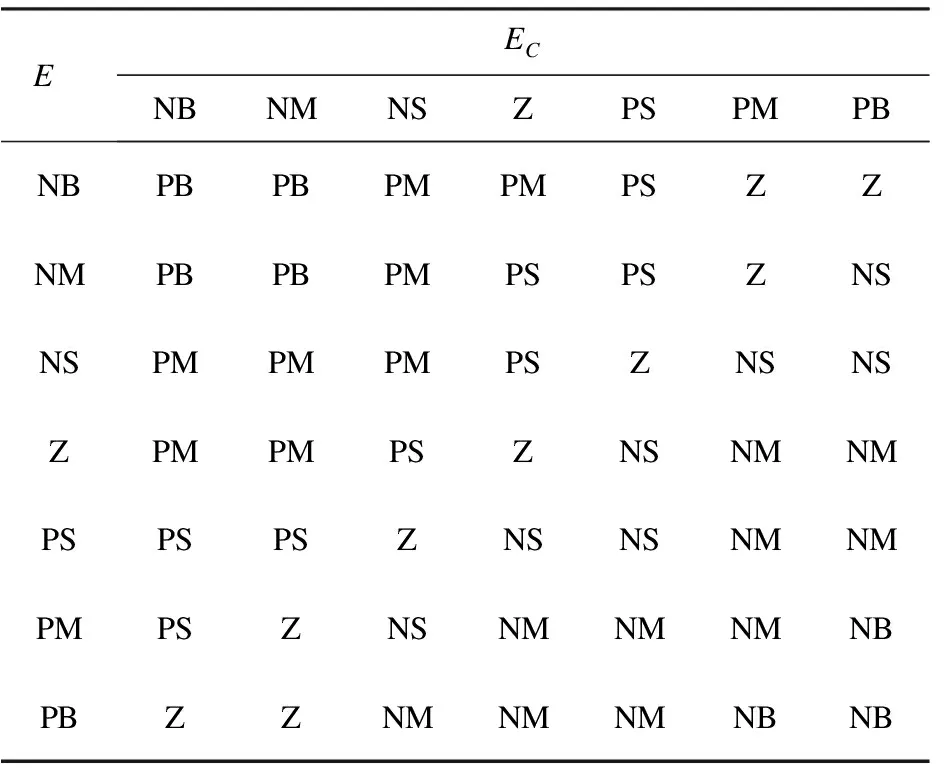
表1 Kp控制规则表

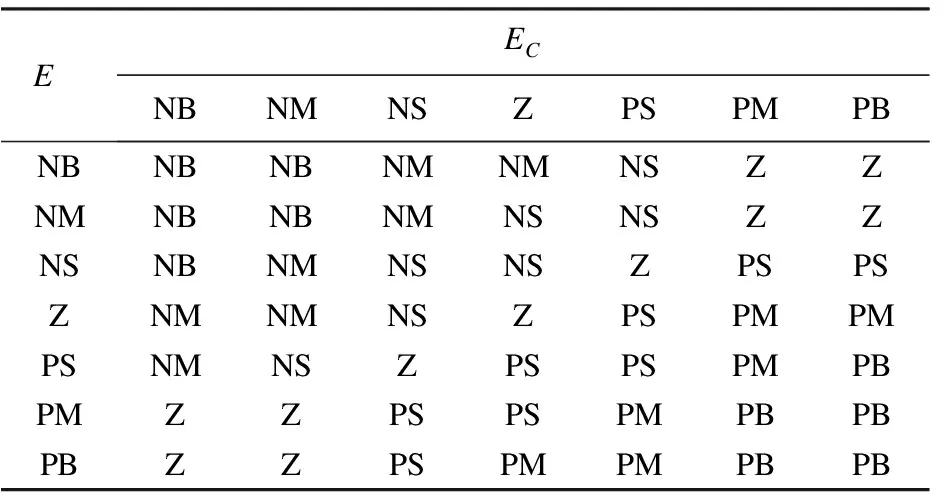
表2 Ki控制规则表

表3 Kd控制规则表

模糊控制器的3个参数Kp、Ki、Kd的表达式为

Kp=kp0+{E,EC}p

Ki=ki0+{E,EC}i

(1)

Kd=kd0+{E,EC}d

kp0、ki0、kd0为3个参数的初值，{E,EC}p、{E,EC}i,{E,EC}d为模糊控制表中的修正值。本文PID控制算式为

(2)

1.3 用模糊控制实现PID自整定

首先，根据变量的隶属度函数和模糊控制规则，利用Matlab软件里的模糊推理系统工具箱的控制器模糊推理系统来建立模糊控制器的模型。

按推理系统的要求分别输入模糊控制的参数、值域、隶属度函数和控制规则等，建立模糊控制的模块。将建好的模糊控制器插入到已经建好的PID控制器当中，形成模糊PID控制器结构图,如图4[8-9]所示。

图4 模糊自整定PID控制器结构图

2 将模糊自整定PID 控制应用到伺服系统进行仿真

以小型数控车床的Z轴伺服控制系统为例， 伺服电机的传递函数为

(3)

根据数控机床伺服系统的相关参数和控制原理图，建立伺服系统的控制结构图。将模糊PID控制器应用到伺服系统的控制当中，在Matlab的Simulink里面构建伺服系统控制结构图,如图5所示。将模糊PID 控制器和传统的PID控制器进行仿真比较。模糊PID控制器的输入是系统输入和反馈输出的差值，输出为模糊控制器整定后的数据，控制参数Kp、Ki和Kd的数值范围为(0，20)。初始PID 参数值均为：Kp=2，Ki=0.1，Kd=0.5。仿真结果如图6所示[10]。

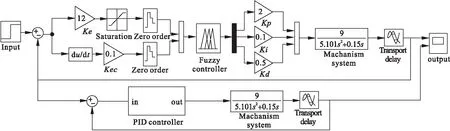
图5 模糊自整定PID控制器

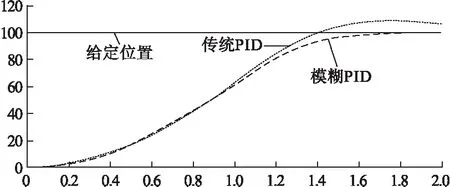
图6 普通PID和模糊PID的控制效果图

图6给出了传统PID控制和模糊PID控制对信号响应的比较。通过观察对比可以看出，模糊PID调节控制方法用了较短时间到达稳定跟随状态，超调量几乎为零。传统PID控制方法用了较长时间才达到稳定跟随状态，超调量较大，且有一定的震荡现象。对比结果可以说明：模糊PID调节控制方法在超调量、上升时间和稳定时间上都优于传统PID的控制方法。

3 结论

将模糊控制理论应用PID控制器的在线自整定中。将设计好的模糊自整定PID控制器应用到数控机床的伺服系统当中，保障伺服系统运行的稳定。在Matlab的simulink软件中，建模仿真实验，并与传统的PID自整定进行比较。仿真结果表明，模糊控制理论应用到伺服系统PID参数的在线自整定当中，模糊PID控制伺服系统的稳定性好，响应时间短，没有出现超调。

参考文献：

[1] Xu Q,He C H,Wang Y L.Study on Optimization Design of PID Parameters Based on Simplex Method[J].Energy Procedia,2011(13)：5396-5401.

[2] Dwyer A O.Handbook of PI and PID Controller Tuning Rules [M].London： Imperial College Press，2009：44-51.

[3] 何佳佳,侯再恩.PID参数优化算法[J].化工自动化及仪表，2010，37(11)：1-4.

[4] Liu X Q,Wang Y,Mu S Y.Design of Optimal Parameters for PID Controller Based on Simplex Search[J].Computer Simulation,2004，21(11)：191-193.

[5] 杨津听,熊浩,丁黎梅.S7-200 PLC的PID自整定算法剖析[J].工业控制计算机，2012，25(1)：9-10.

[6] 傅思萍.改进遗传算法优化自动组卷技术的研究[J].金陵科技学院学报,2015,31(3):56 -62.

[7] Denis Garagic,Krishnaswamy Srinivasan.Adaptive Friction Compensation for Precision Machine Tool Drive[J].Control Engineering Practice,2003(11):1451-1464.

[8] Bernard B.On-line Friction Modeling,Estimation and Compensation for Position Control[D].Florida:University of Florida,2002.

[9] 袭著燕,张涛,路长厚.数控伺服进给系统中摩擦补偿控制研究进展[J].现代制造工程,2006(1):21-25.

[10] 王毅,何肤,苏宝库.摩擦模型的Simulink 仿真[J].电机与控制学报,2004,8(1):60-62.