基于Markov跳变非线性系统的粒子滤波跟踪算法

华宇宁，崔春娜，郝永平，傅国强

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

多目标检测前跟踪技术(TBD)[1]是国际雷达界信号处理领域的前沿研究热点。近年来，海内外学者对检测前跟踪技术进行了大量研究,其中，DP-TBD算法和 PF-TBD 算法的综合性能最佳，本文主要围绕PF-TBD算法来研究。

针对经典粒子滤波算法在红外多目标跟踪，尤其是目标被遮挡时跟踪效果不佳的问题，本文在粒子滤波算法中引入Markov跳变非线性系统[2]，既在贝叶斯估计时引入一种Markov随机场来描述目标交汇时的交汇模型,并将其应用在有目标遮挡情况的红外图像的多运动目标跟踪中，Markov随机跳变非线性系统的特点是结构的不确定性，且状态过程随机，因此非常适用于多运动目标的检测，尤其是目标遮挡这类问题。

1 Markov跳变非线性系统的数学模型

离散Markov标量过程s(t)由状态概率p(s)(t)和从状态k到状态s的转移概率p(sk)(s,t|k,t′)来描述：

p(s)(t)=p(s,t)=p[s(t)=s,t]

(1)

p(sk)(s,t|k,t′)=p[s(t)=s,t|s(t′)=k,t′]

(2)

由式(1)、(2)可知状态概率和转移概率都与系统状态X(t)无关。

随机过程s(t)的转移概率需满足Markov方程[3]：

(3)

具有Markov跳变参数的非线性随机动态过程由下列方程描述：

X(k+1)=X(k)+f(k,X(k),η(k),ε(k),w,X(k0))=X(k0,w)

(4)

式中：X(k)为任意维数空间上的Wiener过程;f(k,X(k),η(k),ε(k),w,X(k0))为具有Markov跳变参数的非线性函数;η(k)、ε(k)、w为马尔可夫参数。

2 引入Markov跳变非线性系统的粒子滤波算法原理

Markov随机场建立在非线性的系统上，由离散的随机变量组成一个二维网格，这二维网格被称为随机场[4]。转移概率需满足式(3)所示的Markov方程。

在多目标跟踪当中，每一个无向图[5]中的节点可以视为一个跟踪目标，目标与目标之间的关系靠节点之间的边来维系，每一个边上都记录着跟踪目标之间概率依赖程度。在Markov随机场中，随机场由链式结构转化为网络结构，将目标与目标之间的相互影响加入多目标跟踪中的网络结构中，这样就解决了多个跟踪目标之间的数据关联问题，从而解决多目标跟踪当中的目标被遮挡问题。多目标跟踪的Markov网络[6]如图1所示。

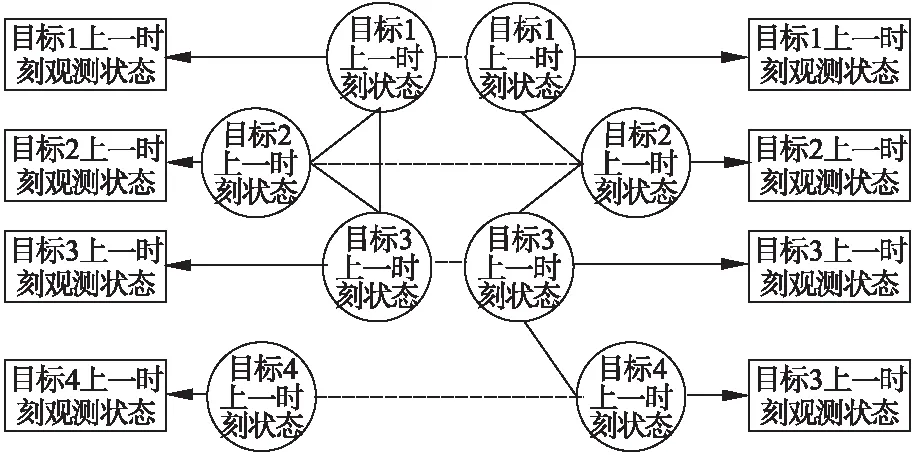
图1 多目标Markov跟踪框图

该Markov网络结构分为两层，状态层和观测层，其中状态节点用圆形表示，观测节点用方形表示。

3 引入Markov跳变非线性系统的粒子滤波跟踪算法的实现

(1)初始化粒子数目及权值

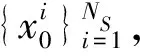
(2)粒子更新

(5)

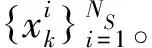
(3) 权值优选重采样

计算k时刻Ns个粒子的权值，提取权值较大的前Np个粒子。

(6)

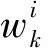
(4)归一化权值

(7)

(5)引入Markov随机场的贝叶斯估计[7-8]，融入Markov网络的贝叶斯估计的观测方程为

Ytk=h(xtk,rtk,tk)+vtk

(8)

式中：k=0,1,…;Ytk是观测向量；xt是变量tk的函数；h(xtk,rtk,tk)是随机动态系统的非线性函数；vtk是零均值的高斯白噪声过程。

从目标i跳变到目标j的状态估计公式可用下式求解。

(9)

式中，1≤i；j≤m；δ为已知高斯函数的协方差。

(6)目标数量估计

(7)权值恢复

跳转到下一时刻，返回步骤(2)

跟踪算法流程图如图2所示。

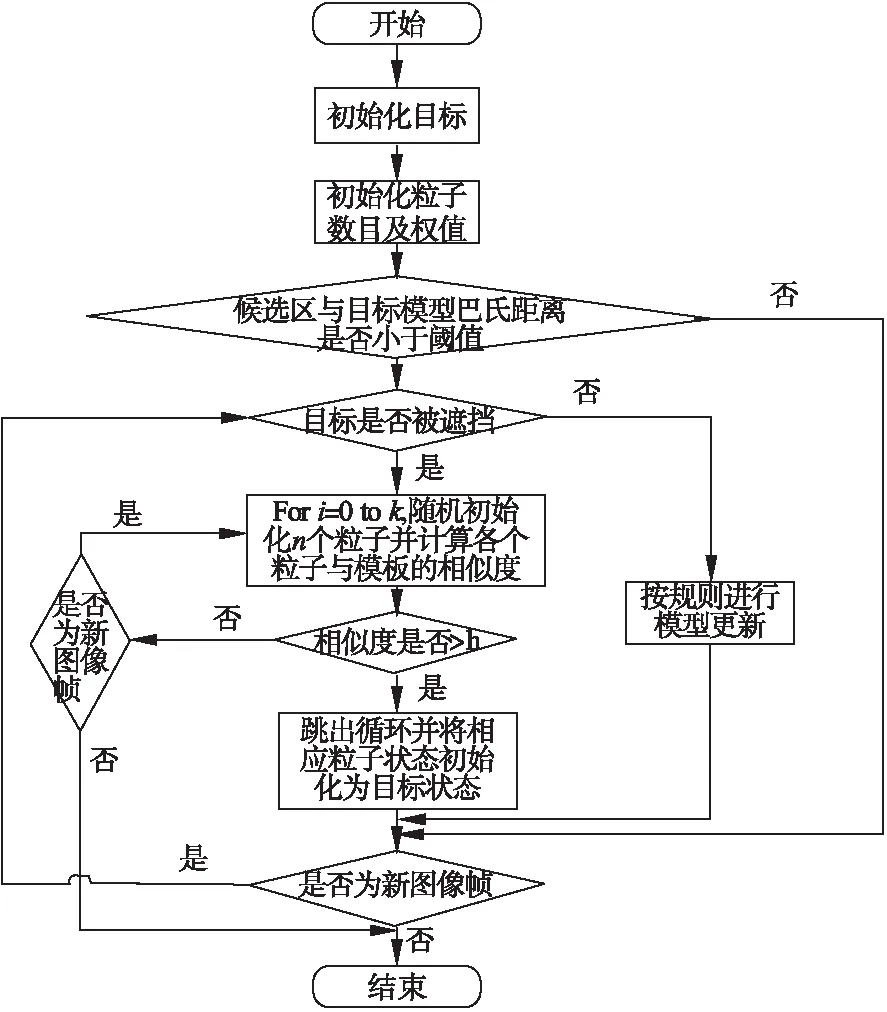
图2 多目标跟踪算法流程图

4 实验结果及分析

将经典粒子滤波算法与本文基于Markov非线性系统的粒子滤波算法的跟踪效果进行对比实验。

实验一：多运动目标被物体遮挡时的跟踪。

红外图像共1650帧，分别抽取有代表性的四帧图像进行对比试验。实验结果如图3、图4所示。

本实验中有多处目标运动过程中出现遮挡的情况，由图3a、3b，图4a、4b可看出：目标在没有被遮挡之前，两种跟踪算法的都能有效地跟踪目标。当跟踪目标发生遮挡时，采用经典粒子滤波算法会丢失跟踪目标，如图3c、3d所示；而使用本文基于Markov粒子滤波算法时，从图4c、4d看出，当目标被部分遮挡或完全遮挡及至目标脱离遮挡物重新出现时，跟踪框都能准确锁定在重新出现的跟踪目标上。这说明，改进后的算法与经典粒子滤波算法相比，有效地提高了粒子滤波算法的抗遮挡能力并保持了跟踪的稳健性。

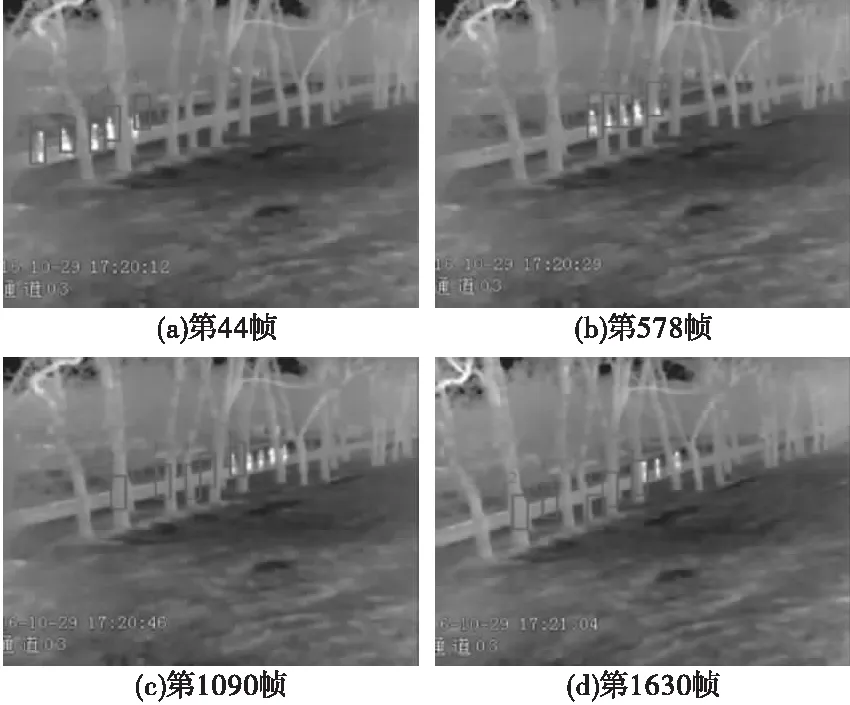
图3 经典粒子滤波算法跟踪效果

图4 基于Markov的粒子滤波算法跟踪效果

实验二：相似目标交叉遮挡实验

在实际应用中，有时会遇到相似目标发生交叉遮挡的现象，也使跟踪难度增加。使用经典粒子滤波算法和本文基于Markov粒子滤波算法分别进行跟踪对比实验，红外图像共720帧，分别抽取其中四帧图像进行说明，如图5、图6所示。

图5 经典粒子滤波算法跟踪效果

图6 基于Markov的粒子滤波算法跟踪效果

本实验跟踪目标是两相似人体目标，在没有发生交叉遮挡之前两种算法都能有效跟踪目标，但当目标发生交叉遮挡时，采用经典粒子滤波算法跟踪丢失了目标2的信息如图5c、5d所示。而采用基于Markov粒子滤波算法时，在发生目标交叉遮挡后能够找到正确的跟踪目标并准确地进行跟踪，如图6c、6d所示。实验表明，使用基于Markov的粒子滤波算法，在跟踪相似目标发生交叉遮挡时，跟踪效果及跟踪准确度优于经典粒子滤波算法。

实验三：跟踪时间对比实验

用粒子滤波算法进行目标跟踪时，粒子数量取170个左右时跟踪效果较好，本组实验选取170个粒子进行跟踪，图7为经典粒子滤波算法、基于均值漂移的粒子滤波算法以及基于Markov的粒子滤波算法的运行时间。

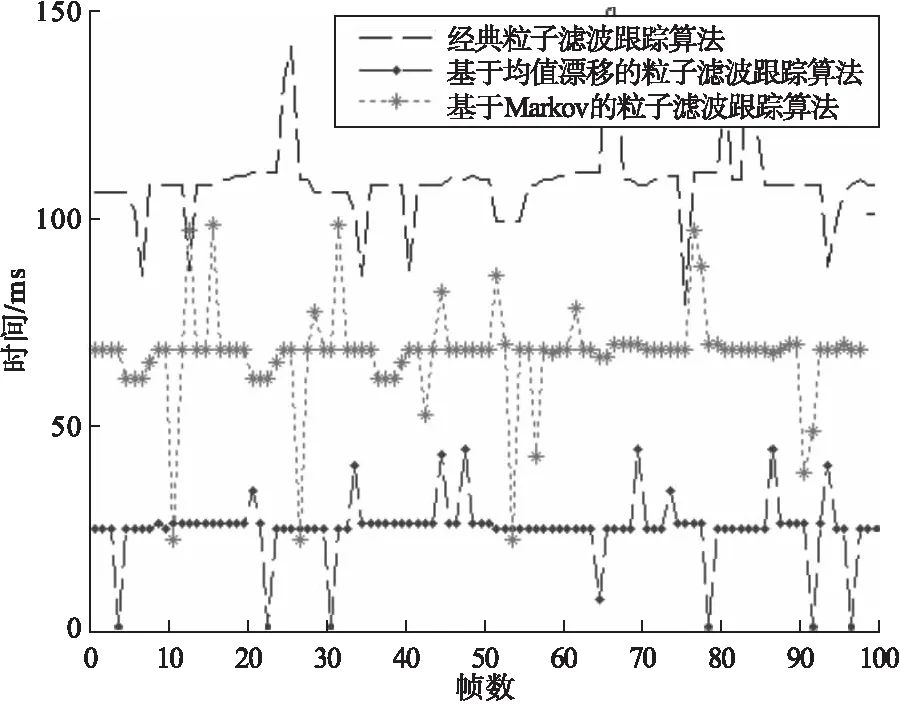
图7 算法跟踪时间对比曲线

由图7可知，基于均值漂移的粒子滤波算法平均耗时为23.44ms，经典粒子滤波算法跟踪时间为107.77ms，基于Markov粒子滤波算法运行时间65.43ms。本文的基于Markov粒子滤波算法与经典粒子滤波算法相比跟踪时间大大缩短，实时性优于经典粒子滤波算法。

5 结论

研究了基于粒子滤波的红外多目标跟踪算法，针对经典粒子滤波算法对于多目标跟踪目标被遮挡时跟踪准确性欠佳的问题，对算法进行了改进，在算法中引入了Markov跳变非线性系统。实验结果表明，在多目标跟踪过程中，基于Markov跳变非线性系统的粒子滤波算法，与经典粒子滤波算法相比，其抗遮挡能力大大提高，跟踪时间缩短，性能明显优于经典粒子滤波算法。

参考文献：

[1] 张海洋.基于粒子滤波的红外目标跟踪的研究[D].长沙.湖南大学,2012.

[2] 孟军英.基于粒子滤波框架目标跟踪优化算法的研究[D].秦皇岛：燕山大学,2014：25-27

[3] 丁业兵.基于Mean Shift的视频目标跟踪算法研究[D].合肥：安徽大学,2012.

[4] 孙伟.复杂背景下红外目标图像分割与跟踪研究[D].南京：东南大学,2004.

[5] 龚俊亮,何昕,魏仲慧,等.采用改进辅助粒子滤波的红外多目标跟踪[J].光学精密工程,2012,20(2):413-421

[6] LI Ji-liang,FANG Xiang-zhong,HOU Jun,et al.Mean shift based log-Gabor wavelet image coding[J].浙江大学学报A(英文版),2007,8(4):620-624.

[7] 方洋旺，伍友利，王洪强.结构随机跳变系统最优控制理论[M].国防工业出版社,2012,3：84-87

[8] 穆治亚.红外多目标实时跟踪方法的研究[D].长春：中国科学院长春光学精密机械与物理研究所，2014:38-40