渗透建模思想 培养数学创新能力

江 勇

（江苏省包场高级中学，江苏海门 226100）

引 言

在高中数学中有很多抽象的题目，想要解答这些题目就需要学生具备一定的抽象思维，但是很多抽象的题目仅仅靠学生的抽象思维是无法解答的。在这种情况下，数学建模就显得尤为重要，这也是数学建模在高中数学学习中的实际效果[1]。在高中数学教学中，培养学生抽象思维的方法主要有发散思维、融入生活、感受过程。

一、发散思维，搭建框架

在面对抽象的题目时，想要利用数学建模的思想解答首先就得进行思维发散，这样才能成功地搭建起数学建模的框架，也只有这样才能进行以后的工作，否则所有的工作都是在做无用功。

如在教学《指数函数》时，为了能够在教学中培养学生的建模意识，我在教学时特地对学生进行引导。例题：某细胞分裂时由1个分裂为2个，2个分裂为4个，3个分裂为8个，以此类推求出50个细胞分裂为多少个？这是一个典型的可以采用数学建模解答的问题。我首先让学生自己解答这一问题。在观察学生的计算过程中我发现，大多数学生都在进行烦琐的计算，还有部分学生通过化简图来解答这一问题。这两种方法都不是解答这一问题最好的方法。所以在学生都有了计算结果后，对学生进行引导。首先我让学生寻找“细胞分裂次数”与“细胞个数”两个概念之间的数量关系。学生发现细胞分裂次数与细胞数的关系如下：1 2；2 4；3 8……然后我让学生观察这些数，寻找这些数之间存在的规律。在我的引导下，学生发现这些数之间存在以下规律：细胞个数与2的细胞分裂次数相等。而根据这一规律，我们可以进行数学建模，可以假设细胞个数为y，细胞分裂次数为x，则细胞个数与分裂次数之间的关系可以用表达式y=2x来表示，这样就成功地建立了y=2x的模型，用这个模型来解答这一题目就会变得非常简单，即细胞个数y=250=1.1259×1015。这样，这一题目用数学建模的思想成功地解答出来了。

从上面的例题中可以看出，利用数学建模可以简化计算过程，如果学生不采用数学建模的思想解答该题目，仅仅依靠数学计算来解答会非常吃力。这就是数学建模思想给高中数学的学习带来的实际便利。

二、融入生活，主题探究

生活中到处都能找到数学的影子，而利用生活来学习也是一种非常不错的方法。在培养学生的数学建模思想时，教师同样可以利用生活来帮助学生养成数学建模的思维意识，这样的引导可以给学生留下深刻的印象，对学生的学习有很好的促进作用。

如在学习《空间点、直线、平面之间的位置关系》时，为了更好地帮助学生利用数学建模的方法来学习空间几何的知识，我在教学时特地利用生活中的事物来引导学生进行思考。在学习该节知识时，平面的性质公理3是这样的：“如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。用式子表示为P∈α,且P∈βα∩β=l且P∈l。”在教学时，发现学生在学习该条公理时非常吃力，所以我就用生活中的元素来引导学生通过建模来学习这一知识点。我选取的生活元素为两张能相互镶嵌在一起的硬纸，通过这一道具的演示，学生就能更为直观地感受公理3所要表述的内容。我首先将两张纸镶嵌在一起，根据公理3可以知道，要想使点P成为两个纸的公共点，则点P一定位于两张纸的交线上。而通过观察模型也发现，只有两张纸的交线作为两张纸共有的线经过了点P。所以用这样的模型来理解知识就会更为直观，也更容易。利用生活中的模型来帮助学生对相关知识进行理解时，教师一定要开阔思维，尽量寻找与所学知识相匹配的生活模型，这样才能更好地引导学生走出思维的误区，更好地认识所学知识的本质。

三、感受过程，无形传输

数学建模是一个注重过程的学习方法，所以要想使学生熟练地掌握数学建模的思想方法，只有通过日常的不断积累才能实现完全掌握的效果[2]。因此教师在日常的教学中，可以让学生感受数学建模的过程，实现在无形之中灌输数学建模的意识和思想。

如在教学《函数模型及其应用》时，我就是让学生感受建模过程实现数学建模意识的灌输和培养。由于该节课程的特点，我在教学时也是采用例题展示的方法让学生感受建模的过程，如下面的例题：如果你现在有笔钱要用于投资，有三种方案可以选择，三种方案的回报分别如下：方案①，每天回报40元；方案②，第一天回报10元，以后每天比前一天多回报10元；方案③，每天回报0.4元，以后每天的回报比前一天翻一番，投资哪种方案回报最大？

在建模之前，我首先对问题进行分析，问题中求得最大回报应该是累计回报。所以为了求出累计回报最大的情况，我们先假设第x天所得的回报为y元，则三种方案的函数模型分别为：方案① y =40（x∈N*）；方案②y =10x（x∈N*）；方案③y =0.4×2x-1（x∈N*），之后根据这三个函数分别绘制出对应的图像，再根据题目意思绘制出累计回报效益，这样就能直接从图上读出选择哪种方案获得的收益最大。在整个解题过程中，我没有让学生参与，只是让他们观察感受，这样能让学生更好地体会到数学建模的过程。

四、借助范例，举一反三

通过前面三个环节的建模思想的学习，接下来这一环节就是学生利用建模思想进行练习的环节。在该环节教学时，教师可以借助范例，引导学生正确有效地找到思考方向，让学生在独立练习时能够熟练地运用建模思想。

如在教学《三角函数恒等变换》时，为了更好地引导学生利用建模思想来解决实际问题，我就利用范例来引导学生在解答问题时采用建模思想。范例试题如下：如图1所示，在海岛D上有一座海拔1km高的山，山顶上有一个观察站A，上午11时测得一轮船在岛的北偏东60°的C处，俯角为30°；11时10分又测得该船在岛的北偏西60°的B处，俯角为60°，求该船的行驶速度为多少？

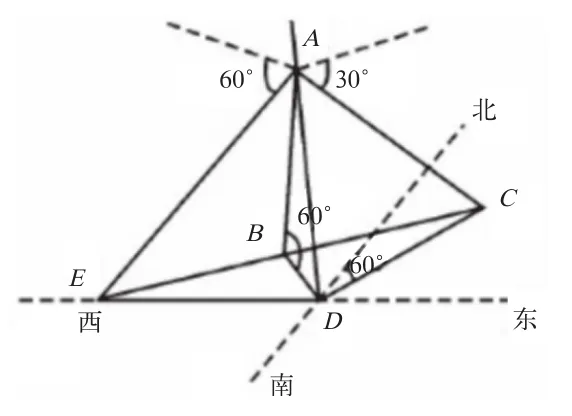
图1

该题目是将三角函数的知识运用于实际问题的典型例题，在解答时也需要通过构建三角形来解答，用这样的例题来引导学生利用建模思想可以取得比较好的效果。解答过程如下：

这一题目的解答思路首先是利用题目已知条件构建三角形，然后在构建的三角形内套用余弦定理求出未知量。

教师在该环节教学时，一定要选取一些有代表性的试题，这样才能更好地引导学生运用建模思想，更好地培养学生运用建模解答问题的意识，能够真正有效地帮助学生提升数学思考能力，将高中数学的教学质量提升到一个新台阶。

结 语

综上所述，在高中数学教学中培养学生数学建模意识的方法有很多，种类也很多，教师在进行教学时一定要根据实际情况选择合适的方法，这样才能取得最好的教学效果，也能最快地使学生的能力成长起来。

[1]何松.数学建模思想在高中数学中的运用探析[J].数学学习与研究，2016，(13)：137.

[2]朱斌.中学生数学建模活动的几点探讨[J].中学数学杂志，2014，(11)：28-30.