数形结合解题法常见错误类型剖析
罗永辉
(广东省佛山市南海九江中学 528000)
数形结合是很重要的数学思想,由于利用了抽象的数与具体的形之间一一对应的关系,从而使推算及判断过程大大简化,简明快捷,十分有效.但是由于判断和推理依赖的是图形的直观性,且图形又具局限性,其严密性差等特点,还有数形之间并不等价,因此常引起判断失误,产生错解,影响教学效果.下面剖析几类常见的错误,以期引起重视.
一、因作图缺准而产生的错误
借助图形解题,不但要尽量准确地描绘出曲线的图形,还要注意同一坐标系中不同图象的相对位置.
例1 判断方程lnx-x+1=0的实根个数.
错解将原方程转化为lnx=x-1,令f(x)=lnx,g(x)=x-1,在同一直角坐标系中作出图象,如图1.可以很容易判断出有两个实根.

图1 图2
剖析其实g(x)=x-1刚好与f(x)=lnx相切,切点为(1,0).正确图象如图2所示.故有一个实根.
二、忽略图形的存在性而造成的错误
有时当问题的结论不太明朗时,凭主观臆测,结果会使问题无中生有,会使错误的结论变得顺理成章.
例2 如果抛物线y2=6x与圆(x-a)2+y2=4没有公共点,求实数a的取值范围.
错解如图3.圆心在圆与抛物线内切与外切圆圆心之间时都有交点,反之无公共点,显然a= -2时外切,再把抛物线代入圆方程消去y得:
x2+(6-2a)x+a2-4=0.
(*)


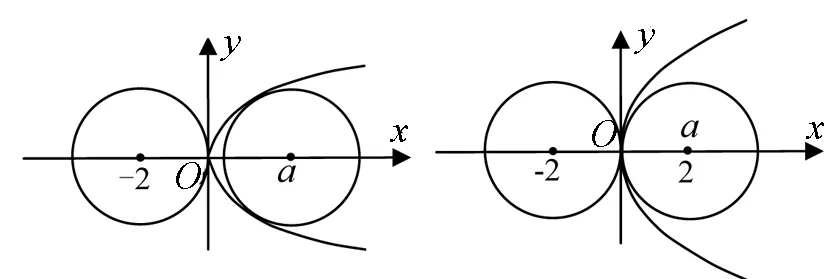
图3 图4
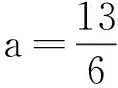
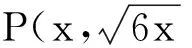


所以a的取值范围是a<-2或a>2.
三、忽略图形的整体性而造成的失误
在同一坐标系中作出几个函数的图象来比较时,我们一定要注意函数图象的延伸趋势以及伸展“速度”.因为我们画出的只是函数图象的一小部分,而不是全部.
例3 方程2x-x100=0的解的个数是 ( )
A.0个 B.1个 C.2个 D.3个
剖析正确的答案是D.但多数的学生却选了C.其方法是把方程转化为两曲线y=2x与y=x100交点的个数即是解的个数,方法和思路是对的.但他们却作了如图5的图象,并据此选了C.但这个图象只是局部而并非整体,在x充分大时,两曲线还有一个交点.但这个交点离原点太远了,我们很难作出.
我们可从y=2x与y=x2的交点来帮助理解例3的另一交点(如图6).
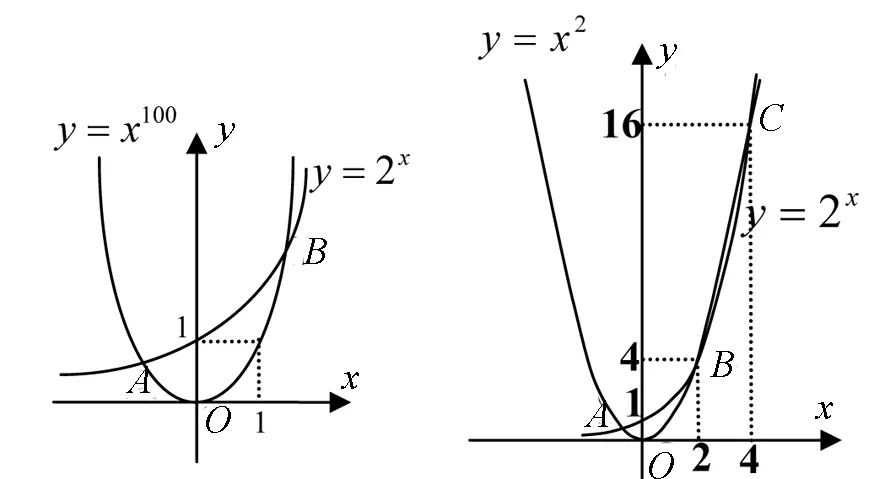
图5 图6
数形结合解题,虽然有这样或那样的失误,但仍不失为一种解题的好方法.不过如华罗庚所说的: “数缺形时少直观,形缺数时难入微.” 所以只有认真分析,精确作图,并配以严密的推理与验证,才能使数与形互相补充,起到既提高解题速度,又保证解题质量的效果.
参考文献:
[1]赵久勇.数型结合应用中的错误剖析 [J].高中数学教与学,2011(6): 12-15.
[2]童其林.用数型结合思想方法解题时的常见错误分析 [J].广东教育(高中),2014(1): 24-27
[3]刘桦.谈运用数型结合法解题的误区 [J].中学数学,1995(9): 41-43

