高考数学两道几何题的解析与启示
孙丽萍
(陕西省洛南中学 726100)
基金项目:陕西省第四批中小学幼儿园学科带头人培养对象专项研究课题《基于混合学习模式的立体几何教学研究》阶段成果(课题立项号:XDKT4042).
立体几何中的夹角计算以及向量数量积的应用是近几年高考的常见考点,而涉及到这两类知识点的问题解决方法一般也不唯一,可以一题多解.以下通过2017年全国高考课标Ⅱ卷理科数学试题中的两道选择题,从不同角度展示它们的常见解法.
一、真题解析
题目1 (2017年高考课标Ⅱ卷理数)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )

图1
分析1 传统异面直线定义法.如图1(具体做法:通过平移异面直线即作它们的平行线,找出异面直线所成角,再以此角为其一内角构造三角形,通过解三角形求得结果.)
解取BB1的中点O,过O作OE∥AB1交AB于点E,作OF∥BC1交B1C1于点F.
记异面直线AB1与BC1所成角为θ,则θ=∠EOF或θ=π-∠EOF.
连结EF,取A1B1中点G,连结GE,GF.

因为在△A1B1C1中,由余弦定理得



所以在△EOF中,由余弦定理得

分析2 空间向量建立坐标系法.如图2(具体做法:建立合适的空间直角坐标系,求出关键点的坐标,进而求出所需向量坐标,再由公式关系求出所要结果.)
解以B为空间原点,过点B与BC垂直的直线为x轴,BC所在直线为y轴,BB1所在直线为z轴建立空间直角坐标系.
如图2所示,则B(0,0,0),C1(0,1,1),B1(0,0,1).

图2 图3
分析3 空间向量基本定理法.如图3(具体做法:在几何体的边棱线中选三个不共线的向量作为基底,把两异面直线的方向向量分别用基底向量表示出来,再用数量积的性质求解.



分析1 数形结合推理法.如图4.(具体做法:数形结合根据向量加法平行四边形法则,化简向量式,确定取最小值时P点位置,结合均值不等式求解)







图4 图5
分析2 解析法.如图5所示.(具体做法:建立合适的平面直角坐标系,将向量及其数量积用坐标表示,再结合二次式配方求得)
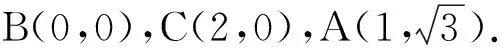


二、解法启示
以上尽管只是两道选择题,但都具有一定的典型代表性,较好地考查了学生的图形分析、空间想象、逻辑推理、知识迁移、基础知识综合应用等各方面能力,其中题目1立体几何涉及的知识点,近年来不仅在选择题目中考察,而且也是解答题的必考考点,只是一般会增加设问的内容.自从引入空间向量作为工具解决立体几何问题,其呈现的特点为:方法统一、程式规范,偏重代数化的计算,可操作性强,弱化了解题技巧,降低了思维难度,多数同学对其甚是青睐,淡化和忽视了对传统和其他方法的考虑.而在有的问题中运用传统方法会更简洁方便,例如2017年全国高考课标Ⅱ卷理科数学第19题的第一问.
题目2的两种方法各有思维考虑的侧重点,方法1更注重对概念定理的理解和应用,知识点的交叉和跨度以及综合性较强;而方法2主要体现了数学上常用的转化思想,即实现化几何为代数的方法,降低了思考难度.
参考文献:
[1]韩军利,程妍.高中数学中的一题多解问题[J].数学学习与研究,2014(03):77.
[2]薛孝乐.一道解析几何题的多种解法[J].数学通报,2006(04):20-21.

