高考试题中的空间线线角
苏艺伟
(福建省龙海第一中学新校区 363100)
立体几何是高中数学主干知识,它紧紧围绕数量关系,空间形式,数形结合,公理化思想这4条主线,让学生有机会体会和认识一些数学本源性问题.其中的空间角是高考重点考查的内容,包括线线角,线面角,面面角.求解空间角一般可以采用综合法和向量法(包括向量基底法和向量坐标法).本文以求解空间中的线线角为例进行说明.
求解空间中的线线角一般可以采用以下方法.
方法1:综合法
立体几何问题解决的基本策略是立体问题平面化.综合法以公理,定理体系为理论基础,对空间中的点,线,面的关系从形上去认识,根据判定定理与性质定理把空间的线线,线面,面面关系通过传递转化为平面内的线线关系,具有逐步过渡,步步为营,推理严谨,简洁明了等特点.而借助辅助线的定位过渡是解题的难点与关键,需要学生构建整体观念和具有一定的平面几何基础.
方法2:向量法
向量法的实质是几何问题代数化(将几何问题转化为数量问题进行量化处理),把立体几何从形向数上延伸,用代数运算的方式解决立体几何问题,运算公式植根于综合法,具有跨越定位过程,隔空传递,关注结果,化繁为简,操作容易等特点.
例1 (2017年全国Ⅱ卷)
已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
方法1:综合法

图1 图2
如图1所示,取AB中点M,BC中点Q,B1B中点N,B1C1中点P,连结MQ,PQ,MP,MN,PN.由于AB1∥MN,BC1∥PN,所以异面直线AB1与BC1所成的角即为∠MNP或其补角.


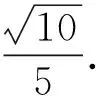
方法2:基底法

设异面直线AB1与BC1所成的角为θ,则cosθ=
方法3:坐标法

图3



设异面直线AB1与BC1所成的角为θ,则cosθ=
例2 (2015年浙江卷)
在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成角的余弦值是________.

图4 图5
方法1:综合法
如图4所示,连结DN,取DN中点E,连结ME,CE.
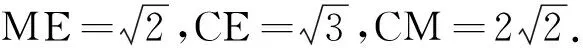


方法2:基底法
如图5所示,

|c|=3.



设异面直线AN与CM所成的角为θ,则cosθ=
方法3:坐标法

图6


设异面直线AN与CM所成的角为cosθ=
上述两种方法是处理空间中两直线所成角的常用方法.方法1为综合法,理论依据是立几中的三个公理以及相关定理,性质.其关键在于作出辅助线,进而证实与解答.方法2是基底法,理论依据是空间向量基本定理(空间中任意一个向量都可以表示成不共面的三个向量的线性组合),需要三个模与相互夹角已知的不共面向量作为基底,用其表示空间内任意向量,通过数量积等运算实现化归.方法3是建立空间直角坐标系,将几何元素以坐标的形式体现出来,转化为坐标的运算.三种方法都具有各自的优点,不可偏废.在实际解题中我们应该要灵活根据题目条件选择合适的方法以期达到最优化效果.
例3 (2014年新课标全国卷Ⅱ)
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1中点,BC=CA=CC1,则BM与AM所成角的余弦值为( )


图7
解析如图7所示,以C为原点建立空间直角坐标系.
设BC=CA=CC1=2,则A(0,2,0),N(0,1,2),B(-2,0,0),M(-1,1,2),
设异面直线BM与AN所成的角为θ,则cosθ=
例4 (2014年大纲卷第11题)

图8
已知二面角为α-l-β为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135° ,则异面直线AB与CD所成角的余弦值为 ( )


其中结论正确的是________.

例5 (2017年全国Ⅲ卷)
设a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴,有以下结论:
(1)当直线AB与α成60°角时,AB与b成30°角.
(2)当直线AB与a成60°角时,AB与b成60°角.
(3)直线AB与a所成角的最小值为45°.
(4)直线AB与a所成角的最大值为60°.
其中结论正确的是____.

图9
解析如图9所示,设直线a为直线NC,直线b为直线MC,设直线AB与a所成的角为α,直线AB与b所成的角为β.
作BM∥C,BN∥MC,则α=∠ABM,β=∠ABN.

因此有cosα=cos∠ABC·cos∠CBM,
(1)
cosβ=cos∠ABC·cos∠CBN=cos∠ABC·sin∠CBM.
(2)


所以当直线AB与α成60°角时,AB与b成60°角.第(2)个正确.
又因为斜线与射影所成的角是该斜线与平面内任意 一条直线所成角中最小的,故直线AB与a所成角的最小值为45°.第(3)个正确.
评析上述三道试题从图形特征以及待求目标来看,采用向量法显然不合适,因此采用综合法进行求解.
空间中的线线角折射出学生对综合法与向量法的理解,在实际教学中,要正确处理好综合法与向量法的运用关系,不能顾此失彼.笔者认为,在高三一轮复习时,要强调使用几何法,以巩固定理,规范证明过程书写,提高推理论证能力.在高三二轮复习时,要让学生根据实际,灵活选择以实现简化解题过程之目的.
参考文献:
[1]李波.2017年高考立体几何专题解题分析[J].中国数学教育,2017(7-8):113-117.

