挖掘习题资源 优化课程资源

☉江苏省丹阳市第五中学 林伟民

蕴含着数学知识的例题、习题是学生掌握数学基本知识、方法、思想、技能的主要资源，训练强化是传统教学中达成知识的掌握与能力的提升，但是，仅仅利用训练是无法使学生胜任富含智慧与挑战性的数学学习的.近年来的很多高考试题都尤其侧重于例题、习题的再加工与创造，因此，教师应不断更新教学观、教材观并将教材中的习题教学资源充分挖掘出来以实现课程资源的不断创造.

一、挖掘重要结论

挖掘习题或复习参考题在解题中的作用能够使学生更加深刻地认识到数学知识、定理等的本质与价值，因此，教师应在深入研究教材意图的基础上逐步提炼典型例题或习题的思维方法并为学生学习与解题作出示范与指导.

比如，在抛物线y2=2px（p＞0）的焦点F作一直线与抛物线相交于P（x1，y1），Q（x2，y2）两点这一问题中，就可以挖掘出y1y2=-p2（*）这一结论，教师可以引导学生体会这一结论在解题中的作用以补充课程资源.

例1 过抛物线y2=2px（p＞0）的焦点F的直线与抛物线相交于P（x1，y1），Q（x2，y2）两点.求证

二、挖掘思想方法

教师在教学中应时刻注意教学过程中教与学的双向性并将数学知识与思想方法融于整个教学过程中，这对学生数学能力的培养、数学思维品质的提高、例题教学效率的提升来说都是极其有利的.例如，下述函数奇偶性的习题教学中就可以着眼于思想方法的挖掘以创

三、改进条件结论

造课程资源.

例2已知偶函数（fx）在（0，+∞）上为增函数，（fx）在（-∞，0）上是增函数还是减函数呢？请证明你的结论.

师：结合偶函数的图像特征与本题实际请判断（fx）在（-∞，0）上的单调性.

生：函数（fx）在（-∞，0）上为减函数.

师：要想证明你的结论，应着眼于哪个内容的证明呢？

生：证明当x1＜x2＜0时，（fx1）＞（fx2）.

师：假如已知函数的单调递增区间为（0，+∞），我们应该怎么把未知区间上的x1＜x2＜0转化至已知的单调递增区间（0，+∞）上呢？

生：因为x1＜x2＜0，因此只要乘-1，得-x1＞-x2＞0.

师：题中（fx）在（0，+∞）上为增函数这一条件告诉了我们什么？

生：（f-x1）＞（f-x2）.

师：我们可以借助什么条件来建立（f-x1）与（fx1）、（f-x2）与（fx2）的关系呢？（f-x1）与（fx1）、（f-x2）与（fx2）之间的关系又是怎样的？

生：根据题中已知的（fx）为偶函数这一条件可知，（f-x1）=（fx1），（f-x2）=（fx2）.

教师与学生在问答之间不断完善解题过程，数形结合这一思想方法与分析法这一解题方法在解题中得到了很好的运用、领会与理解.学生在数学思维得到锻炼的同时也提升了自己分析与解决问题的能力.

对教材习题的条件和结论之间的关系进行深入的研究能够挖掘出一系列的问题，处于这一系列问题核心的教材习题不仅能够揭示问题的本质，同时还能给学生创造更多横向、纵向的思考空间.

以（*）为例，假如直线不是经过焦点却是x轴上的某一定点，结论又会产生怎样的变化呢？如果命题的条件与结论对换之后命题还会成立吗？

例3 过x轴上一定点（m，0）作直线与抛物线y2=2px（p＞0）相交于A，B两点，若A（x1，y1），B（x2，y2），则y1y2是不是定值呢？

例4 直线l与抛物线y2=2px（p＞0）相交于A，B两点，若A（x1，y1），B（x2，y2），则y1y2=-p2，直线l是否会经过某一定点呢？若x1x2=p2又会怎样？

这两个问题并不难，但教师在教学中应将自己的教学重心从片面注重知识传授转变为学生学习能力的培养上，不仅如此，教师还应在关注学生学习结果与过程中引导学生学会观察、思考、表述以及动手操作，使学生在学会自己归纳、分析问题的过程中学会自主学习，在亲身经历、感受、理解知识的产生与发展中锻炼自己的数学素养与创新思维能力.

四、探究一般结论

教师在教学时如果能够在教材的运用上不时调适取向并对教材习题的功效进行有效的挖掘，结合不断创生取向的教学方式必然能够开发出更多可以利用的数学课程资源，这些课程资源的合理应用能够很好地培养学生的思维能力与数学综合素养.

例5 已知等比数列{an}的前n项和为Sn，S3，S9，S6成等差数列，求证：a2，a8，a6成等差数列.

教师和学生根据这一题目是否能够推广并最终得到一个一般性的结论呢？教科书习题的使用价值会因为这一问题的推广得到更大的提升，因此，教师应将单纯的作业订正课进行一定的改进，使得学生能够全身心地投入到探究性学习的活动课中来.

师：大家觉得推广这一结论可以从哪些方面切入呢？

生1：将3，6，9改成k，2k，3k来试试看呢？

生2：或者改成k，k2，k3试试看呢？

师：大家觉得这样变化可以吗？等会儿我们可以进行检验.

师：如果按照大家的想法，那将2，5，8改成什么呢？

生1：我觉得可以改成k-1，2k-1，3k-1.

生2：或者将其对应写成k-1，k2-1，k3-1.

师：我们的猜想对不对呢？我们应该怎样检验这些猜想呢？

生：可以运用证明来解决.

师：大家有没有考虑过这些命题的反面是否成立呢？

生：证明它们的逆命题也是可以的.

接着，教师可以引导学生对自己的猜想付诸实践中探索、整理并达成检验的目的，经过师生的共同研究发现生1的做法是可行的，生2的猜想是不能成立的，整理结果如下：

变式1：设Sn为等比数列{an}的前n项和，k∈N，k≥2，如果Sk，S3k，S2k成等差数列，那么ak-1，a3k-1，a2k-1成等差数列.

证明：将等比数列{an}的公比记作q，易知q≠1.

因为Sk，S3k，S2k成等差数列，

所以ak-1+a2k-1=2a3k-1，所以ak-1，a3k-1，a2k-1成等差数列.

令人感觉有趣的还有：

变式2：设Sn为等比数列{an}的前n项和，其公比q≠1，k∈N+，k≥2，且ak-1，a3k-1，a2k-1成等差数列，那么Sk，S3k，S2k也成等差数列.

证明：由ak-1，a3k-1，a2k-1成等差数列可知，

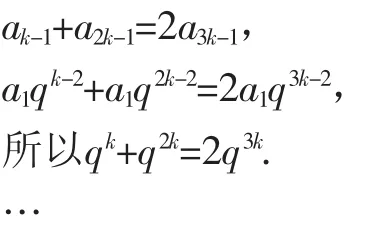
所以Sk、S3k、S2k成等差数列.

教师接着再引导学生从命题1与命题2的探讨中归纳出这方面的定理，习题探究的功效也在这一过程中得到了完美的体现.

五、深化问题研究

学生解题能力的锻炼必须要有一定的练习作为支撑，不过，仅凭练习但不关注内涵很有可能适得其反.比如说，抛物线的焦点弦的一些问题链中所包含的思想方法一样可以推广至其他圆锥曲线的解题中，因此，教师在教学中应加强多题一解或一题多解的研究使问题变得更加深入，课程资源得到深化、整合的同时也使学生的知识结构得以网络化.

总之，教材中这些蕴含数学知识的例题、习题同时也隐藏着学生应该掌握的基本思想、方法与技能，传统教学中的强化训练往往会把学生锻炼成机械解题的操作工，这与新课程对教师的教与学生的学所提出的要求都是极不相符的，因此，教师一定要把教材中隐含的资源挖掘出来并将其设计成供学生挑战的练习，立足教材但又优于教材、超越教材的设计与创新使学生能够在知识原型上得到思维的深入与拓展，学生在富有思想性的数学知识产生的过程中探索、交流并不断提升自己的思维能力，课程资料的挖掘与整合也使学生良好的数学素养与品质得以形成和发展.H