求解不定信赖域子问题的分段三次Hermite插值法

李琳俊，王希云

(太原科技大学应用科学学院，太原 030024)

作为一种重要的数值方法，信赖域算法以其全局收敛性及较强的适定性，一直以来受到最优化研究者们的广泛关注。

运用信赖域算法求解，每一次从点开始迭代时，对于如下信赖域子问题,均需分别求解。

(1)

在(1)中，符号的意义为：B∈Rn×n是目标函数在点x(k)x(k)对应的Hessian矩阵或者其近似形式，g∈Rn是目标函数在点x(k)对应的梯度,δ∈Rn是待求的变量，Δ∈R是信赖域的半径。假定该算法在点(μk,f(μk)),(k=0,1,…m).进行迭代，伴随着Δ不断变化，(1)的解δ*也发生相应变化，将各个变化过程形成的点连线可确定一条空间曲线,叫做最优曲线[1]。

由精确求解信赖域子问题方法的思想，易知最优曲线的参数方程为：

δ=-(B+μI)-1g,(μ≥0)

(2)

从而可构造如下形式的微分方程模型[2]:

再用分段三次Hermite插值法[3]求解此模型。

在(2)前提下，引入新的函数：

y=f(μ)=‖δ‖2=‖-(B+μI)-1g‖2,(μ≥0),那么(1)的解δ*如下：

当μ=0,δ*=-B-1g;

当μ>0，解的确定依赖于求解以下形式的一元非线性方程：

f(μ)-Δ=‖-(B+μI)-1g‖2-Δ=0.

解该方程可确定μ*，则最优解：

δ*=-(B+μ*I)-1g.

子问题(1) 在B不定情况下，不一定会有极小值点。甚至可能会没有平稳点[4]。一般而言，可用强迫矩阵正定的方法修正B来避免这种情况。近年以来，求解不定信赖域子问题的方法有：修正分段割线法[5]，混合折线法[6]双割线折线法[7]等。本文中，通过修改Cholesky分解修正不定矩阵B，进而构造新的对称正定矩阵G[2].修正不定矩阵之后，问题已经转化为求解正定形式的信赖域子问题。再依据分段三次Hermite插值法[3]，提出修正分段三次Hermite插值法来解(1).

1 分段三次Hermite插值法的思想

分段三次Hermite法是依据求解(1)的分段割线法，对以下的节点：

(μk,f(μk)),(k=0,1,…m).

运用三次Hermite插值法来构造m条曲线，

Hk(μ),(k=0,1,…m)为曲线方程。将m条曲线连接起来，就是分段三次Hermite曲线。在最后的两个插值点：(μm-1,f(μm-1)),(μm,f(μm))构造三次Hermite插值函数H(μ)近似代替f(μ)，再求方程：f(μ)-Δ=0的解μ*，进一步确定信赖域子问题的最优解：

δ*=-(B+μ*I)-1g,(μ≥0).

此算法优于修正分段割线法之处：用分段三次Hermite插值法确定的曲线，可以避免用修正分段割线法构造的曲线在节点处出现尖点，从而能更好的逼近最优曲线。

2 修正不定矩阵

在文献[4]中，修改Cholesky分解可以修正不定矩阵B，进一步将不定问题转化为正定问题。

3 算法框架

Step0 给定梯度g，不定矩阵B,信赖域半径Δ，步长h.令n:=0.

Step1用修改Cholesky分解修正B，得新正定矩阵G,且令：B=G.

Step2当μ0=0，求f(μ0)与f′(μ0).若：f(μ0)≤Δ，取：δ*=-B-1g，停止计算。否则使k:=1，转step 3.

Step3计算f(μk)和f′(μk)，μk=μk-1+h.在插值节点(μk-1,f(μk-1))和(μk,f(μk))间，应用三次Hermite插值法确定曲线Hk(μ),将所有的小区间结合起来，形成分段曲线Γ.

Step4若f(μk)≤Δ，则μ*处在曲线Hk(μ)上，求解方程：Hk(μ*)=Δ确定μ*，最优解为：δ*=-(B+μ*I)-1g,停止计算。否则，使k:=k+1,转step3.

注1：在step 0，步长h越小，由以上算法求得的(1)之解δ*越准确。

注2：在step 3，分段曲线Γ形式如下：

其中：

(k=1,2,…m).

4 数值实验及结果分析

基于本文提出的修正分段三次Hermite插值法，对于测试函数Function 1和Function 2(见附录)，选取不同的信赖域半径Δ，分别用算法4与修正分段割线法来计算最优解，并与精确解进行比较。CHDH为修正的分段三次Hermite插值法(即算法4)，CHDF为修正分段割线算法，HD为混合折线法。具体结果见表1和表2.

表1 测试函数1的数值结果
Tab.1 Numerical results of Function 1

ΔCHDH(Hermite)CHDF(分段割线)精确解Function11-14．177285-14．3490051-14．1772732-28．5609402-29．4507523-28．5604233．5-50．9305577-54．5986931-50．9140114-58．6560535-63．8000136-58．6453835-74．6836005-83．4756002-74．6108835．28-79．2372724-89．3518536-79．2104076-91．7245303-89．4577778-91．3140317-110．6027419-89．4577778-108．816228-128．8753917-89．4577778-127．162279-147．2780263-89．4577778-146．385179．1-149．1596098-89．4577778-148．356699．2-151．0517361-89．4577778-150．3372610-166．6505065-89．4577778-166．5095312-211．0244466-89．4577778-209．5328114-267．7873558-89．4577778-256．3357416-267．7873558-89．4577778-306．9823818-267．7873558-89．4577778-361．5142919-267．7873558-89．4577778-390．2463521-267．7873558-89．4577778-450．6559922-267．7873558-89．4577778-482．3376822．4-267．7873558-89．4577778-495．2865822．5-267．7873558-89．4577778-498．54849

表2 测试函数2的数值结果
Tab.2 Numerical results of Function 2

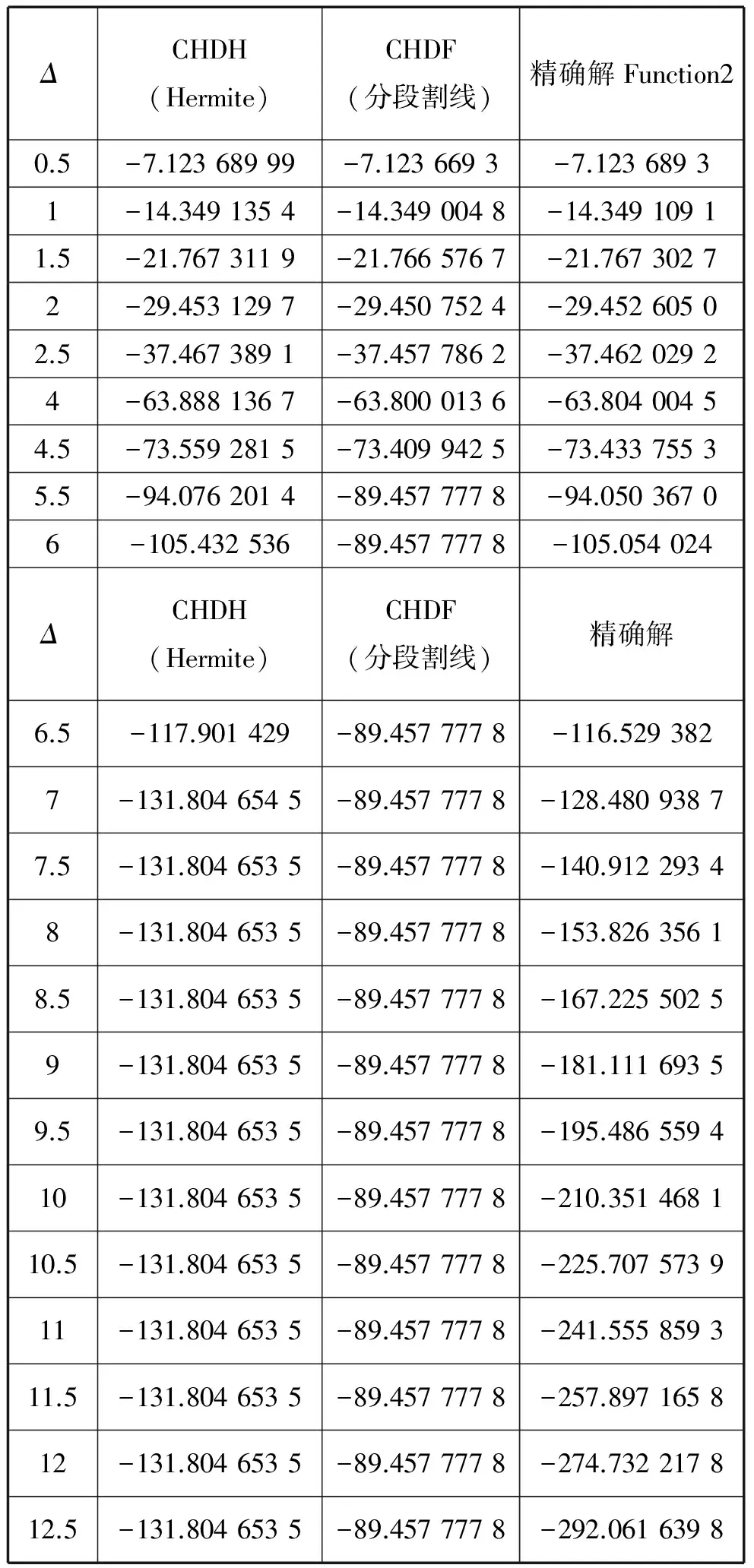
ΔCHDH(Hermite)CHDF(分段割线)精确解Function20．5-7．12368999-7．1236693-7．12368931-14．3491354-14．3490048-14．34910911．5-21．7673119-21．7665767-21．76730272-29．4531297-29．4507524-29．45260502．5-37．4673891-37．4577862-37．46202924-63．8881367-63．8000136-63．80400454．5-73．5592815-73．4099425-73．43375535．5-94．0762014-89．4577778-94．05036706-105．432536-89．4577778-105．054024ΔCHDH(Hermite)CHDF(分段割线)精确解6．5-117．901429-89．4577778-116．5293827-131．8046545-89．4577778-128．48093877．5-131．8046535-89．4577778-140．91229348-131．8046535-89．4577778-153．82635618．5-131．8046535-89．4577778-167．22550259-131．8046535-89．4577778-181．11169359．5-131．8046535-89．4577778-195．486559410-131．8046535-89．4577778-210．351468110．5-131．8046535-89．4577778-225．707573911-131．8046535-89．4577778-241．555859311．5-131．8046535-89．4577778-257．897165812-131．8046535-89．4577778-274．732217812．5-131．8046535-89．4577778-292．0616398

同理，对于不同的Δ，分别用算法4与混合折线法求解测试函数1和2，qHD-qCHDH表示的是：对于确定的测试函数以及信赖域半径，采用混合折线法得到的最优解与采用算法4得到的最优解之差，该差值越大说明算法4越好。具体结果见表3和表4.

第一个测试函数Function 1的拟牛顿步为：

‖Gg‖2=22.398,

第二个测试函数Function 2的拟牛顿步为：

‖Gg‖2=11.47.

数值实验：

表3 测试函数1的数值结果
Tab.3 Numerical results of Function 1

ΔqHD-qCHDHCHDH(Hermite)HD(混合折线)Function110．035149834-14．17728546-14．1421356220．276668954-28．5609402-28．284271253．51．433083012-50．9305577-49．4974746842．087511041-58．65605354-56．5685424953．972922454-74．68360057-70．710678125．284．566796383-79．23727248-74．6704760966．871716555-91．7245303-84．85281374711．60779257-110．6027419-98．99494937815．73830672-128．8753917-113．137085919．99880567-147．2780263-127．27922069．120．46617565-149．1596098-128．69343429．220．94408835-151．0517361-130．107647710256．7824772-166．650506590．1319707812315．9009656-211．0244466104．87651914385．5490951-267．7873558117．761739316396．6248606-267．7873558128．837504818405．9183677-267．7873558138．131011922-183．4633192-267．7873558-451．25067522．4-183．4633192-267．7873558-451．25067522．5-183．4633192-267．7873558-451．250675

从表1与表2，易知：CHDH(Hermite)比CHDF(分段割线)更接近精确解，且CHDF(分段割线)在Δ为很小的半径(Function 1中，Δ=5.28；Function 2中，Δ=5.5)便陷入局部最优，而CHDH(Hermite)在整个求解过程较为稳定。

从表3与表4，易知：CHDH(Hermite)所得最优解明显优于HD (混合折线法) 。

综上所述，修正分段三次Hermite插值法求解信赖域子问题有效可行，从而拓宽了对于不定信赖域子问题求解的研究。

表4 测试函数2的数值结果
Tab.4 Numerical results of Function 2

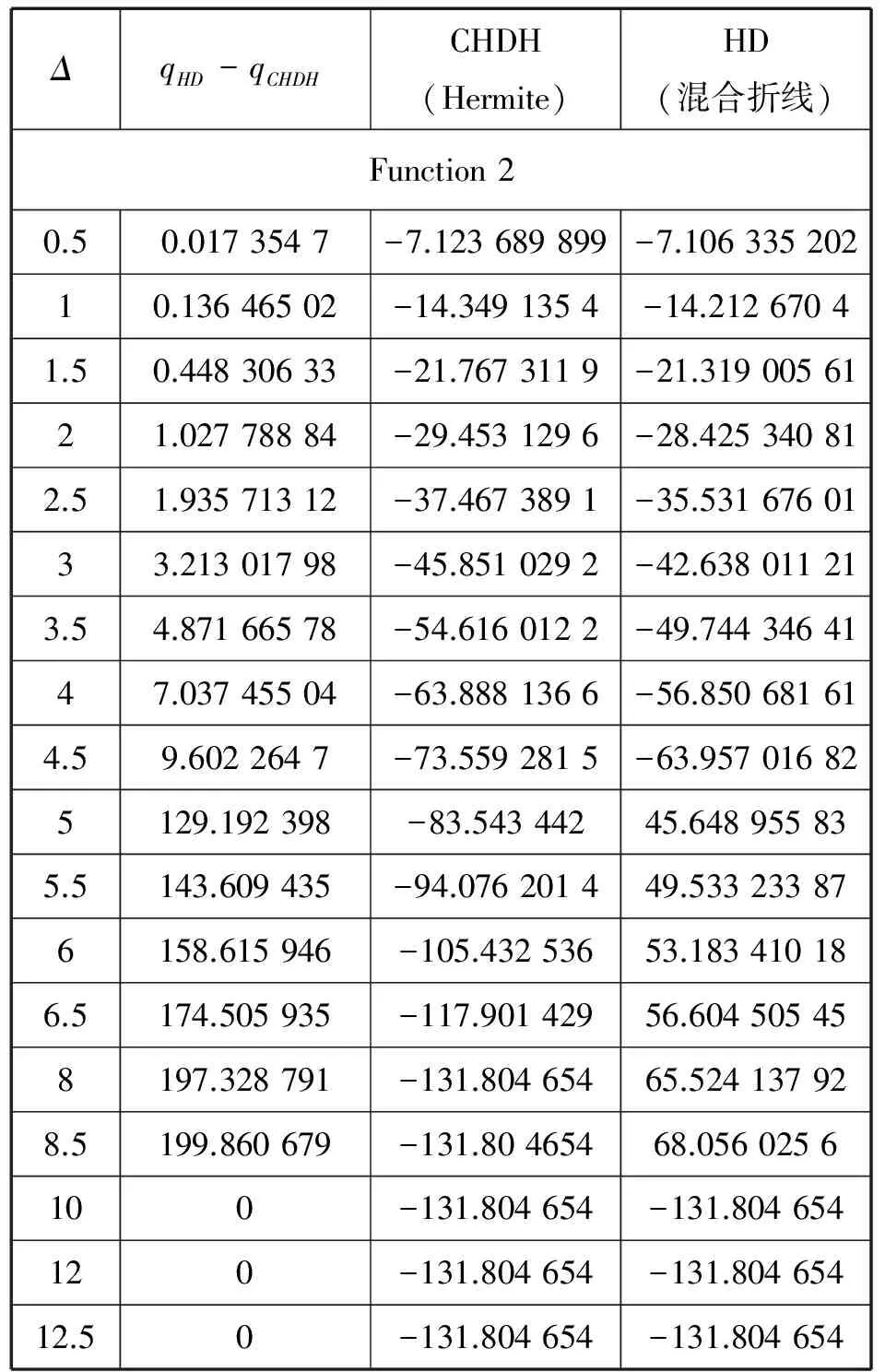
ΔqHD-qCHDHCHDH(Hermite)HD(混合折线)Function20．50．0173547-7．123689899-7．10633520210．13646502-14．3491354-14．21267041．50．44830633-21．7673119-21．3190056121．02778884-29．4531296-28．425340812．51．93571312-37．4673891-35．5316760133．21301798-45．8510292-42．638011213．54．87166578-54．6160122-49．7443464147．03745504-63．8881366-56．850681614．59．6022647-73．5592815-63．957016825129．192398-83．54344245．648955835．5143．609435-94．076201449．533233876158．615946-105．43253653．183410186．5174．505935-117．90142956．604505458197．328791-131．80465465．524137928．5199．860679-131．80465468．0560256100-131．804654-131．804654120-131．804654-131．80465412．50-131．804654-131．804654

附录：测试函数

Function 1:

s.t.‖δ‖2≤Δ.

Function2:

s.t.‖δ‖2≤Δ.

参考文献：

[1] 徐成贤，陈志平，李乃成.近代优化方法[M].北京：科学出版社，2002.

[2] 李亮，王希云，张雅琦，等.一种求解二次模型信赖域子问题的休恩算法[J].太原科技大学学报，2014,35(2)：151-155.

[3] 于海波，王希云，李亮.解信赖域子问题的分段Hermite插值法[J].太原科技大学学报，2014,35(3):226-230.

[4] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2010.

[5] 于海波，王希云，李亮.一种求解不定信赖域子问题的精确解法[J].太原科技大学学报，2015,35(2):156-160.

[6] 赵丹.解信赖域子问题的混合折线法[J].徐州师范大学学报：自然科学版,2009,27(3) :38-41.

[7] 邵安，王希云.一种求解不定信赖域子问题的双割线折线法[J].太原科技大学学报，2011,32(6):483-487.

[8] 杨蕊.矩阵的Cholesky分解的Matlab实现[J].中国科技信息：基础及前沿研究，2007(4)：273-274.