InSAR形变场最佳插值算法对比研究

李 岩，韩 蕾

(1.中国地震局第二监测中心，陕西西安 710054；2.西安欧亚学院人居环境学院，陕西西安 710065)

1 引 言

合成孔径雷达干涉测量(InSAR)因具备全天时、全天候、大范围监测，有一定穿透能力等优势，已广泛应用于地震同震形变等地壳运动领域[1-2]。通过对形变前后SAR影像进行干涉处理，提取地形和地表形变信息，可以实现地表运动的有效监测[3-4]。

在应用过程中，由于卫星原始影像畸变、处理参数设置不当、地形地貌复杂等因素造成干涉图像相干性差异很大，导致形变信息不全，影响后续分析及反演结果的精度。

为了解决上述问题，多种图像插值算法被引进到InSAR处理过程以提高形变场质量，但不同的插值算法会导致获取的最终形变信息不一致。针对这一问题，本文选取了4种常用的图像插值算法，并通过真实震例对比分析了各算法优缺点，为准确获取插值形变场提供技术参考。

2 常用插值算法

InSAR形变场的精度和保真度是进行地震同震破裂和应力变化反演的重要保障。由于InSAR形变场像元的物理属性，以及图像插值算法理论模型的不同，使得最终插值结果与实际形变存在差异。当前常用的插值算法包括最邻近插值、双线性插值、立方卷积插值和正弦函数插值[5-7]。

2.1 最邻近插值法

最邻近插值法又称零阶插值，该方法通过反向变换，选取计算像元周围4个原始像元中距离最近的一个原始像元的灰度值作为新值点。此算法简单且直观，但是当图像中包含像元之间灰度级的细微结构变化时，应用最邻近插值法难以保证结果的精度。

2.2 双线性插值法

双线性插值法又称一阶插值，其核心思想是在两个方向分别进行一次线性插值，计算像元的灰度值，根据两个方向上各两个最邻近像元的灰度值加权平均计算得到。因此该算法比最邻近插值法计算量大，精度明显提高，不会出现像元值不连续的情况。但是双线性插值法具有低通滤波器的性质，会使得高频分量受损，导致对比度明显的分界线在一定程度上变得模糊。

2.3 立方卷积插值法

立方卷积插值法能够克服上述两种算法的不足，其主要思想是取计算像元点周围的16个原始像元点作为参考值，在水平方向、垂直方向上分别进行三阶插值，最后计算得到计算像元的灰度值。由于考虑了计算像元点周围更多原始像元点的相关性，因此计算得到的像元灰度值也会更接近真实值，可以比双线性插值法更加清楚地表现细节。但由于该算法考虑了16个像元点的值，且插值函数是三阶函数，因此计算量也明显增大。

2.4 正弦函数插值法

正弦函数插值法是对原始像元进行函数运算后用曲线将各个像元点连接起来，通过这个重建的函数求出任意位置处像元的灰度值。较其他插值方法，正弦函数法能有效减少插值所造成的信号损失，较好地保留形变场的有效信息。但是为了精确计算某一像元值，正弦函数插值需要覆盖无限多个点，这在实际应用中是无法实现的，并且大量的数据点导致插值过程十分耗时，而精度提高效果并不显著。

3 算例及结果分析

3.1 数据选择和InSAR处理

为了对上述4种插值算法进行统一的分析、比较及验证，本文选用2幅覆盖2003年12月26日伊朗巴姆地震的C波段 ENVISAT ASAR降轨数据和2幅覆盖2010年4月14日青海玉树地震的L波段ALOS PALSAR升轨数据(见表1)，采用高级雷达图像处理软件ENVI/SARscape(试用版)[8]进行两轨法差分干涉测量[9]，滤波方法选用较为健壮的Goldstein法[10]，相位解缠选用最小费用流法[11]。两例试验数据覆盖性好，相干性高，得到的干涉图连续完整(图2a、图3a)，试验流程如图1所示。通过设定相干阈值为0.5，即只对0.5以上的差分干涉图的相位值进行解缠，得到包含空值的试验形变场样本(图2b、图3b)，分别进行上述4种插值算法的内插与地理编码。

图1 SAR 影像处理流程图Fig.1 Flow chart of SAR image processing

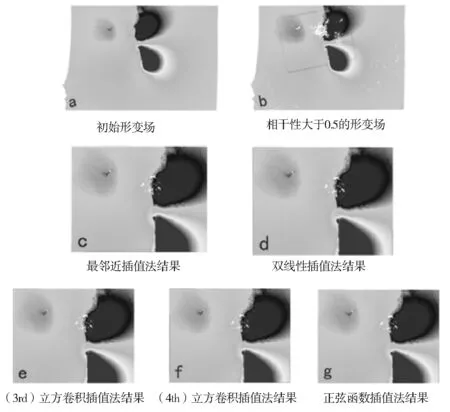
图2 2003年12月26巴姆地震InSAR结果及不同插值结果Fig.2 InSAR results and different interpolation results of the Bam earthquake on 26 December 2003

图3 2010年4月14日玉树地震InSAR结果及不同插值结果Fig.3 InSAR results and different interpolation results of the Yushu earthquake on 14 April 2010

3.2 插值结果分析对比

偏斜度和陡峭度分布是对统计数据分布形态对称性和陡缓程度的度量。从试验结果可以看出，地震造成的地物地貌破坏，在InSAR干涉图表现为低相干性，导致初始形变样本和实验样本之间数据分布形态明显差异，且形变场中空值越大，差异越大。表1为试验用SAR数据参数，表2、表3为不同插值算法的形变结果对比。

表1 试验用SAR数据参数Tab.1 SARdataparametersusedintests地震卫星波长/cm可探测最小形变量/m影像时间空间基线/m时间基线/d2003-12-26巴姆ENVISATASAR5.6(C波段)0.028VV2003-12-32004-02-11-3.069702010-04-14玉树ALOSPALSAR23.6(L波段)0.118HH2010-01-152010-04-17699.57492

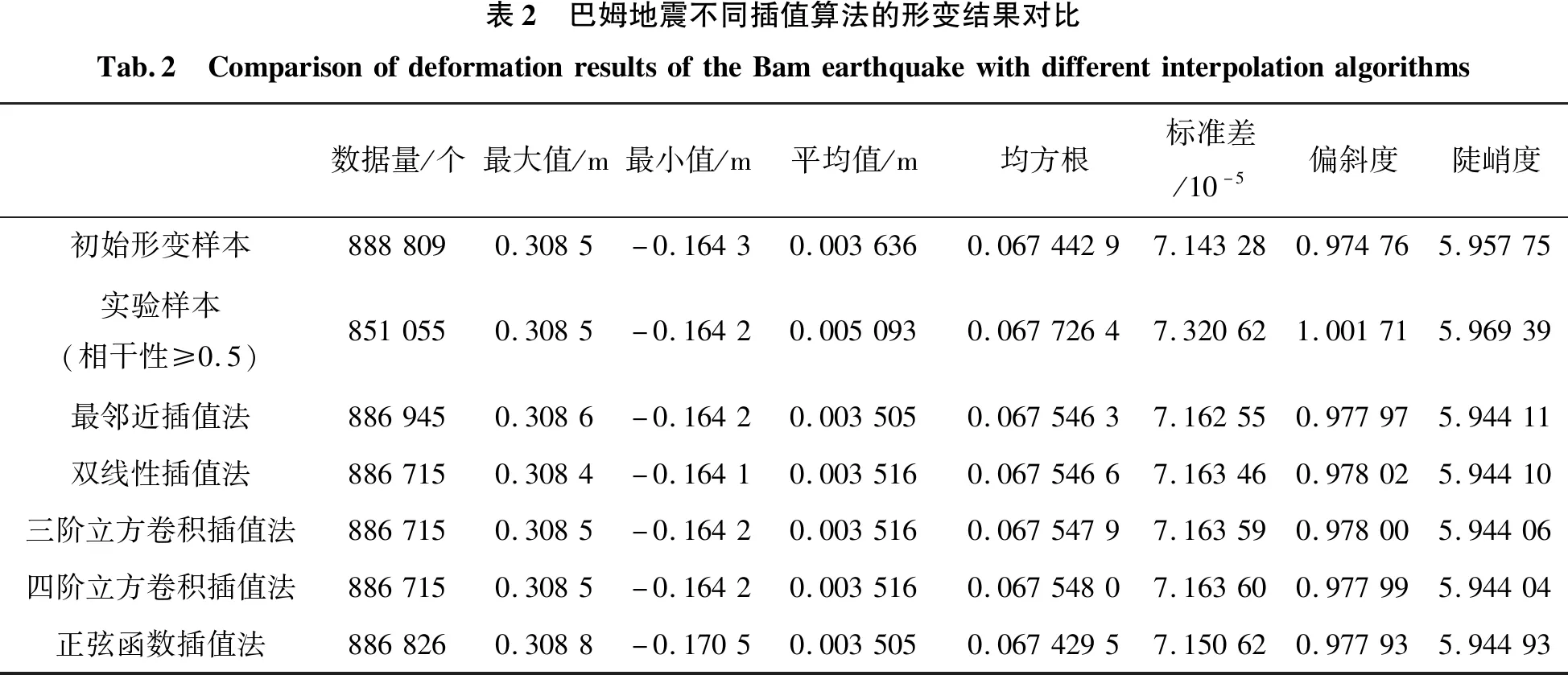
表2 巴姆地震不同插值算法的形变结果对比Tab.2 ComparisonofdeformationresultsoftheBamearthquakewithdifferentinterpolationalgorithms数据量/个最大值/m最小值/m平均值/m均方根标准差/10-5偏斜度陡峭度初始形变样本8888090.3085-0.16430.0036360.06744297.143280.974765.95775实验样本(相干性≥0.5)8510550.3085-0.16420.0050930.06772647.320621.001715.96939最邻近插值法8869450.3086-0.16420.0035050.06754637.162550.977975.94411双线性插值法8867150.3084-0.16410.0035160.06754667.163460.978025.94410三阶立方卷积插值法8867150.3085-0.16420.0035160.06754797.163590.978005.94406四阶立方卷积插值法8867150.3085-0.16420.0035160.06754807.163600.977995.94404正弦函数插值法8868260.3088-0.17050.0035050.06742957.150620.977935.94493

表3 玉树地震不同插值算法的形变结果对比Tab.3 ComparisonofdeformationresultsoftheYushuearthquakewithdifferentinterpolationalgorithms数据量/个最大值/m最小值/m平均值/m均方根标准差/10-4偏斜度陡峭度初始形变样本22392000.3315-0.4290.0621240.11427201.11013-2.007417.39076实验样本(相干性≥0.5)20050960.3245-0.49410.0460170.12460421.34053-1.608514.85072最邻近插值法22262580.3244-0.48080.0560890.12345741.27301-2.147097.32938双线性插值法22250180.3208-0.47640.0560060.12348551.27386-2.145287.31159三阶立方卷积插值法22250370.3257-0.47900.0560220.12351331.27413-2.144657.31145四阶立方卷积插值法22250360.3260-0.47960.0560220.12351611.27416-2.144577.31139正弦函数插值法22254340.3090-0.47920.0559680.12322561.27071-2.148297.33467

从内插结果来看，4种插值方法都使得干涉形变场连续清晰。但不同的插值方法对形变边缘梯度处理存在差异。由表2和表3所列的不同插值算法的形变结果对比可以看出，最邻近插值法的数据量最多，由于该方法只考虑最近的像元，因此最大值和最小值接近试验样本，平均值远小于试验样本，也小于初始样本，偏斜度与陡峭度也较其他方法与试验样本相差较大，在插值形变场边缘出现了明显的锯齿现象。双线性插值法是最邻近插值法的一种改进，基本克服了插值结果跳跃的缺点，其插值结果与离散程度较稳定，但是数据量最少，边缘和细节插值被抑制，出现轮廓模糊现象。三阶立方卷积插值法与四阶立方卷积插值法的结果较一致，最大值、最小值和平均值最接近初始样本，由于四阶收敛的核函数比三阶收敛的核函数更加接近于阶跃函数，因此四阶立方卷积插值法的结果较平滑，精度更加可靠。正弦函数插值法的数据量仅次于最邻近插值法，均方根和数据分布形态都最接近初始形变样本，但是最大值、最小值和平均值都与初始样本和实验样本差异较大。

4 结束语

InSAR干涉图的形变信息不全会对后续的分析反演结果产生不良影响，随着形变空值越多，反演破裂结果和真实地震破裂的差异越明显。为了提高形变场质量，将多种图像插值算法引进到InSAR处理过程中。本文利用4种常用的图像插值算法，通过真实震例进行试验对比分析，得到以下结论：

1)最邻近插值法只考虑最近的像元值，计算简单，但插值后的形变场边缘容易产生锯齿效应，造成形变值的不平滑。基于其算法原理，最邻近插值法特别适用于数据分类的抽样。

2)双线性插值法、三阶立方卷积插值法和四阶立方卷积插值法分别考虑周围4、8和16个像元。一般来说，高阶插值可以提供更好的结果。本文试验结果表明，双线性插值法插值的形变场边缘受到平滑作用，出现轮廓模糊现象，四阶立方卷积插值法与三阶立方卷积插值法的结果几乎无差异。

3)正弦函数插值法考虑其周围的256个像元，因此运算量会大大增加，数据数量、精度和分布形态都最接近初始形变样本，但是数据值与样本值差异较大。