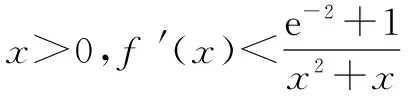解压轴题:等号与否 预测路径
许银伙 杨苍洲
(1.福建省泉州外国语中学 362000;2.福建省泉州第五中学 362000)
压轴题中经常出现不等式证明或由不等式求参数范围问题,它通常化为函数最值问题,然后综合运用函数或方程知识加以解决.但到底是化为一个函数还是化为两个函数呢?本篇介绍的方法是:由不等式是否含等号进行预测,如果含等号,通常可以构造不等式两边差的函数,直接由导数求最值解决;如果不含等号,通常变形,分别求不等式两边函数的最值,借助两边不同时取最值来得到原不等式成立,或者构造不等式两边差的函数,运用常用结论lnx≤x-1,ex≥x+1进行放缩,然后对放缩后的新函数式求最值.
例题1 (2014湛江质检)已知函数f(x)=sinx(x≥0),g(x)=ax(x≥0).
(1)若f(x)≤g(x)恒成立,求实数a的取值范围;

分析与解(1) 实数a的取值范围为[1,+∞).
(2)由已知得:

由(1)得:
h′(x)=x-sinx≥0对x≥0恒成立.

又因为φ′(0)=0,
∴φ′(x)>0对x>0恒成立,函数φ(x)对x≥0单调递增.
又∵φ(0)=0,∴φ(x)≥0对x≥0恒成立,所以问题得证.
反思与评注
1.问题(2)的不等式含有等号,因此考虑构造不等式两边差的函数,直接求导解决.
2.x-sinx≥0对x≥0恒成立(当且仅当x=0时取等号)是常用结论,但解答时还需证明.

(1)求函数f(x)的单调区间和极值;
分析与解



∴只需g(x)≤e对x∈(1,+∞)恒成立.
方法一直接讨论法






∴φ(x)对x∈(1,+∞)单调递增.
又φ(e)=e,
∴1 综上得:所求实数a的取值范围为(0,e]. 方法二分离参数法 反思与评注1.问题(2) 对于任意x1,x2∈(1,+∞),总有f(x1)≥g(x2)成立,等价于x∈(1,+∞)时,f(x)min≥g(x)max.∵f(x)不含参数,通常先求出f(x)min;g(x)含参数,问题解决通常转化为采用分类讨论或分离参数方法. 例题3 已知函数f(x)=ex-ax-1(a∈R),其中e为自然对数的底数. (1)若f(x)≥0对任意x≥0恒成立,求实数a的取值范围; 分析与解(1)实数a的取值范围为(-∞,1]. 当x∈(0,1)时,h′(x)<0, ∴h(x)在区间(0,1]单调递减; 当x∈(1,+∞)时,h′(x)>0, ∴h(x)在区间[1,+∞)单调递增. h(x)在(0,+∞)最小值为h(1)=0, ∴h(x)≥0得lnx≤x-1对x≥0恒成立. 问题得证. 反思与评注1.问题(2)是求和型不等式,且不含等号,因此考虑各项放缩后再求和.放缩的方向通常有两个:化为等比数列或化成可裂项相消的数列. 2. 问题(2)的解决借助了常用结论: lnx≤x-1对x≥0恒成立. (1)求证:曲线y=f(x)在点(1,f(1))处的切线不过点(2,0); (2)若在区间(0,1]中存在x0,使得f′(x0)=0,求k的取值范围; 分析与解(1) 略. (2)k的取值范围为[1,+∞). 由f′(1)=0得k=1. 当x∈(0,e-2)时,h1′(x)>0, ∴h1(x)在区间(0,e-2]单调递增; 当x∈(e-2,+∞)时,h1′(x)<0, ∴h1(x)在区间[e-2,+∞)单调递减. ∴h1(x)在(0,+∞)最大值为h1(e-2)=1+e-2. ∴h2(x)在区间(0,+∞)单调递增. 又h2(0)=e-2+1,则x>0时,h2(x)>h2(0)=h1(e-2)≥h1(x).问题得证. 反思与评注1.问题(3)要证明的不等式两端函数式都不含参数,且不含等号,通常不能左右两边相减构造新函数,利用导数直接求出最值解决,而是要变形,化为左右边两个函数,通过分别求它们的最值或值域解决问题.如果两边函数都能求出最值,通常不会同时取得最值. 参考文献: [1] 许银伙.意念引领攻克难题[J].福建中学数学,2015(8):40-42. [2]雷波. 函数结构任繁杂巧妙转化变通达[J].数学通报,2106(6):42-46.