以形助数 数形结合
周小微
(江苏省江安高级中学 226500)
数形结合思想是解数学题时常用的思想方法,可以把某些抽象的问题直观化,把抽象思维变为形象思维,从而利于把握数学问题的真谛.
一、数形结合,巧解方程
众所周知,方程自身或方程两边(或通过变形)的表达式有明显的几何意义,对于一些无法直接解决的方程问题,如果采用数形结合的思想,将抽象的数量关系转化为图形来解决,可以事半功倍地解决问题.
例1 实数p取什么值时,方程|x2-4x+3|=px有四个不同的实数根?


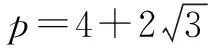
点评本题中的方程有明显的几何意义,即所构造的y=|x2-4x+3|与y=px两条曲线的交点的个数即为方程的实数根的个数.
二、数形结合,速求极值
三角函数是函数部分的一个重要内容,可以充分利用数形结合思想来研究其性质,把图象和性质结合在一起,即能够利用图象的直观性得出函数的性质,也能利用函数的性质来描绘函数的图象,这样既可以掌握函数的图象和性质,又可以熟练地利用数形结合的方法.



点评本题中三角函数的图象为数形结合带来了便利条件,从图象上寻找满足条件的定义域,找到对应的函数值常常是解决问题的关键.
三、数形结合,转化复数
数形结合法是解复数问题的常用方法,能够把复数问题变为几何问题,从而能够降低解题难度.用此方法解复数问题时要把握好复数的特征,充分认识到复数与几何、函数之间的关系,利用数形结合对复数问题进行转化,从而直接、快速地求解.
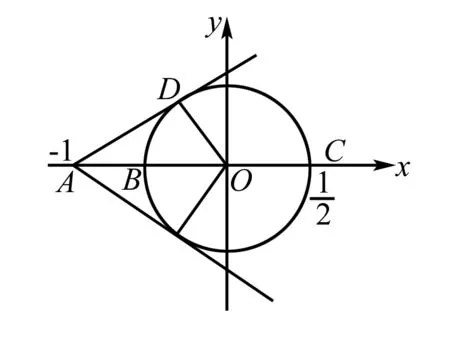

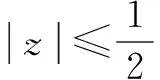
点评本题是利用复数在复平面内对应的图形及其几何意义来解题的.其几何意义包括与复平面内的点一一对应,还有与复平面内从原点出发的向量一一对应,因此可以从解析几何的角度来审视复数问题,可借助数形转换来解题.
四、数形结合,证明不等式
不等式问题一直是高考中的高频考点,而证明不等式的方法有很多,有基本不等式法、函数法等.运用数形结合法来证明不等式,透过不等式的性质发现其几何意义,构造相应的几何图形来阐述不等式,将抽象问题具体化,直观化.

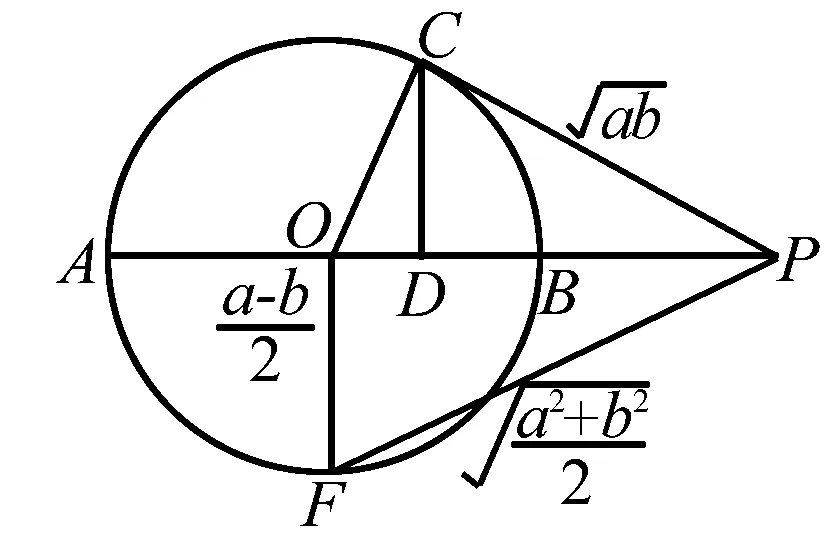

点评本题可以采用两种思路,从两种角度进行解题分析.一是采用基本不等式法,将不等式拆分,逐个进行证明;二是采用数形结合的方法,通过构造不同的平面的图形,从图形的角度直观化进行不等式证明.
数形结合方法可以用来解答各种难题,包括一些复杂函数的极值问题、方程问题、复杂的集合问题等等.在高中数学的教学过程中,应该立足教材,挖掘数学思想方法,从而优化教学内容,在讲解题目的过程中适当的介绍数形结合思想方法,提高学生解题能力.
参考文献:
[1]吕福刚.数形结合方法在数学教学中的应用探究[J].教育现代化,2017(34).
[2]王林.高中数学教学中数形结合方法的有效运用[J].科学大众(科学教育),2017(09).

