从一题多解谈向量问题的解决方法

邹司伟

(江苏省苏州实验中学 215000)

本文利用“一题多解”的理念，从不同角度分析解决一道习题，旨在帮助学生总结归纳向量问题的常用解法，激发学生的学习兴趣、培养学生勇于探索的习惯和敢于创新的能力.

一、向量分解法

设∠COA′=α，利用正弦定理得到：

=2cos(60°-α).

于是α=60°时x+y取最大值2.

或者使用余弦定理：

注意到∠CA′O=60°，从而得到等式：x2+y2-1=xy.

利用基本不等式易得x+y的最大值为2.

二、建系求解法

如图3建立坐标系：

由题意得

解得：

易知当α=60°时,x+y取最大值2.

三、内积求解法

如果从向量内积角度出发，我们可以通过内积的方法，将向量等式转化为数量等式，从而求解问题.

之后步骤类似方法二.

四、几何解法

而向量问题往往可以有几何解释，我们利用等和线的知识可以得到另一个解法：

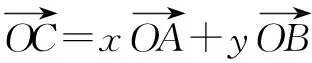
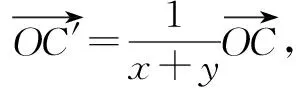
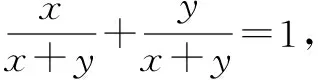
作出图形：

本题的几种解法中，解法一，四比较依赖图形的几何性质，而解法二，三更偏向于代数.

本题将圆替换为椭圆，圆的优良的几何性质丢失了，从而用向量分解或者几何转化的方法都解决不了.而通过坐标系或者内积，将问题代数化仍然有效.

观察问题，发现题目中有关键词“外心”，从而由外心的几何性质，联想到使用内积的方法将问题代数化后就能有效解决.

参考文献：

[1] 任燕.浅谈一题多解应注意的问题[J].速读旬刊,2016(10).

[2] 张轩.小议高中数学中的一题多解[J].魅力中国,2016(18).