用类比思想来认识初、高中几何的几个结论
周桂芸
(山东省淄博市第十七中学 255033)
立体几何是几何学的重要组成部分,对高中学生来讲,学这部分内容的基础是初中的平面几何,教学中注重把平面几何的知识推广到空间中来,采用类比推广的方式,从二维平面过渡到三维空间,对突破教学难点,开拓学生的思维的广度非常重要.下面看几个例子.
一、等边三角形的内切圆与外接圆(二维平面)和正四面体的内切球与外接球(三维空间)
平面几何中: 等边三角形有且只有个内切圆与一个外接圆,其圆心为等边三角形的中心.

如图1等边△ABC的边长为a,则有以下四个结论:
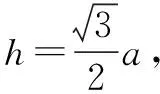
空间几何中:正四面体有且只有一个内切球和一个外接球,其球心是正四面体的中心.如图2若正四面体的棱长为a,亦有上述类似的四个结论:

下面求解一下.如图2,过A作AO′⊥面BCD,垂足为O′.连结O′D.
在Rt△AO′D中:
∴正四面体的高
设正四面体的中心为O,则O即为其内切球的球心,亦为外接球的球心,且OA=OD=R,OO′=r.
在Rt△OO′D中:OD2=OO′2+O′D2,


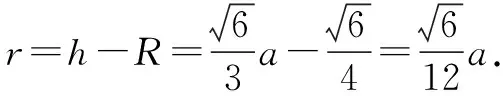
由此得出:R=3r.
二、正方形的内切圆和外接圆(二维平面)与正方体的内切球和外接球(三维空间)
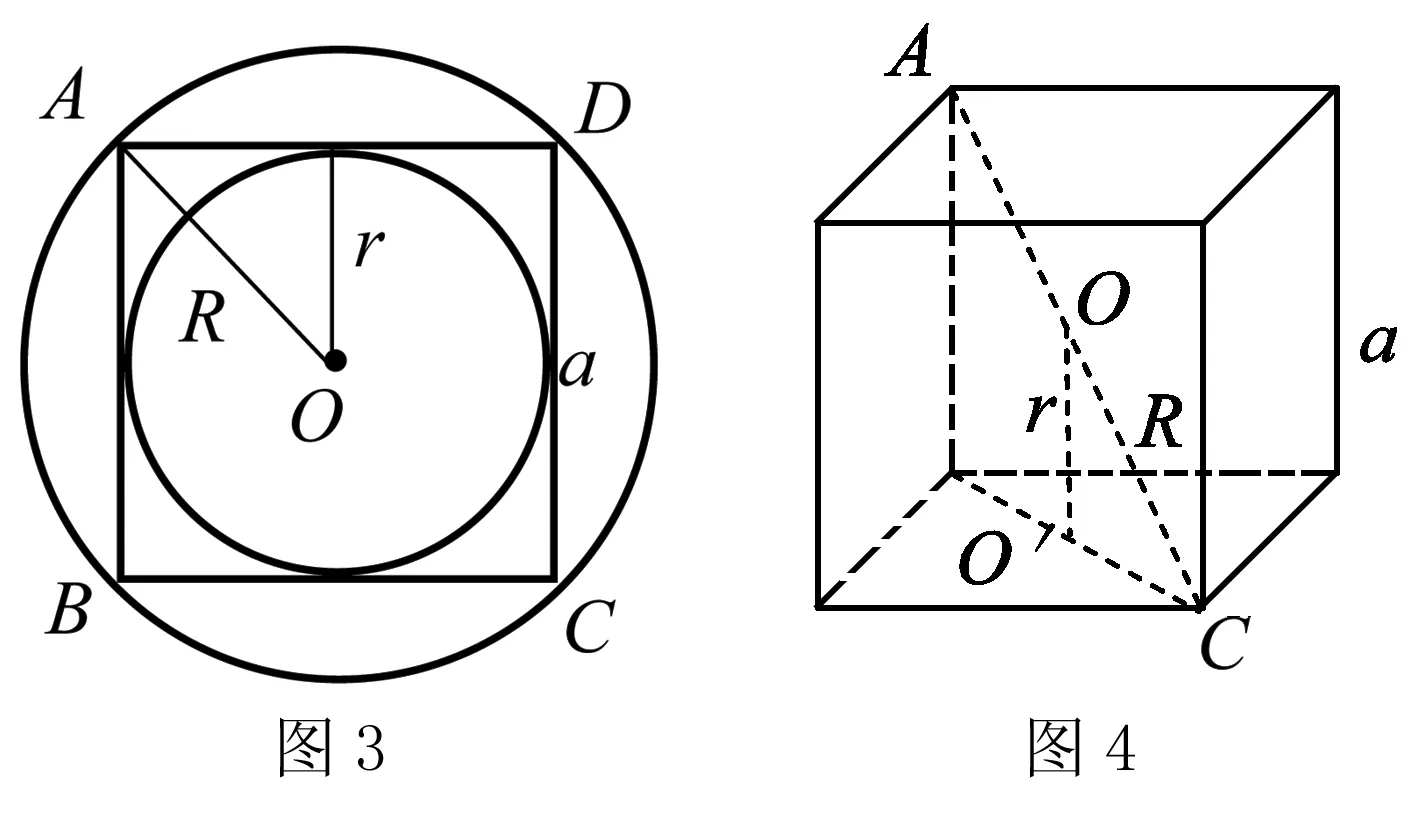
空间中:(如图四)正方体中:

三、平面中,正三角形内的任一点到各边的距离和为定值;正四面体内任一点到四个面的距离和为定值
空间中:正四面体的四个面面积为S,体积为V,在四面体内任取一点P,P到各面的距离分别为h1、h2、h3、h4,求证:h1+h2+h3+h4是定值.
分析高一学生在做此空间题目时,几乎无从下手,但只要回顾平面几何中的证法,学生深受启发,对比如下:

简证在平面中
S△ABC=S△APB+S△BPC+S△APC,

∴h1+h2+h3=h为定值.
空间中:V=VP-ABC+VP-BCD+VP-ACD+VP-ABD,

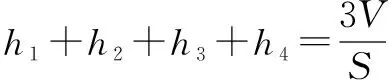
四、平面中的勾股定理推广到空间中是什么结论呢
二维平面 → 三维空间
图形推广:
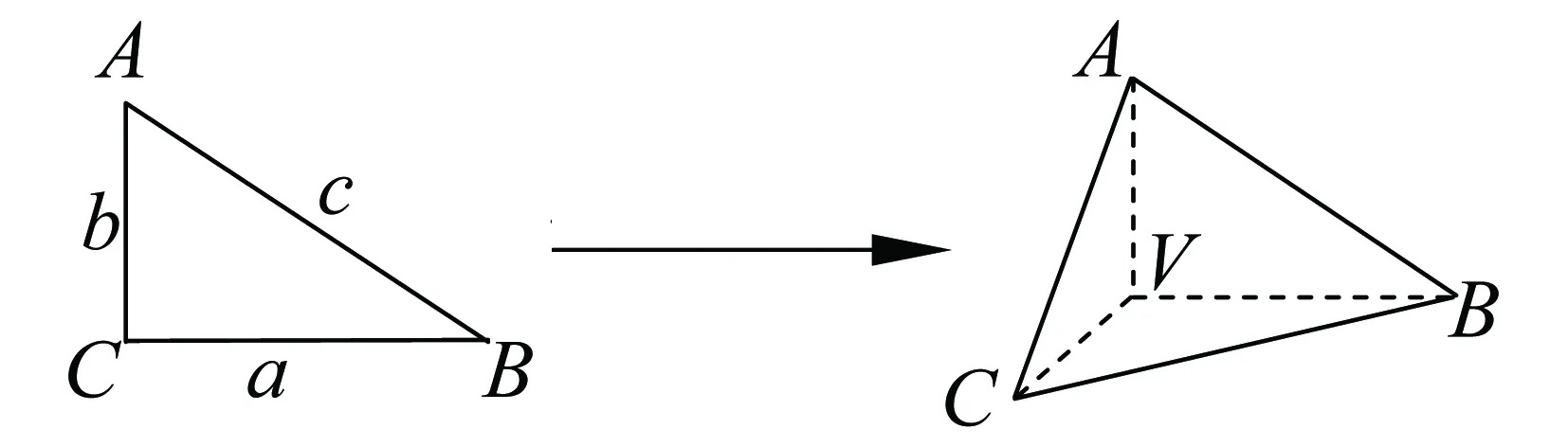
直角三角形→三条棱两两垂直的棱锥

有以上知识做铺垫、渗透,学生能写出结论猜想,这是一非常正确的结论.其证明方式很多,现介绍一种(教学中,此证明仅供有兴趣的学生参考).
如右图:由VA、VB、VC两两垂直,
既得出面VAB、面VBC、面VCA两两垂直;
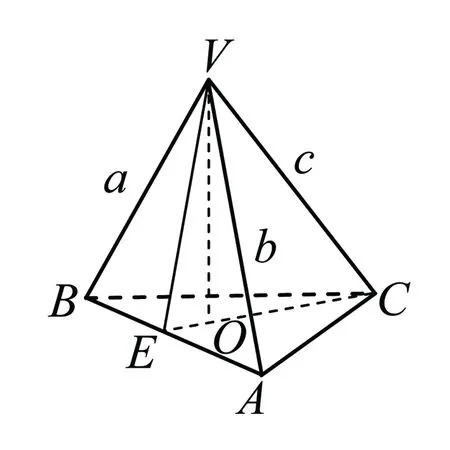
作VO⊥面ABC,连接CO并延长交AB于E.由VC⊥VB,VC⊥VA,可知:VC⊥面VAB,由VE⊂面VAB可知:
VC⊥VE,△VEC为直角三角形.

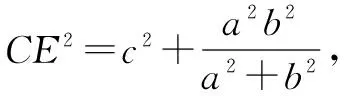
∴△ABC的面积的平方为:
证毕.
教学中运用这类比的思想,从二维空间到三维空间加以渗透,启发学生独立思考.大胆猜想,然后严密证明,这符合数学思维训练要求.我们在教学中要善于发现知识的内在联系,多给学生一些有益的启发,然后指导学生去思考、去发现.
参考文献:
[1]王瑾,贺贤孝.数学证明与数学发现[J]. 数学通报,2000(10).
[2]罗增儒.数学证明的作用[J]. 中学数学教学参考,2001(05).

