圆锥曲线的解题方法探析

徐 博

(吉林省德惠市实验高中二年七班 130300)

由于圆锥曲线解题过程比较复杂，许多同学对此感到解题困难，这主要是由于没有掌握圆锥曲线的解题方法策略与技巧.圆锥曲线的解题方法技巧不少，需要掌握多种方法策略，这样才能在解题时灵活运用，从而提高解题效率.

一、运用化归方法解题，能够降低解题难度

在遇到复杂的圆锥曲线问题时，可以运用化归的思想方法，把所求的问题转化成简单的问题，这样就能有效降低解题难度.虽然圆锥曲线具有复杂性和综合性特点，但是圆锥曲线解题本质是用代数方法来解决几何问题，实际上是把几何问题与代数问题进行了相互转化.运用化归的数学思想方法，就能容易解决复杂的圆锥曲线问题.

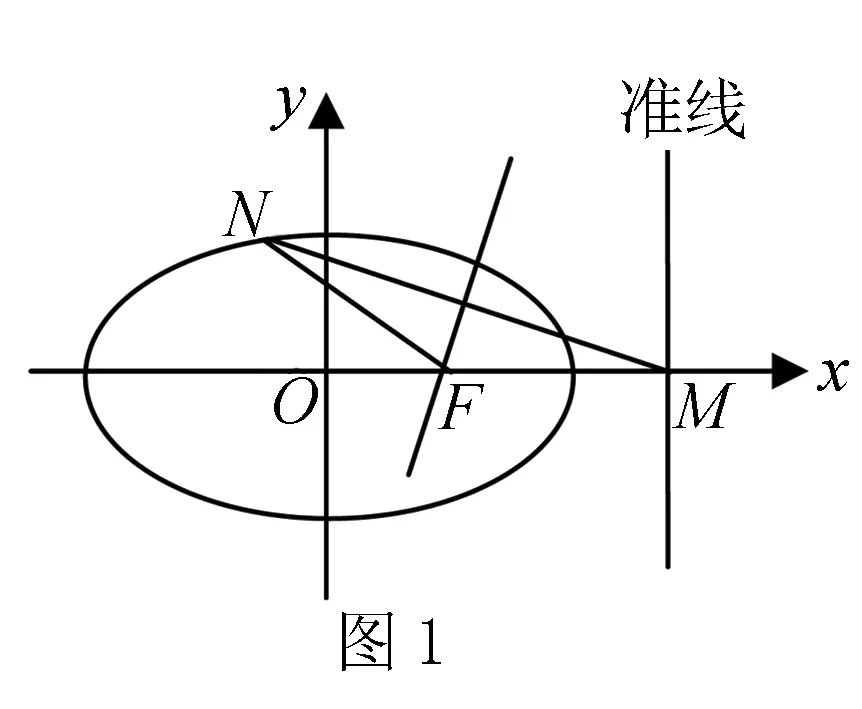
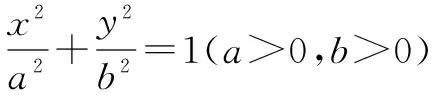
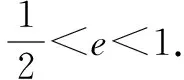
点评在求解此题时许多同学对此没有思路，是因为对题目中的条件：“在椭圆上存在一个点N，能使MN线段的垂直平分线经过点F.”不能进行有效的转化，造成解题困难.如果能把上述条件转化成：“在椭圆上存在一点N，使得MF=NF.”这样就能使题目容易解决.

二、运用分类讨论方法，能够全面综合解题

在解题时遇到多种情况，需要对题目进行分类讨论，对每一种情况进行逐个求解，然而进行综合归纳，就能提高解题的全面性和综合性，使解题的过程既不遗漏也不重复.

(1)求出椭圆的方程.

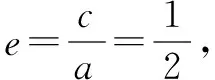
(2)本问可用多种方法求解.

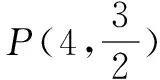
点评本题虽然假设了A、B两点的坐标，但是并不求解，而是运用韦达定理进行求解，这样能简化计算过程.由于题目中所给的直线方程l中含有参数m，直线方程不确定，一般情况下需要分情况进行讨论，而直线l与x轴垂直是一种特殊情况，假如垂直时l2直线存在，它肯定符合上述情况，可通过特殊情况找出该直线，然后再验证该直线是否符合题意.

三、运用向量方法解题，创新解题方法技巧

运用向量的方法解决圆锥曲线问题非常方便快捷,解题时应遵循三个步骤：先将圆锥曲线问题转化成向量问题，利用向量进行计算，最后再把向量计算的结果转化成圆锥曲线问题.其中的把圆锥曲线问题转化成向量问题是该方法应用的关键.

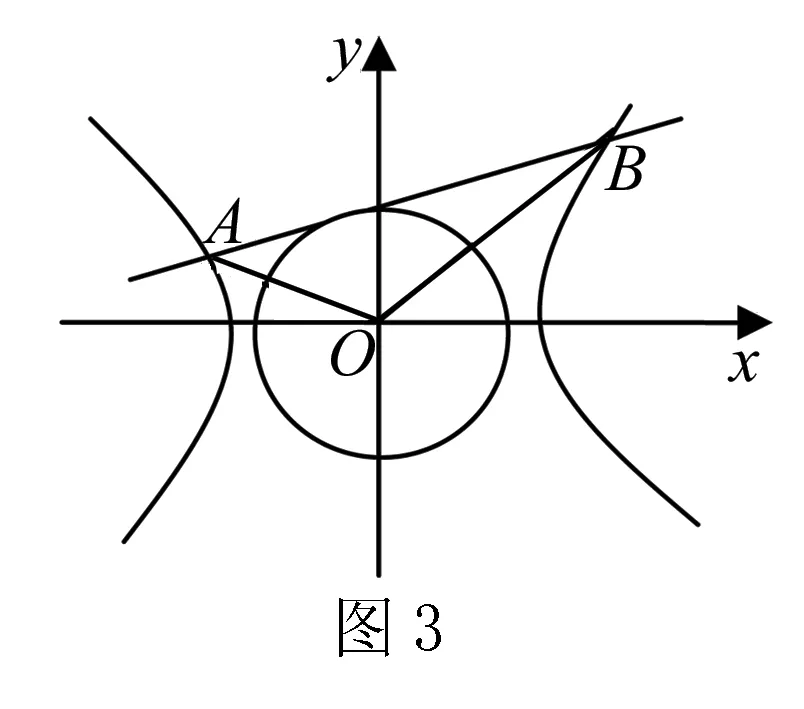
(1)求双曲线方程.

(2)已知圆O方程是：x2+y2=2，在其上有一个动点P(x0,y0),(x0y0≠0)，过P点的切线l与双曲线相交于A、B两点，求证：∠AOB的大小为定值.

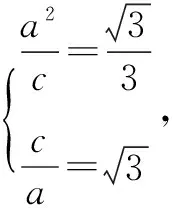
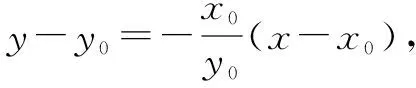
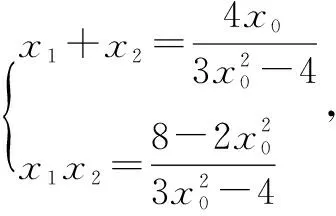
∴可证明两向量垂直，即∠AOB=90°.

点评运用向量的加法、减法及其几何意义、平面向量的数量积及其几何意义来解决圆锥曲线问题非常方便快捷，因此，应注重发挥向量在圆锥曲线解题中的应用，从而提高解题效率.

总之，要提高圆锥曲线的解题效率，就要掌握解题的多种方法和技巧并加以灵活运用，才能高效解题，由于圆锥曲线解题的方法较多，本文只选取了三种，希望能起到抛砖引玉的作用.

参考文献：

[1] 赖春葵.高中数学圆锥曲线教学及在解题中的应用探析[J].数学学习与研究, 2015(3).

[2] 戴锦权.从考题探析圆锥曲线题解题策略[J].理科考试研究,2013(13).