数列典型错解剖析

柳 华 商俊宇

(1.山东省临沂市中医药职工中等专业学校 276000;2.山东省临沂第十八中学 276017)

数列是高中数学的重要内容之一，也是今后学习高等数学的基础，因此成为历年高考考查的重点与热点.但是学生在解题时往往出现这样或那样的错误，造成不必要的失分现象.

一、忽视n的取值范围导致错误

例1 已知an=n2+λn(n∈N*)，且数列{an}为递增数列，求实数λ的取值范围.

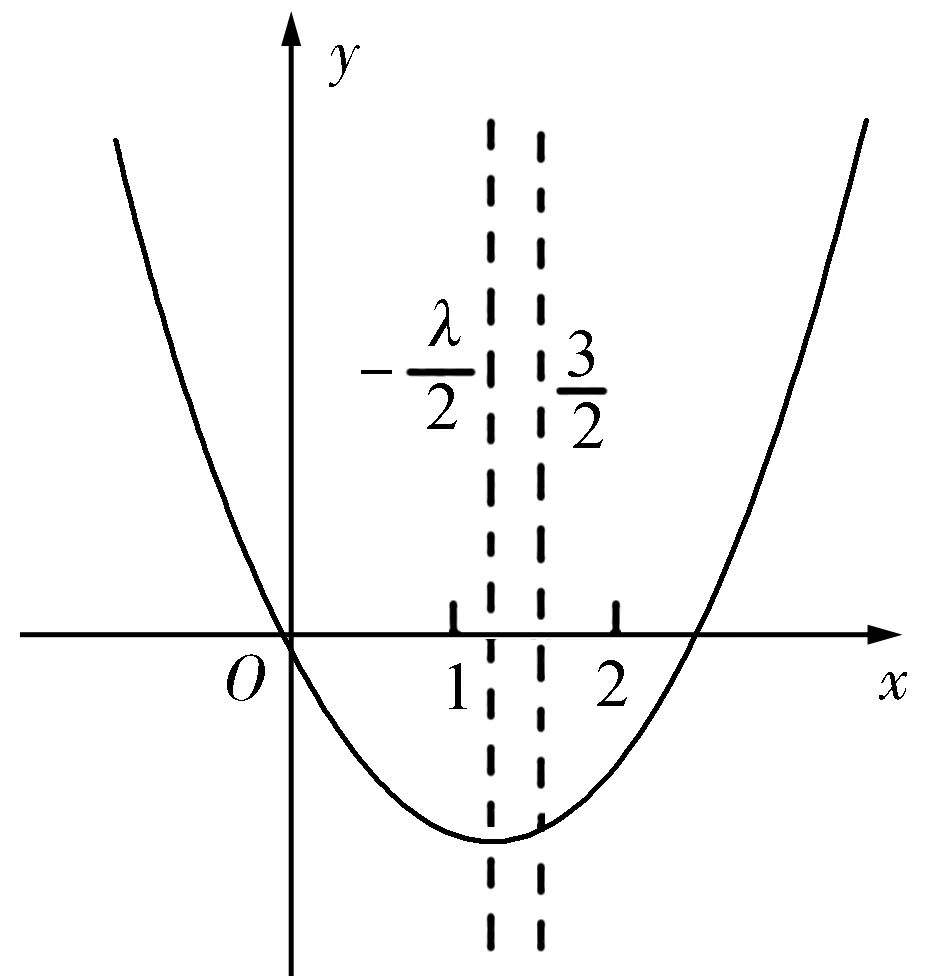
图1

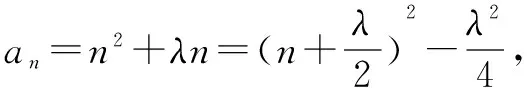
得到an=n2+λn在[1,+∞)上是单调递增函数.

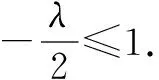
得λ>-3，即为所求实数λ的取值范围.

正解二由题意an+1>an对任意n∈N*恒成立，即(n+1)2+λ(n+1)>n2+λn

化简得λ>-(2n+1)，因为-(2n+1)max=-3，

因此λ>-3，即为所求实数λ的取值范围.

二、利用an=Sn-Sn-1求通项公式时忽视n≥2导致错误

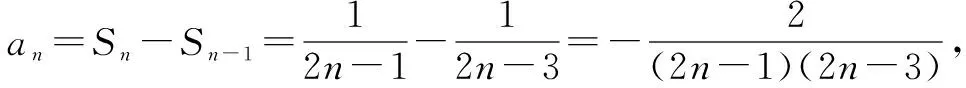
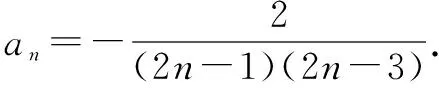
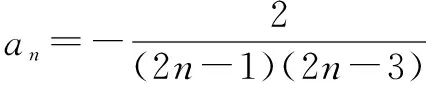
正解当n=1时，a1=S1=1；

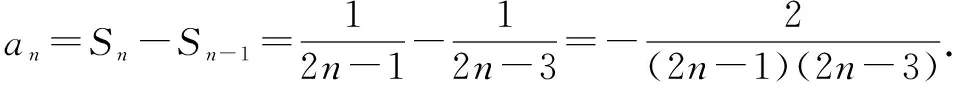
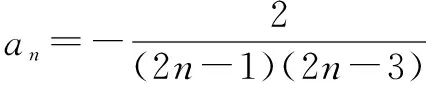
三、忽视等比数列中隔项同号原则导致错误

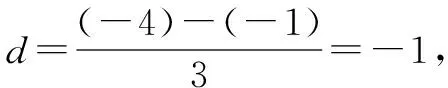
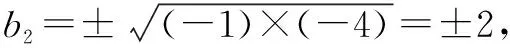
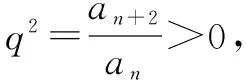
正解设等差数列的公差为d，则

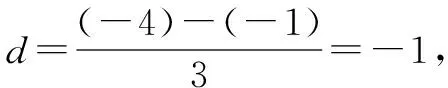
四、等比数列求和中忽视q=1导致错误

例4 求和1+3a+5a2+…+(2n-1)an-1.

错解令Sn=1+3a+5a2+…+(2n-1)an-1①,

则aSn=a+3a2+…+(2n-3)an-1+(2n-1)an②.

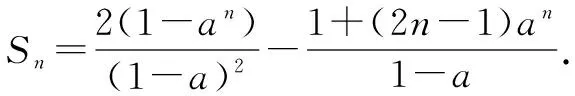
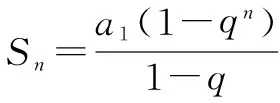
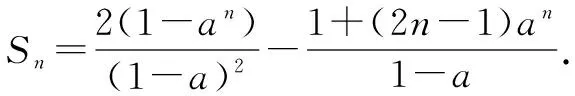
五、忽视等比数列中各项不为0导致错误

例五若a，b，c，d成等比数列，试判断a+b，b+c，c+d是否构成等比数列.

错解设等比数列a，b，c，d的公比为q，则

a+b=a(1+q)，b+c=aq(1+q)，c+d=aq2(1+q)

所以a+b，b+c，c+d构成首项为a(1+q)，公比为q的等比数列.

错因上述解答中a≠0，q≠0是显然的，但是当q=-1时，1+q=0是可能的，故解答错误.

正解当1+q=0时，a+b=b+c=c+d=0，故a+b，b+c，c+d不能构成等比数列.

1+q≠0，能构成首项为a(1+q)，公比为q的等比数列.

六、公比设法不当致错

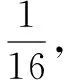
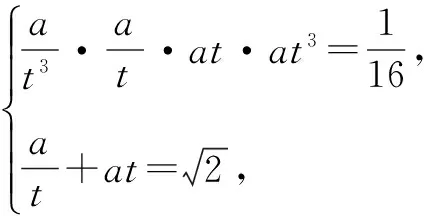
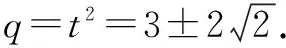
错因上述具有对称性的设法不失为一种好的设法，在等差数列中也很方便，但在等比数列中只有当这几个数为同号时方可使用.上述设法的公比为q=t2>0，但实际上q可以为负数.

正解设这四个数为a，aq，aq2，aq3，

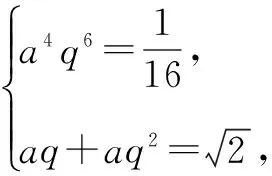
七、忽视隐含条件导致错误

错解由条件a，1，c成等差数列，得a+c=2；

又由a2，1，c2成等比数列，得a2c2=1，即ac=±1.

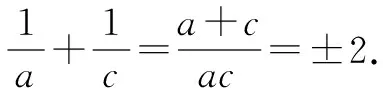
错因题设条件中a，1，c是三个不同的实数，若ac=1，结合a+c=2，得a=c=1，不合题意.故只有ac=-1.

参考文献：

[1]王怀学，肖斌. 高考数学经典题型与变式[M].拉萨：西藏人民出版社，2016.