体现在概率统计下的数学核心素养

寇桂晏 陈国林

(赣南师范大学科技学院 341000)

数学核心素养的提出，受到了很多人的高度关注，本文主要对有关概率考题方面进行研究归纳，希望能够给读者帮助.

一、以生活为背景进行考查

例题1 (2016重庆巴蜀中学月考)2014年12月28日开播，北京市公共电汽车和地铁按照里程分段计价，具体如下表(不考虑公交卡折扣情况)

乘公共电汽车方案10千米(含)内2元;10千米以上部分,每增加1元可乘坐5千米(含)乘坐地铁方案(不含机场线)6千米(含)内3元;6千米至12千米(含)4元;12千米至22千米(含)5元;22千米至32千米(含)6元;32千米以上部分,每增加1元可乘坐20千米(含)

已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5元，现从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选出120人，他们乘坐地铁的票价统计图如图所示.

(1)如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1人，试估计此人乘坐地铁的票价小于5元的概率；

(2)已知选出的120人中有6名学生，且这6人乘坐地铁的票价情形恰好与按票价从这120人中分层抽样所选的结果相同，现从这6人中随机选出2人，求这2人的票价和恰好为8元的概率；

(3)小李乘坐地铁从A地到陶然亭的票价是8元，返程时，小李乘坐某路公共电汽车所花交通费也是8元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为40千米，试写出路程s的取值范围.

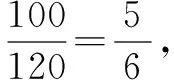
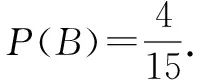
( 3 ) 乘公共电汽车方案的里程： 10 千米内(含) 2 元， 10 千米以上部分，每增加 1 元可乘坐 5 千米(含) ; ∴10+5×2

评注本题以实际生活背景为素材进行考查，由统计图表可以看出，120人中票价为3元、4元、5元的人数分别为60,40,20,因此易得票价小于 5 元的概率；根据比例知 6 名学生中票价为 3 元、4 元、5 元的人数分别为 3,2， 1，可把这6人编号为a,b,c,d,e,f，通过列举法知其中任取2人有15种情形，2人的票价和恰好为8元的有4种，由概率公式计算可得概率;(3)分别计算乘公共电汽车和地铁的票价为5元时的里程，其公共分部即为所求．

二、以生产产品为背景进行考查

例题2 (2016山东实验中学月考)从编号为0，1，2，…，79的80件产品中，采用系统抽样的方法抽取容量是10的样本，若编号为58的产品在样本中，则该样本中产品的最大编号为( ).

A．78 B．76 C．74 D．72

解析由题意得样本间隔为8，因此最大编号为58+16=74，选C.

评注本题以生产产品为背景考查了系统抽样，首先应该明确所得样本之间的间隔为多大，理解系统抽样是如何进行抽取的，方能对此题进行解决.

三、以当前有关时事为背景进行考查

例题3 2016年10月17日7时30分在中国酒泉卫星发射中心成功发射了神舟载人飞船，意味着我国航天事业进一步得到了提高和发展，为了提高中学生的科普兴趣，某校特举行了科普知识竞赛，结合甲、乙两名学生的6次成绩(百分制)制成了如图所示的茎叶图：

(1)若从甲、乙两名学生中选择1人为该知识竞赛的一等奖获得者，你会选哪位？请运用统计学的知识说明理由；(2)若从学生甲的6次培训成绩中随机选择2个，记选到的分数超过87分的个数为ξ，求ξ的分布列和数学期望．

(2)ξ的所有可能取值为0，1，2，则

ξ012P25815115

评注本题主要结合了当下时事考查了茎叶图、平均数、方差、离散型随机变量的分布列和数学期望等基础知识．第1问，通过茎叶图可以得出甲和乙的平均成绩，在平均成绩相等的情况下方差越小，发挥越稳定；第2问，先从茎叶图中读出6个数，其中超过87分的有2个，先计算出ξ=0,1,2三种情况的概率，列出分布列即可计算数学期望．

四、以数学文化为背景进行考查

(1)求选手甲第一关闯关成功且所得学豆为零的概率;

(2)设该学生所得学豆总数为X，求X的分布列与数学期望.

解析(1)设甲“第一关闯关成功且所得学豆为零”为事件A，“第一关闯关成功且第二关闯关失败”为事件A1，“前两关闯关成功且第三关闯关失败”为事件A2，则事件A1，事件A2为互斥事件.

(2)X所有可能取值为0，5，15，35

所以X的分布列为：

X051535P7163818116

评注本题以国际数学节和我国古代数学家祖冲之的圆周率为背景，这类命题模式较为新颖，应引起注意和思考.通过本题发现考查的内容依旧是我们很熟悉的高中知识点，因此要掌握这种题型必须熟练掌握有关概率统计的基本知识.

参考文献：

[1]陈国林.文化素养下的概率统计考查[J].高中生之友，2017(4)：28-30.