基于遗传算法的二维最大类间方差法的优化

， ，

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

在计算机视觉理论中，图像分割、特征提取和目标识别是由低层到高层的3大主要任务，特征提取和目标识别都是以图像分割为基础。目前的图像分割方法主要有基于阈值的分割方法、基于边缘的分割方法、基于区域的分割方法和基于特定理论的分割方法等。阈值分割法因对图像的质量要求较低，而且运算过程相对简单，效果较好，所以在图像分割中应用最为广泛。常用的阈值分割法中，最大类间方差法因计算简单、运算效率高、速度快且得到的阈值较为准确，得到了广泛应用[1]。

但最大类间差法的缺点也显而易见，对于目标和背景相差不大的图像，灰度直方图呈现双峰或多峰的情况，使用此方法很容易导致图像的信息丢失，处理时也只是考虑到了图像的灰度信息而没有考虑其空间信息，因此分割后图像上目标的轮廓在细节上会比较模糊。所以对分割后图像质量要求较高的情况，一维最大类间方差法显然是不能满足要求的[2]。针对一维阈值法的不足，二维最大类间差法引入了邻域平均灰度信息和像素信息一起构成二维直方图，通过二维直方图求解最佳阈值，其准确性和鲁棒性得到了很大提升，但与此同时，计算量也成指数形式增长，实时性大打折扣[3]。在此，针对二维最大类间差法存在的问题，将最佳阈值的判别式由二维降到一维，减少计算量，同时通过遗传算法加快寻优过程，减少了原有穷举法所带来的计算量过大的问题。

1 二维最大类间方差法

设大小为M×N的图像在像素点(x,y)处像素为f(x,y)，灰度级为L，以(x,y)为中心点的k×k(k取奇数)的邻域的平均灰度值g(x,y)为该点的平均灰度值，其灰度级也为L。f(x,y)和g(x,y)共同组成了一幅图像的二维直方图。图1为一幅测试图像的二维直方图(Z轴为像素点个数)。由图1可以看出，大部分的点灰度值与其邻域灰度值相差不大，集中在对角线上，远离对角线的点可能是灰度变化较大的边界点和噪声点。图2为二维直方图的平面投影图，假设(s,t)为最佳阈值将投影图分割成4个部分，其中沿对角线方向上A区域和B区域内元素相近，可分别看作是目标和背景，远离对角线方向的C区域和D区域可看作是边界点和噪声点。

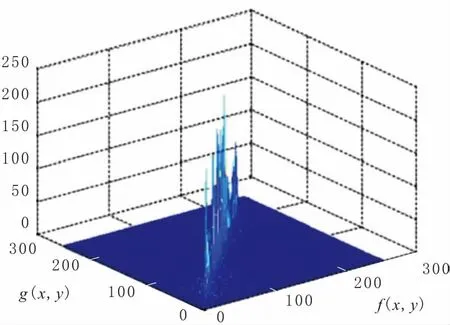
图1 测试图像的二维直方图

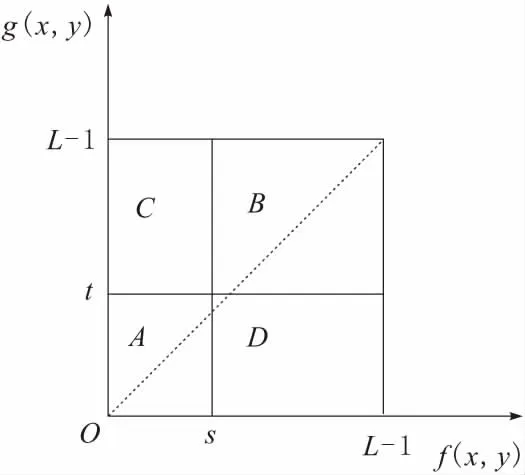
图2 二维灰度直方图的投影

记Cij为灰度值为i,邻域平均灰度值为j的像素点在整幅图像出现的频数，其相应的概率密度为Pij，则Pij的计算公式为：

(1)

根据阈值分割的思想，把图像中的像素点分为目标和背景两类(对应投影图中的A区域和B区域)，PA和PB是像素点出现在这两类区域的概率，则有：

(2)

(3)

A区和B区对应的均值矢量为：

μA=(μAi,μAj)τ=

(4)

μB=(μBi,μBj)τ=

(5)

二维灰度直方图的总均值矢量为：

μ=(μt,μj)τ=

(6)

实际情况下，边界点和噪声点所占的比例很小[3]，大多数情况，目标和背景所占的比例的统计值为0.95～0.98。所以有PA+PB≈1，且有μ≈PAμA+PBμB，在忽略边界点和噪声点的情况下等式成立。定义目标类和背景类的离散测度矩阵为σ，有

σ=PA(μA-μ)(μA-μ)τ+

PB(μB-μ)(μB-μ)τ

(7)

计算离散度矩阵的迹作为目标类和背景类的离散度的测度

tr(σ) =[PA(μA-μ)(μA-μ)τ+

PB(μB-μ)(μB-μ)τ]=

PA(s,t)(μAi-μi)2+(μAj-μj)2〗+

PB(s,t)(μBi-μi)2+(μBj-μj)2〗

(8)

使tr(σ)取得最大值时的阈值(s*,t*)即为随求的最大阈值，即

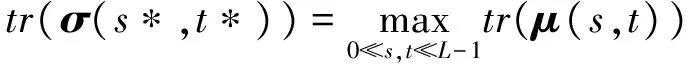
(9)

二维最大类间方差法引入像素的邻域灰度信息，通过二维直方图求得最佳阈值，和一维阈值法相比，其抗噪性和准确性显著提高，与此同时，算法的复杂度也成倍上升。其运算过程需要遍历整个图像存在的灰度值，离散度矩阵的计算需要双重循环，循环体需要在A区和B区做累加运算，次数为s×t+(L-s)×(L-t)，所以其运算复杂度为O(L4)。为了提高效率，可以从两方面入手：一方面可以简化其离散度矩阵，减少运算复杂度；另一方面可以加快寻优过程，减少计算量。

2 改进的二维最大类间差法

为了解决算法的计算复杂度问题，本文采用基于二维离散随机变量的边缘概率分布的改进算法[4]，对概率密度Pij求其边缘概率Wi和Wj。

(10)

(11)

Wi为像素灰度值i的一维直方图分布，Wj为邻域灰度值j的一维直方图分布。由一维最大类间方差法的定义可以推导出Wi和Wj的类间方差。

(12)

(13)

因为边界点和噪声点所占的比例很小，所以假设C区和D区的概率为零，即有

(14)

将式(14)代入式(2)，可推出

(15)

(16)

所以有:

PA=PAi=PAj

(17)

同理，将式(14)代入式(3)，可得:

PB=PBi=PBj

(18)

将式(17)和式(18)代入式(8)，有

tr(σ)=PA(s,t)(μAi-μi)2+(μAj-μj)2〗+

PB(s,t)(μBi-μi)2+(μBj-μj)2〗=

PAi(μAi-μi)2+PBi(μBi-μi)2+

PAj(μAj-μj)2+PBj(μBj-μj)2=

(19)

由式(19)可知，在忽略边界点和噪声点的情况下，二维最大类间方差法求最佳阈值的求解问题可以拆分成求解2个一维阈值之和的形式，复杂度大大降低，增强了时效性。

3 自适应遗传算法

在遗传算法中，交叉概率和变异概率的选取是影响遗传算法收敛速度和寻优结果的重要因素[5]。Srinvivas等提出的自适应遗传算法中，每一代的交叉和变异概率都会随着其适应度在每代中的大小而自动调整，使得在保持种群多样性的同时也保证了遗传算法的收敛性。自适应遗传算法的交叉概率Pc和变异概率Pm如下：

(20)

(21)

fmax为每一代种群中的最大适应度值；favg为每一代的平均适应度值；f为变异前的个体适应度值；f′为交叉的2个个体中适应度值较大的个体适应度值；k1,k2,k3,k4为(0,1)之间的调整系数。

从式(20)和式(21)可以看出，当个体适应度值越接近最大适应度值时，交叉和变异的概率越小，当与最大适应度值一致时其交叉和变异的概率为零。这在群体处于后期的时候是可以的，但在进化初期，容易导致适应度高的个体几乎处于不变的情况，而使得进化过程陷入局部最优解，显然这是需要避免的[6]。所以在自适应遗传算法的基础上，需要对交叉和变异的概率做进一步调整，在保证遗传多样性的基础上，避免进化趋于局部最优解。调整后的交叉概率Pc和变异概率Pm如下：

(22)

(23)

Pc0是最大交叉概率；Pm0是最大变异概率。如式(22)和式(23)所示，一方面交叉和变异概率随种群的适应度实现自动调整，更好地保留适应度高的个体，另一方面交叉和变异的概率不会为零，避免了陷入局部最优解的问题。

遗传算法的流程如图3所示。其主要步骤归纳如下：

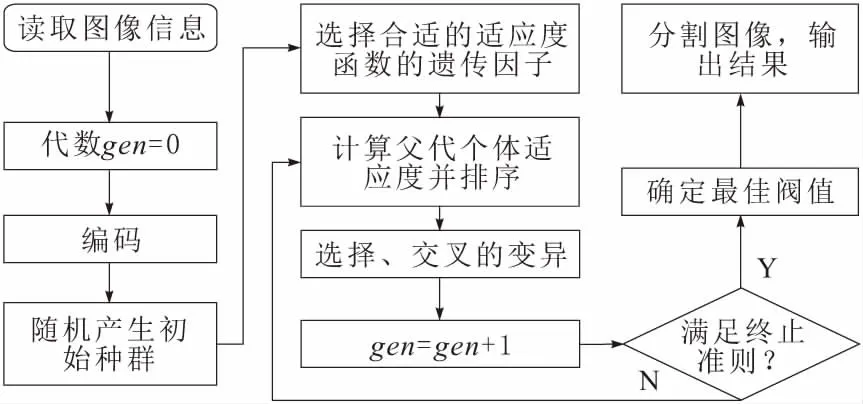
图3 遗传算法流程

a.编码。因为灰度值得范围是0～255共256(28)个灰度级，通常采用二进制编码的方式，又有(s,t)2个变量阈值，所以编码为16位，其中前8位表示像素点的阈值s，后8位表示邻域阈值t。

b.随机产生初始种群。初始种群的规模将影响算法的精度和效率。种群规模太小则搜索空间有限，种群规模太大将增加计算时间。本文的种群规模为20。

c.选择适应度函数。选择式(19)作为适应度函数计算适应度值。

d.选择、交叉和变异。采用轮盘赌作为选择方法。对前8位和后8位采用双点交叉，交叉和变异的概率如式(22)和式(23)所示，取Pc0=0.9，Pm0=0.1。

e.终止准则。当算法执行到最大代数或经过20代进化后，群体中最高适应度值仍未发生变化，则该个体即为所求阈值编码。本文实验确定最大遗传代数为100代较为合适。

4 实验验证

为了验证算法的正确性，分别采用经典Otsu法、遗传算法和本文算法对图片进行分割。实验的图片样本为PCB板，分割结果如图4所示。

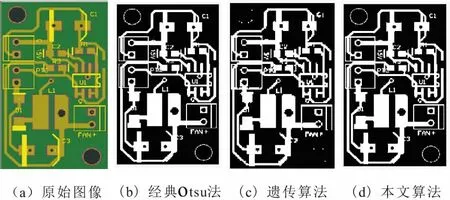
图4 各类方法图形处理后的对比

3种算法的阈值以及运行时间结果如表1所示。对分割结果进行分析可以发现经典二维Otsu法和本文算法的分割效果较好，且差距不大，遗传算法的分割效果相对较差，处理结果可以看出丢失了一些目标信息。由表1可知，和经典二维Otsu算法相比，本文算法在处理速度上大大提高，比经典算法的运算时间节约50%左右，且稳定性相比经典算法也有所提升。遗传算法的稳定性和经典算法相差不大，但阈值的精确性有所下降，运行速度提升的也很有限。综上所述，本文算法在运算速度上较之经典算法有很大提高，稳定性也有所提升。

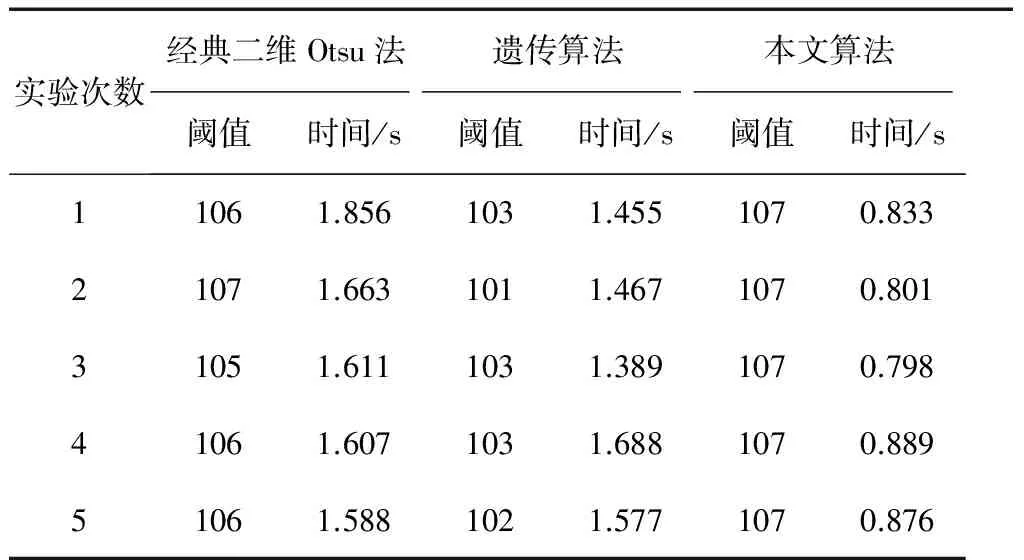
表1 不同方法的图像阈值及运行时间

5 结束语

针对经典二维最大类间方差法存在的复杂度高，运行时间长的问题，首先通过近似将原有的二阶离散度矩阵拆分成2个一阶的类间差之和，减少了运算难度，同时引入遗传算法，将原有的穷举法搜寻最优解改为由遗传算法进行寻优，加快寻优过程，进一步提高运算效率。实验证明，本文算法较之经典算法，效率上有较大提升，运算时间减少约50%，同时，在保证精确度的同时，稳定性也有所提升，使最终结果稳定在2个像素，大大改善了经典算法的实时性，提升了稳定性，具有推广价值。

参考文献：

[1] 胡艺,杨帆,潘国峰. 一种改进的印刷电路板缺陷检测分割算法[J]. 科学技术与工程,2017,17(9):221-228.

[2] 王福斌,李迎燕,刘杰,等. 基于OpenCV的机器视觉图像处理技术实现[J]. 机械与电子,2010,28(6):54-57.

[3] 吴一全,樊军,吴诗婳. 改进的二维Otsu法阈值分割快速迭代算法[J]. 电子测量与仪器学报,2011,25(3):218-225.

[4] 刘金,金炜东.噪声图像的快速二维Otsu阈值分割[J].计算机应用研究,2013,30(10):3169-3171,3200.

[5] 李贤阳,黄婵. 一种结合改进Otsu法和改进遗传算法的图像分割方法[J]. 实验室研究与探索,2012,31(12):57-61,112.

[6] 吴昊,汪荣贵,方帅,等. 基于最小类内差和最大类间差的图像分割算法研究[J]. 工程图学学报,2011,32(1):67-75.