基于改进多分类概率SVM模型的变压器故障诊断

,,张作, ,

(1．广东电网有限责任公司惠州供电局，广东 惠州 516000；2.西安交通大学电气学院，陕西 西安 710049)

0 引言

电力变压器作为电力系统的关键设备，在电网中起到能量传输、分配的功能，其运行状况的健康与否直接关系到整个电网的安全性及稳定性。如未能及时发现电力变压器的潜在故障，未能及时安排相应的检修工作，往往会导致该变压器所管辖的供电区域大面积停电，造成巨额的经济损失[1-2]。因此，深入研究电力变压器的故障诊断，降低故障的发生率，避免事故的发生尤为重要。

大型电力变压器由于其内部结构的复杂性和故障的多样性，需要通过大量的试验进行变压器的状态评估[3]。其中，油中溶解气体分析(DGA)通过检测气体的组分和含量来分析设备的状态，不受外界电磁场的干扰，不影响变压器的正常运行，同时可实现实时在线监测及时发现内部潜伏故障，是检测电力变压器内部潜在故障的最主要手段之一，且在《电力设备预防性试验规程》中被列为首位[4]。

随着信息技术、人工智能、数据挖掘领域的发展，基于油色谱分析的诊断方法的研究从传统的三比值法、IEC三比值法、Rogers法、大卫三角形法等转变为专家系统、粗糙集算法、人工神经网络、支持向量机等智能信息处理算法[5-6]。其中，支持向量机基于结构风险最小化原则构建分类器，能够较好地解决小样本、高维度、非线性数据集的模式识别问题。文献[7]利用PCA和KICA对变压器油色谱数据进一步特征提取，并利用支持向量机取得良好的诊断效果。文献[8]运用多分类概率输出的方法，通过支持向量机得到发生不同类型故障的概率，进一步降低误诊断的发生。

在此，结合了油中溶解气体分析技术和优化多分类支持向量机，通过近邻算法优化多分类拓扑结构，降低模型复杂度及构建时间，再利用一对一(OVO)及优化后的一对多(OVR)结合的方式实现电力变压器多类故障诊断及概率输出。克服了原有单一多分类算法和传统诊断算法的不足，有效提高了诊断的准确率和结论的可靠性。

1 多分类概率输出支持向量机

1.1 SVM概率输出

在二分类问题中，支持向量机(SVM)利用核函数将低维度数据映射到高维空间，并基于结构风险最小化原则在高维空间内寻找最优分类超平面，ωTφ(x)+b=0，其中ω为权值向量，b为偏置量，尽可能地将2类样本分隔在超平面的两侧，使得分类的间距最大，提高分类器的抗干扰能力。SVM决策函数输出形式为：

(1)

x为输入的待分类样本；xi为训练集内的样本数据；y∈(-1,1)为对应训练集样本xi的标签值；ai为拉格朗日乘子；k(xi,x)为核函数；f(x)为决策函数输出的确定值。传统的支持向量机最终基于阶跃函数y=sign(f(x))，输出待分类样本的分类结果y。

在此，采用Platt[9]提出二分类SVM概率输出方法，利用Sigmoid函数将传统支持向量机的决策函数输出值f(x)映射到[0,1]区间内，输出待分类样本隶属概率值。具体概率输出式为：

P(y=1|x)≈PA,B(f(x))=

(2)

A，B为Sigmoid函数的待拟合参数，可以利用训练集样本的决策函数输出及标签值进行极大似然估计获取。定义训练集为(f(xi),ti)，求解模型为：

(3)

N+为训练集样本中标签为yi=+1的样本个数；N-为训练集样本中标签为yi=-1的样本个数。

求解上述模型最优解时，可以利用牛顿法，F(A,B)的梯度矩阵和Hessian矩阵分别为：

(4)

H(F)=

(5)

获取参数A,B值之后，即可通过概率输出式求解待分类样本隶属于某一类的概率估计值。

1.2 多分类SVM

SVM分类器最初的设计就是为了解决二分类问题，当处理多类问题时，需要构造合适的多类分类器。目前，构建多分类SVM主要通过组合多个二分类SVM来实现多类分类器的功能，常用的方法有OVR(one-versus-rest)和OVO(one-versus-one)2种[10]。

OVR是通过将多个类别转化为2类实现多分类功能。假设有K种不同类别的样本集，只需要训练K个二分类SVM。构造每个二分类SVM时，将其中某个类别的样本标记为一类，将剩余的其他样本都归为另一类。测试未知样本时，结合概率输出，获取该样本属于各类的概率值，选取概率最大的类别作为输出。

ClassOVR=argmaxi=1,…,kpi

(6)

OVO是通过每2类构成1个SVM子分类器实现多分类功能。同样假设有K种不同的类别，两两训练，一共得到K×(K-1)/2个SVM子分类器。测试未知样本时，结合概率输出，每个SVM子分类器都能输出该样本隶属各类的概率，得到1个K阶的概率矩阵G：

(7)

rij代表待测试样本在第i类和第j类构成的二分类SVM中，隶属于第i类的概率值；rij∈[0,1]，rij+rji=1。最后利用加权投票策略，输出的样本类别为：

ClassOVO=argmaxi=1,…,k∑1≤j≠i≤krij

(8)

2 改进多分类概率SVM模型

2.1 KNN算法

近邻算法(KNN)是由Cover等人提出的一种基于不同对象间的特征值距离对目标对象进行有效分类的非参数估计算法[11-13]。其核心思想是：同类样本拥有相同的特征往往会表征出相似的数据结果，因此通过计算未知样本与已知样本之间的特征向量相似度，选取k个相似度最接近的已知样本，依据其中占优的类别，即可对未知样本进行类别的判定。算法具体流程如下：

a.输入未知样本类别的数据集(记为测试集)及已知样本类别的数据集(记为训练集)，假设测试集有M个样本数据，训练集有N个样本数据。

b.分别计算测试集未知样本与训练集已知样本之间的特征向量相似度，得到一个N×M的相似度矩阵。其中，每列代表某个未知样本与所有已知样本的相似度向量。

c.每列相似度向量均按相似度的递减关系进行排序。

d.根据相似度数值分布及样本特性选定合适的k值。

e.依据排序结果，按列选取前k个最大相似度对应的已知样本，即每个未知样本对应k个相似度最大的已知样本。

f.统计每个未知样本的k个已知样本所处类别的出现次数。

g.按列返回前k个已知样本中出现频率最高的类别，得到M维行向量，其中的元素代表着对应未知样本的判定类别。

2.2 多分类策略

OVO-SVMs分类器通过对概率矩阵G的每行元素进行相加，获得的累加值来表征样本属于各类的程度，选取最大累计值对应的类别作为样本输出类别。其中，每个元素rij代表待测试样本在第i类和第j类构成的二分类SVM中，隶属于第i类的概率值。假设一个样本属于第c类(c≠i≠j)，将其作为OVO-SVMs分类器的输入进行类别判定，得到的概率矩阵中，rij的数值是没有任何意义，因为样本本身就不属于i，j类。理想情况下，期望得到rij≈0.5，这表明该样本在第i类和第j类构成的二分类SVM中分类不明确，得到该样本既不属于第i类，也不属于第j类的结论。但是实际上，rij的值是多变的，并不会一直保持在0.5的邻域中，而它的结果会累加在最终的类别判定式(8)中，造成错误的输出。因此，期望对概率矩阵中的每个元素乘上一个权重系数qij来修正输出的概率值，从而减少上述中的误分类情况，提高OVO-SVMs分类器的分类准确率。理想情况下，若样本类别属于第i类或第j类，qij≈1，否则qij≈0。由于事先并不能得知样本的真实类别，所以采用qij=max(qi,qj)来估计未知样本属于第i类或第j类的概率，此时输出的样本类别为：

ClassOVO-OVR=argmaxi=1,…,k∑1≤j≠i≤krij·qij

(9)

qij=max(qi,qj)

(10)

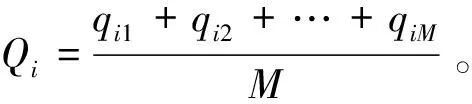
ClassOVO-impOVR=argmaxi=1,…,k∑1≤j≠i≤krij·Qij

(11)

Qij=max(Qi,Qj)

(12)

Qi为第i类与其他所有类构成的改进OVR-SVMs分类器的概率输出。

2.3 改进多分类概率SVM模型

运用改进多分类方法对K种不同类别的样本集进行识别分类，需要构造K×(K-1)/2个OVO-SVMs及K×M个OVR-SVMs。而电力变压器的故障涉及面广且类型较多，如果将所有故障一并作为输入进行训练，需要构造大量的SVM，花费大量的训练时间及测试时间。因此，首先采用有向无环图，对变压器的故障进行归类划分，具体划分如图1所示。

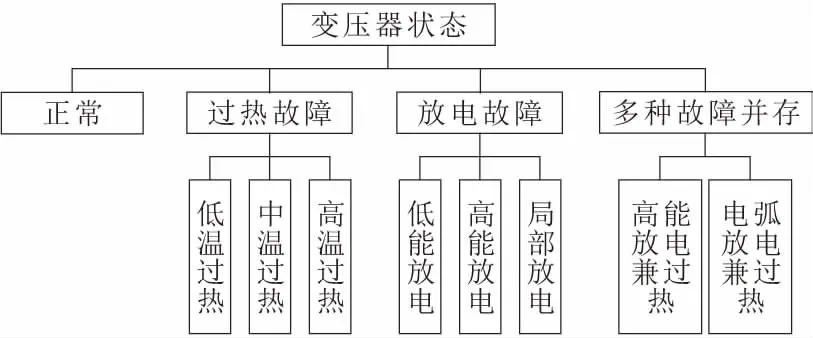
图1 变压器故障结构树

变压器状态大体分成正常、过热、放电、多故障并存4个大类，针对不同的大类再进行子故障的细分。在此，采用KNN算法对变压器故障的4个大类进行初步划分，选取近邻中出现频率较高的2类，再利用改进多分类方法对2个大类下的所有子故障进行多类别细分，输出隶属各子故障的概率。经过KNN算法预分类，筛选去除部分故障大类，大大减少构建多分类器的时间，同时规避了多分类器出现误诊的风险，提高了多分类器分类的准确率及稳定性。

由于电力变压器众多物理和化学检测手段中，油中溶解气体分析通过分析气体的组分和含量来检测设备状态，能够较好地反映出变压器故障性质及恶劣程度，及时发现内部潜伏故障。因此，采用变压器油色谱数据作为模型的输入，根据油中气体组分含量，进行变压器故障诊断。由于油中特征气体含量大小差异过大，为了减少模型的计算难度及误差，首先对输入数据进行如下归一化处理：

(13)

xgyh代表归一化后气体含量；x代表色谱分析检测到的气体真实含量；xmin代表气体含量的最小值；xmax代表气体含量的最大值；Llow为设定的气体含量归一化后的下界；Lup为设定的气体含量归一化后的上界。为了方便计算，设定Llow=0，Lup=1，此时xgyh∈[0,1]。具体诊断流程如图2所示。

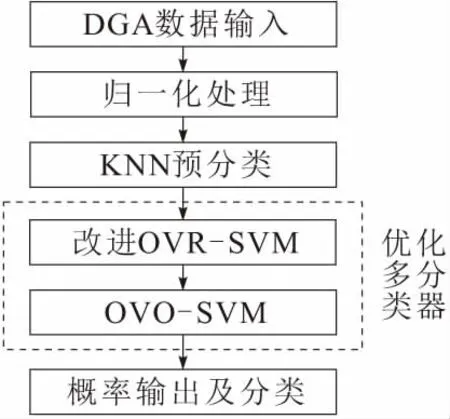
图2 变压器故障诊断流程

3 试验结果与分析

本文从中国南方电网某市供电局中收集得到226组带标签的变压器油色谱数据，其中包含186组8种典型故障，各类故障的样本数如表1所示。由于获取的变压器各类故障样本数较少，按照训练集样本数比测试集样本数等于1∶1的标准，分别从每个类别中选取一定数量的训练集样本及测试集样本，用于构建OVO-SVMs及改进的OVR-SVMs模型。整合所有训练集作为KNN的已知样本集。同时，选取油中溶解的H2，CH4，C2H6，C2H4和C2H2作为气体特征参数，对每个测试集样本进行逐一分类，并比较IEC三比值法、OVO-SVMs多分类法及本文提出的多分类方法的诊断结果。

表1 变压器故障样本集

在KNN算法预分类的过程中，设定K=12，预选取出现频率最大的2类故障。如果样本的真实故障类别属于KNN算法预分类结果的2种故障大类，则判定KNN算法有效地剔除了无关故障类，克服后续模型诊断耗时长、高复杂的缺点，起到辅助诊断的作用，那么认为KNN算法分类结果正确。KNN算法的预分类结果如表2所示。KNN算法对于故障和正常的分类达到100%的效果，对各大类故障也都有较高的识别率。

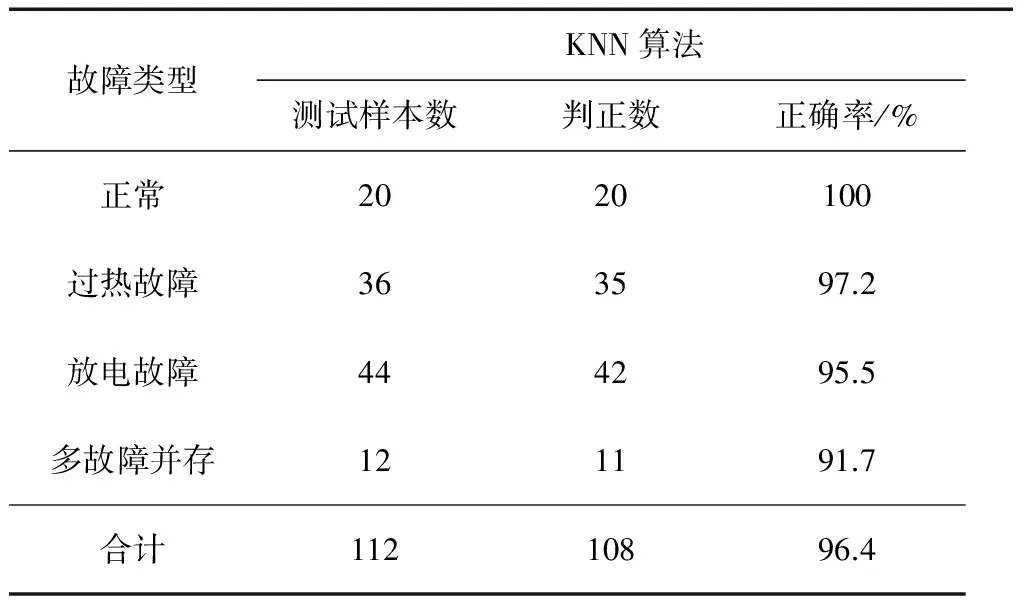
表2 KNN算法的预分类结果

本文选取径向基函数作为支持向量机的核函数，其中核函数参数及惩罚因子的整定，通过网格搜索法[1],对训练集中的样本进行留一交叉验证，选取准确率最高的一组参数。核函数参数取值范围为10-3,10-2,…,102,103；惩罚因子取值范围为10-3,10-2,…,102,103。测试集样本在IEC三比值法、OVO-SVMs和本文方法3种不同方法下的变压器故障诊断结果比较，如表3所示，其中包含各种子故障的判正数及正确率。

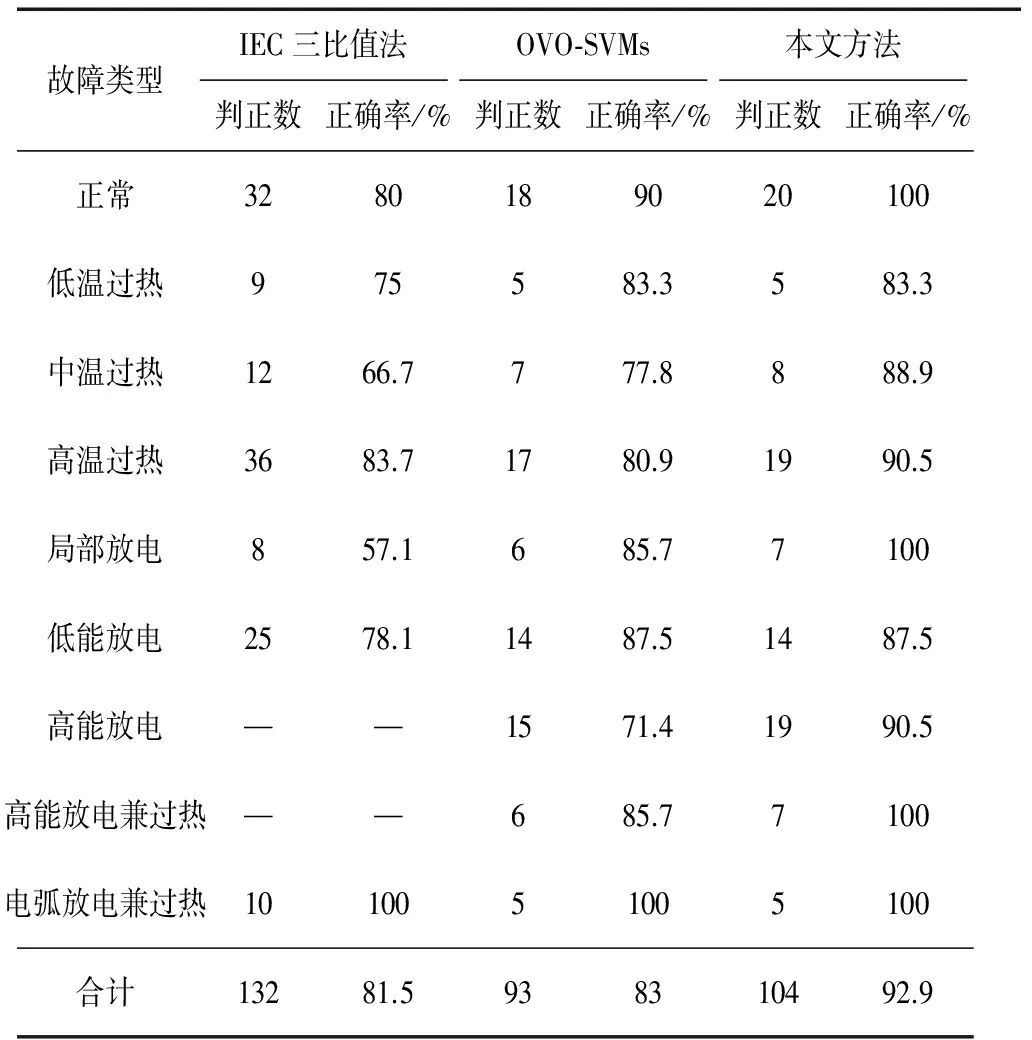
表3 IEC三比值法、OVO-SVMs和本文方法的

注：“—”代表IEC三比值法无法识别该故障类型。由于OVO-SVMs和本文方法需要总数据集的一半作为训练集，所以测试集样本仅有IEC三比值法的测试样本的半数。

由表3可知，相比较其他2种方法，本文提出的近邻与改进多分类结合的方法整体诊断效果最佳。与IEC三比值法相比，本文的方法不但在多个子故障的分类正确率方面有所提高，而且不受编码和故障类型的限制。

基于3种不同方法的变压器故障诊断的相关案例，如表4所示。表4中，IEC三比值法无法对“0,1,1”的编码有效识别，而本文方法能够正确地识别及诊断该故障类型。同时，相比IEC三比值法无法对高能放电进行识别，本文方法却对高能量放电及高能放电兼过热这2种故障的诊断效果良好，诊断正确率分别达到90.5%和100%。

与传统的OVO-SVMs对比，本文利用改进OVR算法的输出对概率矩阵G的每个元素进行修正处理，强化与样本故障类别相关的分类器的概率输出结果，对其余分类器输出结果进行弱化处理，进一步提高了诊断准确率。

除此之外，以本文的9个故障类别(含正常状态)为例，针对每个未知样本的诊断，改进多分类算法需要经过45个SVM进行分类，而引入KNN算法进行预分类后，最多需要21个SVM进行识别，最少只需6个SVM即可完成诊断工作，大幅度提高变压器故障诊断的效率。

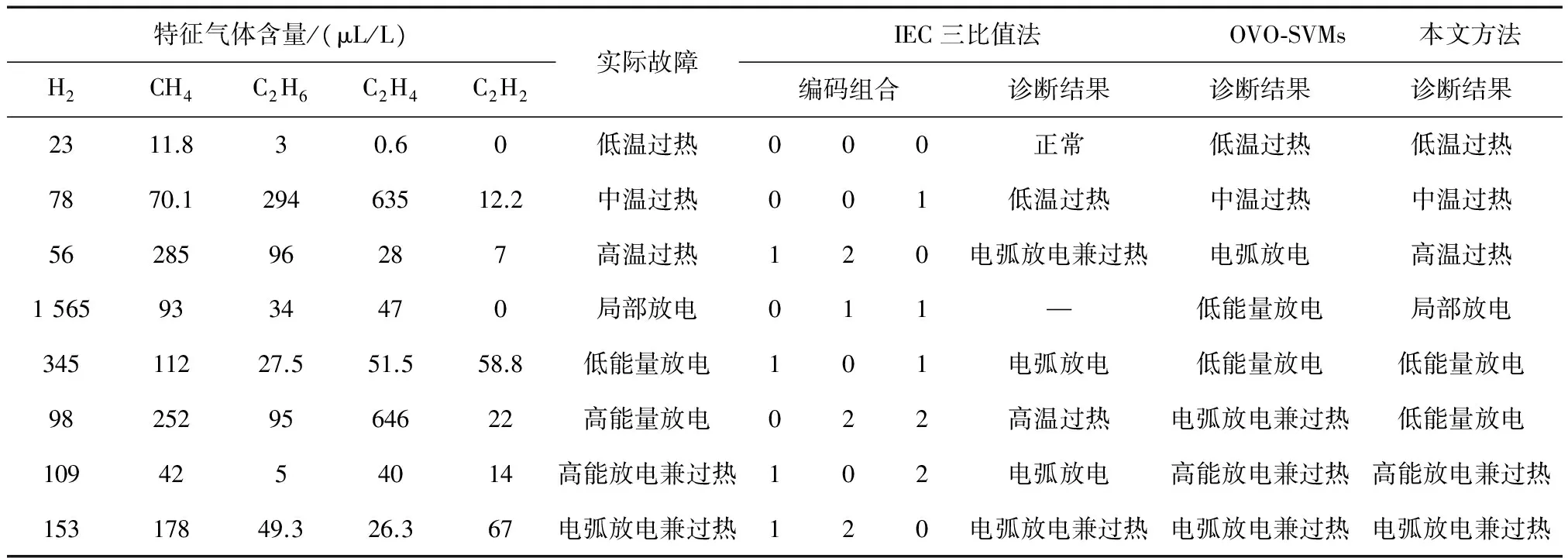
表4 IEC三比值法、OVO-SVMs和本文方法的变压器故障诊断实例

注：“—”代表IEC三比值法无法识别该编码。

4 结束语

结合KNN算法和多分类策略结合的方法对变压器故障进行诊断：以OVO-SVMs分类器为基础，克服了IEC三比值法存在编码缺失等问题，补充了对高能放电和高能放电兼过热2种故障的诊断；以改进OVR-SVMs分类器的概率输出作为概率矩阵G中各元素的权重系数，对概率矩阵G进行更新、修正，合理剔除无关类别训练成的支持向量机的概率输出，保留有效支持向量机的概率输出，提高故障诊断正确率及可靠性；考虑到针对变压器油色谱在线监测系统的故障诊断实时性，采用有向无环图的形式先对变压器故障进行归类，再利用KNN算法对故障大类进行预分类，缩小故障所属类别，降低了诊断模型的复杂性，提高了改进多分类算法的运算速率，整体诊断速率可提高2～9倍。从整体诊断效果来看，本文提出的方法与IEC三比值法和传统的多分类支持向量机相比，在故障诊断范围、故障诊断正确率以及故障诊断效率上均有所提高。

参考文献：

[1] 张东波,徐瑜,王耀南.主动差异学习神经网络集成方法在变压器DGA故障诊断中的应用[J].中国电机工程学报,2010,30(22):64-70.

[2] Yang Q, Su P, Chen Y.Comparison of impulse wave and sweep frequency response analysis methods for diagnosis of transformer winding faults [J].Energies,2017,10(4):431.

[3] 潘翀，陈伟根，云玉新，等．基于遗传算法进化小波神经网络的电力变压器故障诊断[J].电力系统自动化,2007,31(13):88-92．

[4] 郭创新,朱承治,张琳,等．应用多分类多核学习支持向量机的变压器故障诊断方法[J]．中国电机工程学报,2010,30(13):128-134．

[5] 郑蕊蕊,赵继印,赵婷婷,等．基于遗传支持向量机和灰色人工免疫算法的电力变压器故障诊断[J]．中国电机工程学报,2011,31(7):56-63．

[6] 胡青,孙才新,杜林,等．核主成分分析与随机森林相结合的变压器故障诊断方法[J]．高电压技术,2010,36(7):1725-1729.

[7] 唐勇波,桂卫华,彭涛,等.PCA和KICA特征提取的变压器故障诊断模型[J].高电压技术,2014,40(2):557-563.

[8] 毕建权,鹿鸣明,郭创新,等.一种基于多分类概率输出的变压器故障诊断方法[J].电力系统自动化,2015,39(5):88-93.

[9] Platt J．Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods [J]．Advances in Large Margin Classifiers,1999,10(3):61-74．

[10] Chmielnicki W, Stapor K. Using the one-versus-rest strategy with samples balancing to improve pairwise coupling classification[J]. International Journal of Applied Mathematics and Computer Science, 2016,26(1):191-201.

[11] 刘凡,张昀,姚晓,等.基于K近邻算法的换流变压器局部放电模式识别[J].电力自动化设备,2013,33(5):89-93.

[12] Galar M, Fernández A, Barrenechea E, et al.Dynamic classifier selection for one-vs-one strategy: avoiding non-competent classifiers[J]. Pattern Recognition, 2013, 46(12): 3412-3424.

[13] 田质广,张慧芬．基于遗传聚类算法的油中溶解气体分析电力变压器故障诊断[J]．电力自动化设备,2008,28(2):15-18．