一种基于置换的组合分类器剪枝方法

，

(信阳师范学院，河南 信阳 464000)

在过去的十几年里，组合分类方法研究一直是机器学习和数据挖掘中热门的研究领域。给定相同的训练信息，组合分类器往往比单个分类器表现出更好的泛化能力，这是因为其创建有差异且具备高准确率的基分类器。

构建有差异且具备高准确率组合分类器的方法有很多。例如，通过抽样为每个基分类器构建有差异的训练集；通过操纵特征基将训练集映射到不同的特征空间，进而为基分类器构建不同的训练集(如COPEN[1])；通过操纵算法的参数或结构从而构建准确且有差异的组合分类器。

然而，大部分组合分类器的方法存在一个共同的问题：倾向于构建大量的基分类器，这样不但需要大量的存储空间，而且增加了组合分类器的预测响应时间。在一些实际应用(如数据流)中，最小化运行时间是至关重要的。组合剪枝(组合选择，组合瘦身)是处理该问题的一种有效方法，即选择全部基分类器的一个子集作为子组合分类器，用于预测未知样例[2-6]。

本文将置换策略引入组合分类器剪枝问题中，进而提出了基于基分类器置换的组合分类器剪枝方法(EPR，Ensemble Pruning via base-classifier Replacement)。同时，使用差异性方法分析了EPR的性质，基于该性质，提出了一种基于差异性的度量指标(Diversity-based Measure)以评估分类器相对于组合分类器的重要性，进而用该度量指标指导EPR搜索最优或次优目标。

1 问题定义及算法基本思想

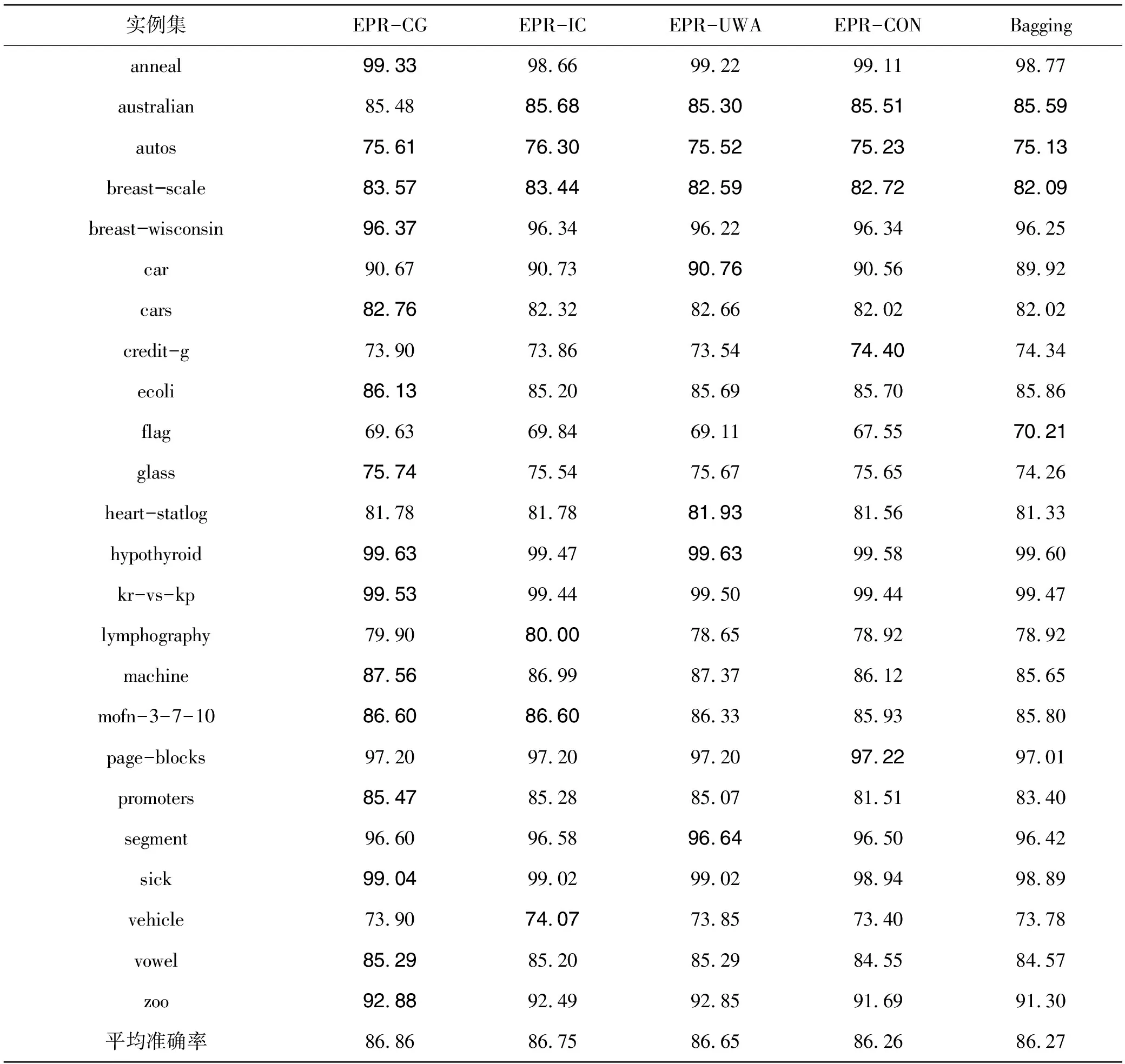
设H={h1,h2,…,hM}是一个包含M个成员的组合分类器，所要考虑的问题是：如何从H中选择子组合分类器S，使得|S|<

本文使用基于置换策略的贪心方法剪枝组合分类器。用H中的成员初始化子组合分类器S为预定义大小，然后迭代地用较好的基分类器置换S中最差的基分类器，直到置换不能进行，其核心是设计有效的度量指标评估一个分类器相对于组合分类器的重要性。

2 EPR的相关性质分析

本文采用由Ho提出的0/1差异性度量(0/1 loss-based disagreement measure)描述组合分类器成员间的配对差异性。其具体定义如下：

(1)

其中，N是实例集D的大小。

由定义1可知，分类器hi和hj间的差异性实质上是hi和hj有且仅有一个分类器正确分类实例集D中的实例比例。

定义2 给定实例集D，分类器h对组合分类器S的差异性贡献定义为h与S中所有的分类器差异性之和，即

(2)

定理1 定义2中分类器h对组合分类器S的差异性贡献值也可写为

(3)

定义3 组合分类器S的差异性(DivD(S))为S中每个分类器差异性贡献之和，即

(4)

引理1 设h′S是一个基分类器，S′=S{h}∪{h′}是一个组合分类器，即：S′是由h′置换S中的h获得的。如果ConDivD(h′,S′)>ConDivD(h,S)，那么，S′比S更优越，即：DivD(S′) >DivD(S)。

其中,

(5)

类似地，我们可以证明

(6)

由S′=S{h}∪{h′}得

S′{h′}=S{h},S′{h′,hj}=S{h,hj}

(7)

组合式(5)、式(6)和式(7)得

DivD(S′)-DivD(S)=2(ConDivD(h′,S′)-

ConDivD(h,S))

(8)

故，Div(S′)>Div(S)如果ConDivD(h′,S′) >ConDivD(h,S)。

定理2 设h′∉S是一个基分类器，设S′=S{h}∪{h′}是一个组合分类器，即：S′是由h′置换S中的分类器h获得。那么，式(9)成立

DivD(S′)∝ConDivD(h′,S{h})-ConDivD(h,S{h})

(9)

证明：由引理1中的等式(8)得

DivD(S′)=

DivD(S)+2(ConDivD(h′,S′)-ConDivD(h,S))=

DivD(S)+2(ConDivD(h′,S′{h})-

ConDivD(h,S{h}))

(10)

由式(10)和已知条件S′=S{h}∪{h′}可以看出，式(9)成立。

定理2表明，在空间{S′|S′=S{h}∪{h′},h∈S}中搜索具有最大差异性的最优子组合分类器S′，等价于在S中搜索分类器h∈S，使得式(9)右项最大。还可用式(11)选择候选分类器h作为被h′置换的对象,以确保DivD(S′)最大。如果h=h′，则置换不会发生。

(11)

3 基于差异的度量指标

根据定理1和定理2，这里设计了一个基于差异的度量指标。根据定理2和式(11)，定义h被h′置换时的贡献增益(Contribution Gain，CG)为

CGDpr(h′,h)=ConDpr(h′,S{h})-ConDpr(h,S{h})

(12)

其中，Dpr为剪枝集;ConDpr(h,S)表示基分类器h对组合分类器S的贡献，定义为

(13)

EPR用式(14)选择分类器h作为候选被h′置换，如果h=h′，则置换不发生，其中式(14)是由式(11)和(12)演化而来的。

(14)

4 实 验

4.1 数据集及实验设置

从UCI数据库中随机选取24个实例集，它们的细节描述见表1。对于每个实例集，执行一次10折交叉验证：将每个实例集随机地划分为10个不相交的子集。对于每个子集，其他9个子集被当作训练集，该子集用来测试集评估算法的性能。对于每次试验，使用bagging建立包含200个基分类器的分类器库，其中，基分类器由剪枝C4.5建立。

本文设计了2组实验：第一组实验评估CG的性能；第二组实验评估EPR的性能。对于第一组实验，选择CG、IC[7]、UWA[8]以及COM[9]监督EPR的搜索过程(分别表示为EPR-CG、EPR-IC、EPR-UWA以及EPR-COM)。对于第二组实验，将EPR与基于向前选择和向后移除的组合分类器剪枝方法相比较，其中，CG和IC被选为候选指标监督搜索过程。为了便于说明，令F-*(B-*)表示向前(向后)组合分类器剪枝方法，其中“*”表示度量指标。例如，F-CG(B-CG)表示使用度量指标CG监督向前(向后)组合分类器剪枝方法。

4.2 实验结果

4.2.1 第一组实验

本实验分析了指标CG的性能。相关的结果如表2所示，其中，粗体表示相应的算法在相应的实例集上准确率最高。为了清晰，表2省略了算法在相应实例集上的标准差。作为参照，表2给出了bagging(分类器库)的准确率。

表1 24个实例集的具体信息描述

由表2可知：

(1)EPR-CG可以大幅度降低组合分类器的规模，并能有效地提高原组合分类器性能(本实验有20个实例集显著提高了组合分类器的准确率)；

(2)相比于其他指标，CG更适合监督EPR剪枝的过程。具体地，EPR-CG在绝大部分实例集上较高的准确率数为14个，其他依次是EPR-IC 5个、EPR-UWA 5个、EPR-CON 2个和bagging 1个。它们的平均准确率分别为86.86%、86.75%、86.65%、86.26%和86.27%。EPR总体上能有效地提高组合分类器的分类准确率。

表 2 算法在24个实例集的平均准确率

根据文献[9]，当比较两个或多个算法时,比较它们在每个实例集上的序(rank)以及在所有实例集上的平均序(average rank across all data sets)。在一个实例集上，准确率最高的分类器的序为1.0，准确率次高的分类器的序为2.0，以此类推。算法在每个实例上的序如表3所示。

表3的内容进一步证实了上面的结论，即EPR方法能有效地提高组合分类器的性能；较之于其他度量标准，CG更适于监督EPR剪枝组合分类器。具体情况是，EPR-CG以1.75的平均序排名第一位，紧随其后的算法依次是EPR-IC，EPR-UWA和EPR-CON，它们的平均序分别为2.71，2.73和3.60，Bagging以4.08的平均序落到了最后一位。

4.2.2 第二组实验

本实验比较了EPR与向前、向后组合分类器剪枝算法性能，使用度量指标CG与IC作为代表，监督EPR搜索子组合分类器空间。相关结果如表4和表5所示，其中，表4为EPR-CG、F-CG和B-CG在每个实例集上平均准确率和序，表5为EPR-IC、F-IC

表3 算法在每个实例集上的序

和B-IC在每个实例集上的平均准确率和序。粗体表示相应算法在相应实例集上具有最高的准确率。

直觉上，EPR-*、F-*及B-*性能相当，因为这些剪枝方法的思想类似(都是贪心组合分类器剪枝方法)。事实上，表4和表5结果验证了该直觉：不管度量指标是CG还是IC，这3种算法在每个实例集上准确率差异都较小。

从表4和表5还可以看出，尽管这几种方法准确率差异不大，但是，在大部分实例集上，EPR算法略优于其他2种算法。当CG作为度量指标时，EPR在19个实例集上准确率较高，其他依次是F-CG为9个和B-CG为6个，它们的平均序为：EPR-CG 为1.44、F-CG为2.27和B-CG为2.29。在表4中，EPR-IC在18个实例集上准确率较高，其他依次是F-IC为 7个和B-IC为5个。它们的平均序为：EPR-IC为1.46、B-IC为2.21和F-IC为2.33。该结果表明，相比于其他高级组合分类器剪枝方法，EPR能寻找到准确率更高的子组合分类器。

另外，仔细观察表4和表5可知，基于向前选择的组合分类器剪枝方法与基于向后移除的组合分类器剪枝方法性能相当。

综上说述：

(1)不管采用上述哪种指标监督EPR搜索过程，EPR总能显著降低组合分类器规模并有效提高它的泛化能力；

表 4 算法EPR-CG、F-CG和B-CG在每个实例集上的平均准确率和序

表5 算法EPR-IC、F-IC和B-IC在每个实例集上的平均准确率和序

(2)本文设计的基于差异性的指标较适于监督EPR搜索过程；

(3)较之于其他高级组合分类器剪枝方法，EPR略显优势。

5 结 语

本文提出了一种EPR组合分类器剪枝方法。它利用置换方法搜索最优或次优子组合分类器。为了评估基分类器对组合分类器的贡献，使用差异性度量理论分析了EPR的性质，根据该性质，设计了一个基于差异性的度量指标，监督EPR搜索子组合分类空间。

有很多指标可用于监督组合分类器剪枝过程，因此将这些指标用于指导EPR搜索子组合分类器是未来值得研究的一项工作。

参考文献:

[1] Zhang D, Chen S, Zhou Z H,et al.Constraint Projections for Ensemble Learning[C]//Proceedings of the 23rd AAAI Conference on Artificial Intelligence (AAAI’08).Quebec:AAAI Press，2008: 758-763.

[2] Partalas I, Tsoumakas G, Vlahavas I P.An Ensemble Pruning Primer[C]//Applications of Supervised and Unsupervised Ensemble Methods.Berlin: Springer, 2009: 1-13.

[3] Li N, Yu Y, Zhou Z H.Diversity Regularized Ensemble Pruning[C]//Flach P A , Bie T D, Cristianini N, et al.Proceedings of European Conference on Machine Learning and Knowledge Discovery in Databases.Berlin:Springer, 2012: 330-345.

[4] Tamon C, Xiang J.On the Boosting Pruning Problem[C]//Proceedings of the 11th European Conference on Machine Learning.Berlin:Springer, 2000: 404-412.

[5] Xu L L, Li B, Chen E H.Ensemble Pruning via Constrained Eigen-Optimization[C]//Proceedings of the 12th IEEE International Conference on Data Mining.Los Alamitos:IEEE Press, 2012: 715-724.

[6] Guo L, Boukir S.Margin-based Ordered Aggregation for Ensemble Pruning[J].Pattern Recognition Letters, 2013, 34: 603-609.

[7] Lu Z, Wu X D, Zhu X Q, et al.Ensemble Pruning Via Individual Contribution Ordering[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.NY:ACM New York, 2010: 871-880.

[8] Partalas I, Tsoumakas G, Vlahavas I P.An Ensemble Uncertainty Aware Measure for Directed Hill Climbing Ensemble Pruning[J].Machine Learning, 2010, 81(3): 257—282.

[9] Banfield R E, Hall L O, Bowyer K W, et al.Ensemble Diversity Measures and Their Application to Thinning[J].Information Fusion, 2005, 6(1): 49-62.

[10] Demsar J.Statistical Comparisons of Classers over Multiple Data Sets[J].Journal of Machine Learning Research, 2006(7): 1-30.